在这项工作中，我通过创建一个包含四只基金的模型来探索 copula，这些基金跟踪股票、债券、美元和商品的市场指数。
然后，我使用该模型生成模拟值，并使用实际收益和模拟收益来测试模型投资组合的性能，以计算风险价值(VaR)与期望损失(ES)。
一、介绍与概述
Copulas函数确实是对多元分布中变量之间的相关性进行建模的有效工具。这种函数能够将多变量依赖关系与单变量边缘分布相结合，使得我们能够更灵活地处理多变量数据。Copulas函数允许我们单独对构成多变量数据的每个变量使用单变量模型，然后再将这些模型组合起来以描述整个多元分布。
Copulas函数最早由数学家、经济学家和金融工程师David X. Li在2000年提出，并自那时起开始逐渐流行。其理论基础是Sklar定理，它表明任何一个多变量之间的关联关系都对应着一个用于表示这种关系的函数，即Copula函数。这使得Copula函数成为表示多变量之间全部关联关系的统一工具。
可下载资源
作者
根据 Salmon (2009) 的说法，Li (2000) 最近提出的Copulas应用之一是 2008 年开始的金融危机。
我们将使用 copulas 来模拟四个 ETF 基金的行为：IVV，跟踪标准普尔 500 指数；TLT，跟踪长期国债；UUP，追踪外汇指数；以及商品的 DBC。
二、理论背景
copula 是一个多变量 CDF，其边缘分布都是 Uniform (0,1)。假设 Y 有 d 维，并且有一个多元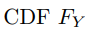 
和边缘 
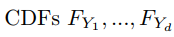。很容易证明，每个
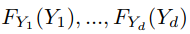都是 Uniform(0,1)。因此，
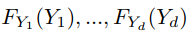的 CDF 根据定义是一个 copula。使用 Sklar (1973) 的定理，然后我们可以将我们的随机变量 Y 分解为一个 copula CY ，它包含关于我们的变量 Y 之间相互依赖的信息，以及单变量边缘 CDFs FY ，它包含关于每个变量的所有信息单变量边缘分布。对于 d 维，我们有：
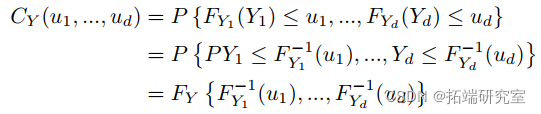
并使每个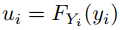
，我们有：
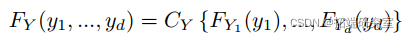
如果我们对等式（2）进行微分，我们会发现 Y 的密度为：
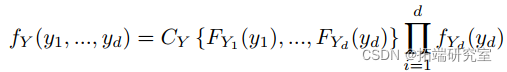
方程 (3) 中的结果允许我们创建多变量模型，这些模型考虑了变量的相互依赖性（方程的第一部分）和每个变量的分布（方程的第二部分）。我们可以使用 copula 和边缘部分的参数版本来创建可用于运行测试和执行预测的模型。在接下来的几节中，我们将使用用于统计计算的 R 语言将高斯和 t-copula 拟合到介绍中描述的 ETF 的对数收益率。有了 copula 和边缘，我们将使用模型来确定投资的风险价值 (VaR) 和预期损失 (ES)。
三、算法实现与开发
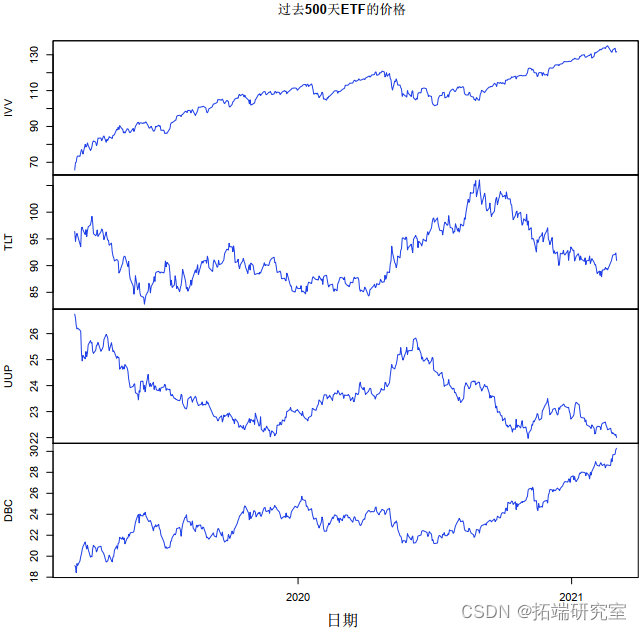
像往常一样，我们从读取文件开始。图 1 显示了价格图：注意 IVV 和 DBC（股票和商品）之间的关系以及 TLT 和 UUP（元和国债）之间的关系。
# 将 ETF 读入
read.zoo("F.csv")
# 获取最近501天
tf\[(T-500):T,\]
# 绘制价格
pdf("价格.pdf")
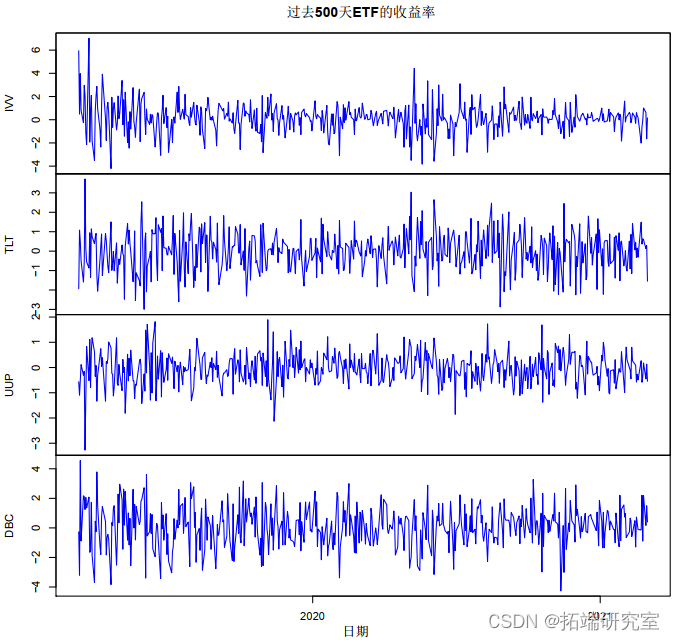
在这种情况下，我们计算对数收益率。图 2 显示了收益图。
# 计算对数收益 le <- lag(e，-1 log(ef) - log(lef) ) * 100
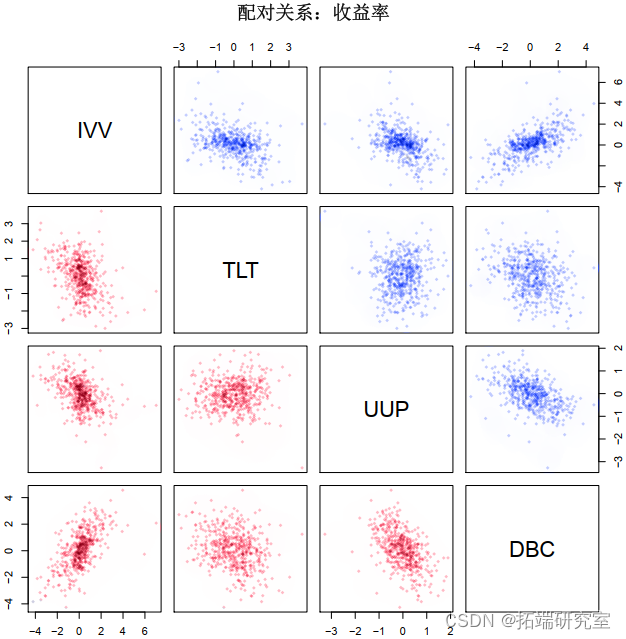
然后我们做一个配对图来确定结果是否相关，例如，正如期望的那样，IVV 和 DBC 之间存在非常高的相关性。图 3 显示了配对图。然后我们获得边距的参数，拟合每个变量的分布。结果见表一
# 拟合分布 fitdr ## 得到结果矩阵 # 将 AIC 函数应用于第一项（值） # params 列表的第四项 (loglik) AIC(saply (saply(prms, 4)) # params 列表的第一项（估计） sapply (sapply(pams,3))
随时关注您喜欢的主题
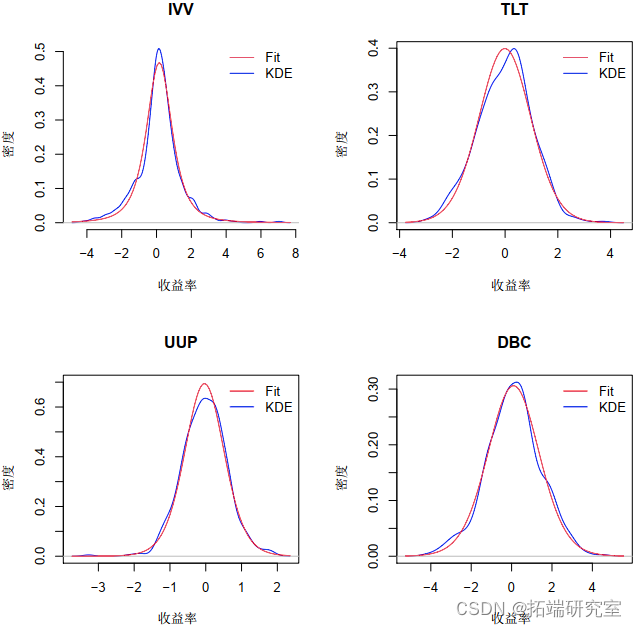
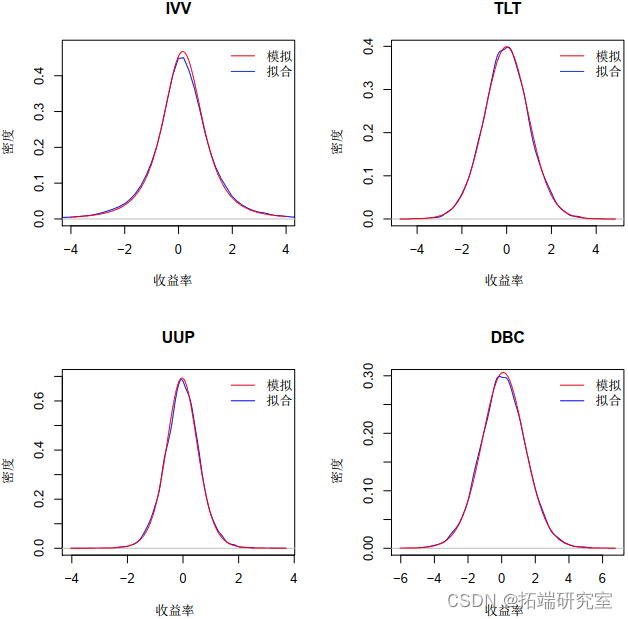
图 4 显示了拟合分布与来自变量的真实数据进行比较的图。现在我们有了边缘分布，我们需要找到模型的 copula。我们首先使用概率变换并获得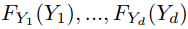 
中的每一个，我们知道它们是 Uniform(0,1)。这是通过以下代码完成的：
# 现在我们需要均匀分布 IV <- pct(IVV, a) rt <- cbind(uV uL, UP, DC)
图 5 显示了均匀分布之间的相关性。通过均匀分布，我们可以看到哪种类型的参数 copula 最适合。我们将拟合高斯 copula 和 t-copula，记录它们的 AIC 并查看哪一个提供了最佳拟合。
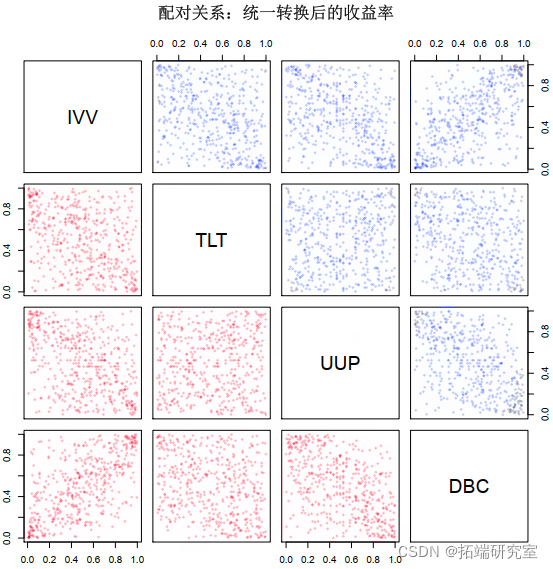
图 5：均匀分布之间的相关性
# 拟合高斯 copula fit.gaussian <- fitCopula (ncp)) # 记录拟合的AIC fit.aic = AIC(filik, ############################################### ############ # 现在是 t-copula fitCopula (tcop, url00)) # 记录拟合的AIC
AIC(fiik length(fite)
比较两种拟合，如表 II 所示，我们发现 t-copula 拟合最好，因此我们将根据 t-copula 的参数创建一个模型。然后，我们使用该模型生成 10,000 个观察结果，模拟我们模型的可能结果。
我们的模拟模型与拟合模型之间的图形比较可以在图 6 中看到 – 模拟非常接近拟合模型。
tCopula(parun") cop.dist <- mvdc(copt, parast1) rmvdc(co00)
现在我们有了模拟的观察结果，我们将使用参数方法计算风险价值 (VaR) 和预期损失 (ES)。我们将假设一个投资组合（任意选择）在 IVV 中投资 30%，在 TLT 中投资 15%，在 UUP 中投资 35%，在 DBC 中投资 20%。为了计算投资组合 w 的收益率 Rp，我们简单地使用矩阵代数将我们的模拟收益率 Rs 乘以权重，如 Rp = Rs × w。然后我们将 t 分布拟合到 Rp 并使用它来估计 VaR 和 ES。对于 t 分布，VaR 和 ES 的公式为：
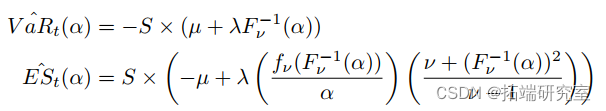
R中公式的应用实现如下。请注意，在代码中，VaR 和 ES 被四舍五入到最接近的千位。结果在表III中。
其中：
• S：仓位大小
• F -1 ν：逆 CDF 函数
• fν：密度函数 • µ：平均值
• λ：形状/尺度参数
• ν：自由度
• α：置信水平
# 计算模拟值的 VaR 和 ES fitdistr(re, "t") es <- -m+lada\*es1\*es2
我们的最终任务是计算非参数 ES 和 VaR，由以下公式给出：
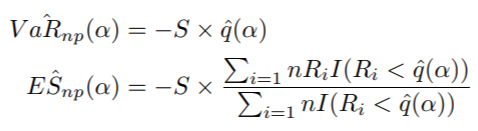
其中：
• S：仓位大小
• qˆ(α)：样本收益率的分位数
• Ri：第 i 个样本收益率
R 实现如下：
# 计算真实值的 VaR 和 ES ret <- (rf %*% w) / 100 ES <- -S * sum(ret * ir) / sum (iar)
结果示于表III中。
四、计算结果
表 I 显示了 ETF 边缘 t 分布的估计参数和 AIC 的结果：
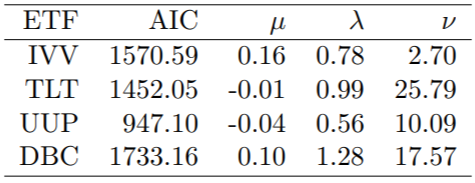
表 I 边缘分布
两个 copula 拟合的 AIC 都在表 II 中。
表 II Copula AIC
VaR 和 ES 在表 III 中。
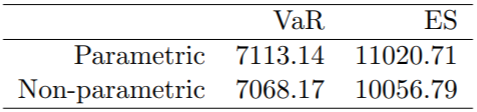
表三 VaR 和 ES
五、总结与结论
这项工作展示了如何估计边缘和 copula，以及如何应用 copula 来创建一个模型，该模型将考虑变量之间的相互依赖性。它还展示了如何计算风险价值 (VaR) 和期望损失 (ES)。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言VAR模型的多行业关联与溢出效应可视化分析
马尔可夫转换MSVAR模型预测资产收益率时间序列可视化分析|附数据代码
python中Copula在多元联合分布建模可视化2实例合集|附数据代码
R语言平稳性ADF检验、ARCH-LM效应检验分析收盘价收益率数据可视化
