假设你做了一个简单的回归…
现在你有了你的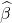 
. 您想知道它是否与（例如）零显着不同。一般来说，人们会查看他们选择的软件报告的统计数据或 p.value。
问题是，这个 p.value 计算依赖于因变量的分布。如果没有不同的说明，您的软件假定为正态分布，那是怎么回事？
可下载资源
例如，（95%）置信区间是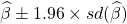 
,1.96 来自正态分布。
建议不要这样做，bootstrapping* 的优点在于它没有分布的问题，它适用于高斯、柯西或其他的分布。
40年前电脑计算速度很慢，现在不是了。你仍然可以保留你的分布假设，但至少要看看当你放松假设的时候会发生什么。做到这一点的方法是使用Bootstrap法，这个想法很直观和简单。
约翰-福克斯写道：”总体对样本来说，就像样本对引导程序样本一样”。但这是什么意思呢？你对来自样本的估计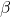
，应该是对 “真实”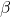，即总体的估计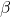，而这是未知的。现在从样本中抽取一个样本，我们称这个样本为Bootstrap样本，根据这个（Bootstrap）样本来估计你的情况，现在这个新的估计是对你原来的估计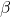，也就是来自原始数据的那个。为了清楚起见，假设你有3个观测值，第一个是{x=0.7,y=0.6}，第二个是{x=A,y=B}，第三个是{x=C,y=D}，现在，从样本中抽出的一个例子是洗牌排序：第一个是{x=A,y=B}，第二个是{x=0.7，y=0.6}，第三个是{什么什么}。这种 “洗牌 “就是我们所说的bootstrap样本，注意，任何观察值都可以被选择一次以上，或者根本不被选择，也就是说，我们是用替换法取样。现在我们再次估计同一统计量x=C,y=D}。这种 “洗牌 “就是我们所说的bootstrap样本，注意，任何观察值都可以被选择一次以上，或者根本不被选择，也就是说，我们是用替换法取样。现在我们再次估计同一统计量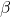（在我们的例子中）。
重复这个样本和估计很多次，你就有了许多Bootstrap估计，现在你可以检查表现。你可以用它来做一件事，就是为你的估计值自举Bootstrap置信区间（CI），而不需要基本的分布假设。
在 R
在 R 中，“boot”包可以解决问题：
library #加载软件包
# 现在我们需要我们想要估计的函数
# 在我们的例子中，是β。
bfun = function(da,b,fola){
# b是bootstrap样本的随机指数
return(lm$coef\[2\])
# 这是对β系数的解释
}
# 现在你可以进行自举了。
bt = boot
# R是多少个引导样本
plot
hist
您可以放大在每个bootstrap程序中选择了哪些索引，确切的排列是什么，可以使用函数 bay 来做到这一点：
zot = boot.array dim(zo) # 大小应该是R(bootstrap样本数)乘以n(你的数据的NROW) hist # 这是每一个指数的频率，对于第一个bootstrap运行，所以在这个直方图中，一个Y值比如说是3 #意味着在这个特定的bootstrap样本中，X值观察被选择了3次
随时关注您喜欢的主题
自己编写代码
如果您可以自己编写代码，就可以更好地理解它，对于像bootstrap置信区间这样的简单问题，它更加简单和快捷：
ptm <- pce() # 看一下它所花的时间
for (i in 1:nb){
uim = sample # 选择随机指数
bt\[i\] = lm
proc.time() - ptm # 在我这边大约80秒
您当前的置信区间怎么样？
真的有关系吗？也许这不值得麻烦。作为一个例子，我使用了已知有厚尾的股票收益，这意味着远离中心的更多观察样本。看看下图：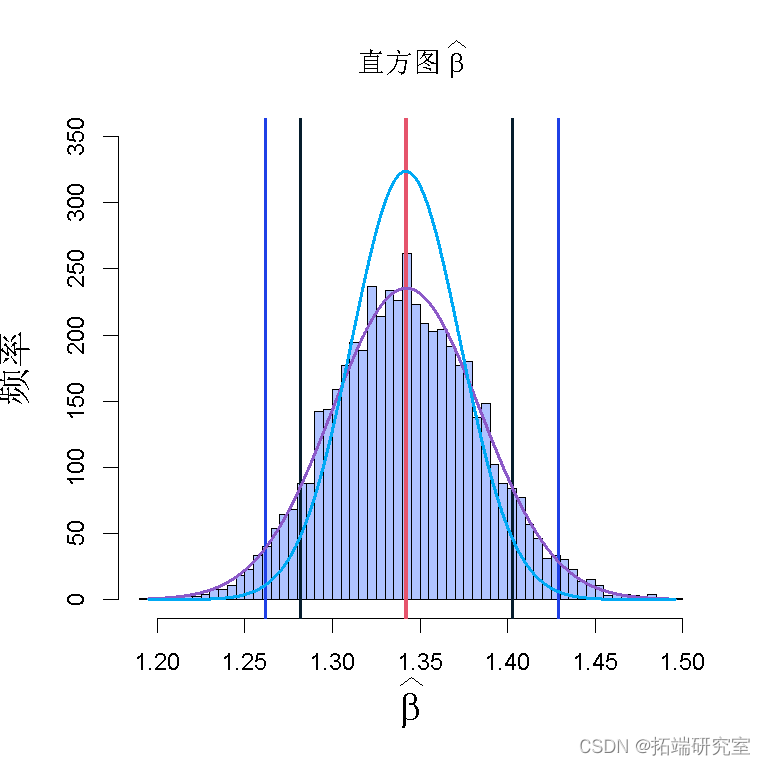
那就是摩根士丹利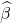 
与市场。估计值以 1.87 为中心。
黑色垂直线是“lm”函数报告的 (95%) 置信区间，蓝色垂直线是等效的非参数置信区间，浅蓝色曲线是正态密度。
注意到这个区间与非参数bootstrap法有多大区别，在这种情况下，非参数bootstrap 法更准确。例如，可能参数实际上是2，你可以看到软件的输出拒绝了这种可能性，因为它假定了正态性，然而引导法的置信区间确实涵盖了2这个值。
所以，一个投资者如果认为 “在我的投资组合中，所有的贝塔值都小于2，CI值为95%”，那么他就错误地认为摩根斯坦利是这样的。
这个检查需要大约80秒，所以我在把它插入双 “for “循环之前会三思而后行。然而，如果你是社会科学家，可以用这种稳健的分析来增强你的标准（正常）输出。
总结
在这里你可以看到，当你使用bootstrap的置信区间时，当正态分布假设有效时，_情况_并没有那么糟坏。我创建了一个假的正态分布，使用与报告相同的中心和标准差，并做了完全相同的分析。
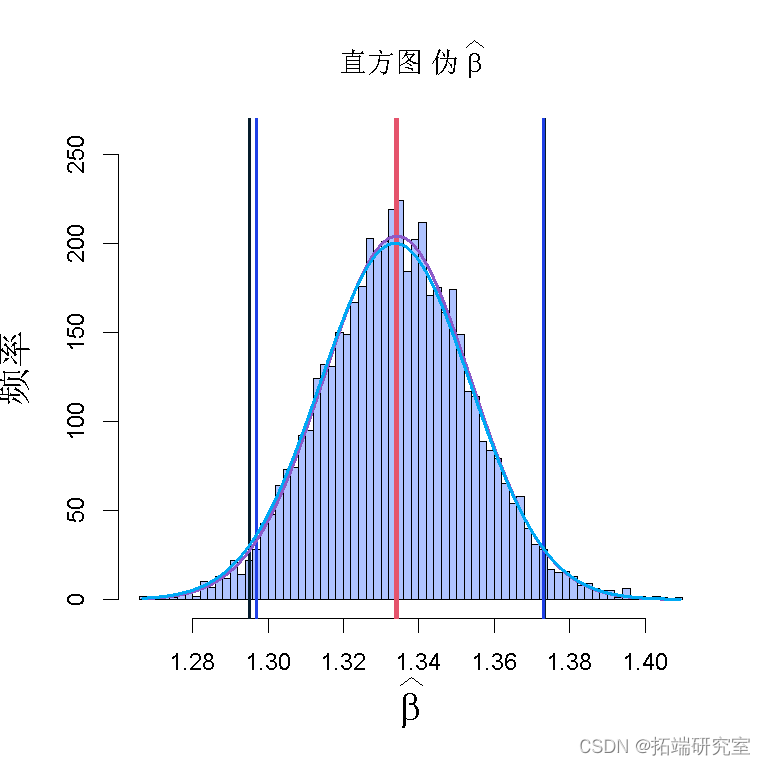
同样，我使用与 “lm “报告相同的中心和标准差从正态分布中进行了模拟，你可以看到区间是相互接近的，这就总结了这篇文章，使用参数化的置信区间，从假设的正态分布在某种意义上是次优的，因为即使是正态，你也不会损失很多。
谢谢阅读。
###################################################
### 现在我实际上是从正态分布中生成
###################################################
rnorm
lm2 = lm
for (i in 1:b){
uni = sample
fe\[i\] = lm
}
ftha <- boe
h2 = hist
xline
xfit<-seq
yfit<-dnorm
lines
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频】N-Gram、逻辑回归反欺诈模型文本分析招聘网站欺诈可视化|附数据代码
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
R语言分类回归分析考研热现象分析与考研意愿价值变现
R语言广义线性混合模型（GLMM）bootstrap预测置信区间可视化
