这里向您展示如何在R中使用glmnet包进行岭回归（使用L2正则化的线性回归），并使用模拟来演示其相对于普通最小二乘回归的优势。

由Kaizong Ye，Liao Bao撰写

当回归模型的参数被学习时，岭回归使用L2正则化来加权/惩罚残差。在线性回归的背景下，它可以与普通最小二乘法（OLS）进行比较。

可下载资源

岭回归

OLS定义了计算参数估计值（截距和斜率）的函数。它涉及最小化平方残差的总和。L2正则化是OLS函数的一个小增加，以特定的方式对残差进行加权以使参数更加稳定。结果通常是一种适合训练数据的模型，不如OLS更好，但由于它对数据中的极端变异（例如异常值）较不敏感，所以一般性更好。

岭回归：实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

思路：在原先的β的最小二乘估计中加一个小扰动λI，是原先无法求广义逆的情况变成可以求出其广义逆，使得问题稳定并得以求解。

称为关于岭参数λ的岭回归估计。

后面这一项

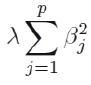
称为惩罚函数，它保证了β值不会变的很大。岭参数λ不同，岭回归系数也会不同。

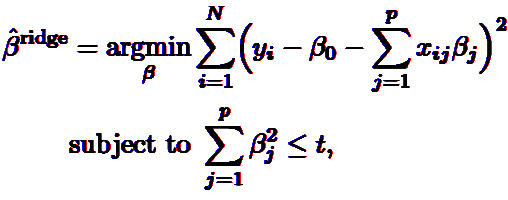
第二行是对第一行的一个约束项，也就是说所有系数β平方和应该<某个阈值t。

以两个变量为例，解释岭回归的几何意义:

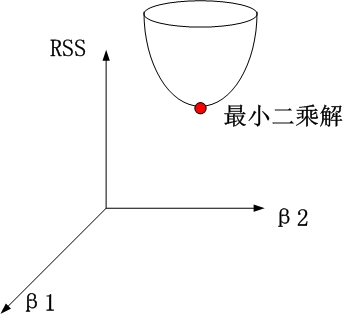
1、没有约束项时

系数β1和β2已经经过标准化。残差平方和RSS可以表示为β1和β2的一个二次函数，数学上可以用一个抛物面表示。

2、岭回归时

约束项为β12+β22≤t，对应着投影为β1和β2平面上的一个圆，即下图中的圆柱。

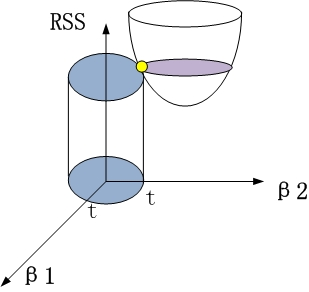
该圆柱与抛物面的交点对应的β1、β2值，即为满足约束项条件下的能取得的最小的β1和β2.

从β1β2平面理解，即为抛物面等高线在水平面的投影和圆的交点，如下图所示

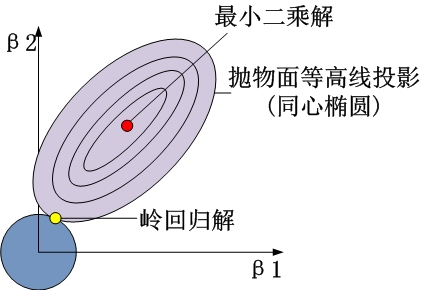
可见岭回归解与原先的最小二乘解是有一定距离的。

岭回归性质：

1）当岭参数为0，得到最小二乘解。

2）当岭参数λ趋向更大时，岭回归系数β估计趋向于0。

3）岭回归中的

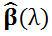
是回归参数β的有偏估计。它的结果是使得残差平和变大，但是会使系数检验变好，即R语言summary结果中变量后的*变多。

4）在认为岭参数λ是与y无关的常数时，是最小二乘估计的一个线性变换，也是y的线性函数。但在实际应用中，由于λ总是要通过数据确定，因此λ也依赖于y、因此从本质上说，并非的线性变换，也非y的线性函数。

5）对于回归系数向量来说，有偏估计回归系数向量长度<无偏估计回归系数向量长度，

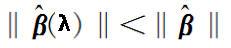
，即比理想值要短。

6）存在某一个λ，使得它所对应的的MSE（估计向量的均方误差）<最小二乘法对应估计向量的的MSE。

即存在λ>0，使得

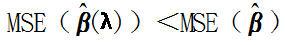
理解：和β平均值有偏差，但不能排除局部可以找到一个比更接近β。

岭迹图：

1）观察λ较佳取值；

2）观察变量是否有多重共线性；

可见，在λ很小时，通常各β系数取值较大；而如果λ=0，则跟普通意义的多元线性回归的最小二乘解完全一样；当λ略有增大，则各β系数取值迅速减小，即从不稳定趋于稳定。上图类似喇叭形状的岭迹图，一般都存在多重共线性。

λ的选择：一般通过观察，选取喇叭口附近的值，此时各β值已趋于稳定，但总的RSS又不是很大。

选择变量：删除那些β取值一直趋于0的变量。

注意：用岭迹图筛选变量并非十分靠谱。

参数的一般选择原则

选择λ值，使到

1）各回归系数癿岭估计基本稳定；

2）用最小二乘估计时符号不合理癿回归系数，其岭估计的符号变得合理；

3）回归系数没有不合乎实际意义癿值；

4）残差平方和增大不太多。一般λ越大，系数β会出现稳定的假象，但是残差平方和也会更大。

取λ的方法比较多，但是结果差异较大。这是岭回归的弱点之一。

岭回归选择变量的原则（不靠谱，仅供参考）

1）在岭回归中设计矩阵X已经中心化和标准化了，这样可以直接比较标准化岭回归系数癿大小。可以剔除掉标准化岭回归系数比较稳定且值很小癿自变量。

2）随着λ的增加，回归系数不稳定，震动趋于零的自变量也可以剔除。

3）如果依照上述去掉变量的原则，有若干个回归系数不稳定，究竟去掉几个，去掉哪几个，这幵无一般原则可循，这需根据去掉某个变量后重新进行岭回归分析的效果来确定。

包

我们将在这篇文章中使用以下软件包：

library(tidyverse)
library(broom)
library(glmnet)

与glmnet的岭回归

glmnet软件包提供了通过岭回归的功能glmnet()。重要的事情要知道：

它不需要接受公式和数据框架，而需要一个矢量输入和预测器矩阵。

您必须指定alpha = 0岭回归。

视频

Lasso回归、岭回归等正则化回归数学原理及R语言实例

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

岭回归涉及调整超参数lambda。glmnet()会为你生成默认值。另外，通常的做法是用lambda参数来定义你自己（我们将这样做）。

以下是使用mtcars数据集的示例：

因为，与OLS回归不同lm()，岭回归涉及调整超参数，lambda，glmnet()为不同的lambda值多次运行模型。我们可以自动找到最适合的lambda值，cv.glmnet()如下所示：

cv_fit <- cv.glmnet(x, y, alpha =0, lambda = lambdas)

cv.glmnet() 使用交叉验证来计算每个模型的概括性，我们可以将其视为：

plot(cv_fit)

交叉验证误差如下所示

曲线中的最低点指示最佳的lambda：最好使交叉验证中的误差最小化的lambda的对数值。我们可以将这个值提取为：

opt_lambda <- cv_fit$lambda.minopt_lambda#> [1] 3.162278

我们可以通过以下方式提取所有拟合的模型（如返回的对象glmnet()）：

这是我们需要预测新数据的两件事情。例如，预测值并计算我们训练的数据的R 2值：

y_predicted <- predict(fit, s = opt_lambda, newx = x)# Sum of Squares Total and Errorsst <- sum((y - mean(y))^2)sse <- sum((y_predicted - y)^2)# R squaredrsq <-1- sse / sstrsq#> [1] 0.9318896

最优模型已经在训练数据中占93％的方差。

Ridge v OLS模拟

通过产生比OLS更稳定的参数，岭回归应该不太容易过度拟合训练数据。因此，岭回归可能预测训练数据不如OLS好，但更好地推广到新数据。当训练数据的极端变化很大时尤其如此，当样本大小较低和/或特征的数量相对于观察次数较多时这趋向于发生。

下面是我创建的一个模拟实验，用于比较岭回归和OLS在训练和测试数据上的预测准确性。

我首先设置了运行模拟的功能：

最受欢迎的见解

1.R语言多元Logistic逻辑回归应用案例

2.面板平滑转移回归(PSTR)分析案例实现

3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）

4.R语言泊松Poisson回归模型分析案例

5.R语言回归中的Hosmer-Lemeshow拟合优度检验

6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标

现在针对不同数量的训练数据和特征的相对比例运行模拟（需要一些时间）：

d <- purrr::cross_d(list(n_train = seq(20,200,20),p_features = seq(.55,.95,.05)))d <- d %>%mutate(results = map2(n_train, p_features, repeated_comparisons))