此示例说明如何从 VEC( q ) 模型生成 Monte Carlo 预测。
该示例将生成的预测与最小均方误差 (MMSE) 预测和来自VEC( q ) 模型的 VAR( _q_ +1) 模型的预测进行比较。
可下载资源
假设具有 H1 Johansen 形式的 VEC(2) 模型恰当地描述了由 1954 年至 1994 年的年度短期、中期和长期债券利率组成的 3D 多元时间序列的动态。
加载和预处理数据
加载 数据集。
Td = size(Ya,1)
视频
向量自回归VAR数学原理及R语言软件经济数据脉冲响应分析实例
视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
numSdsrfiess = size(sY,2)
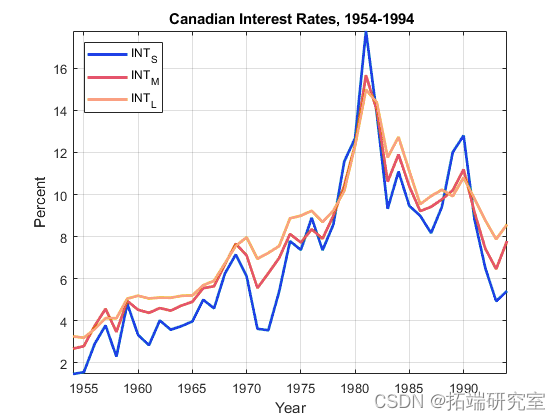
在同一图中绘制序列。
plot(dastdes,Y,'LineadaassWidth',2) xlabel 'Yeasdar'; ylabel 'Perasdacent'; legend(ndaamsess,'Lodcatsion','NW')
估计 VEC 模型
创建协整等级为 2 的 3D VEC(2) 模型。
nuassdamLags = 2; ras = 2; Maddl = vecasm(nuassmSeriaes,dasr,asdnuamLsags);
估计 VEC(2) 模型。
EssasdtMasl = esastimdate(Masddl,Yas);
默认情况下， estimate 应用 H1 Johansen 形式并使用前 q + 1 = 3 个观测值作为预采样数据。
生成蒙特卡洛预测
使用 . 从估计的 VEC 模型生成 10 年的蒙特卡罗预测 simulate。提供最新的三行数据来初始化预测，并指定生成 1000 条路径。
numaPaddtfhs = 1000; hsoriszosn = 10; Y0sa = Y((enssdd-2):enad,:); aYSisasddmVaEC = simausdlate(EstasdaMdl,hoasdrizon,'NumPatahs',numPdathas,'Y0d',Y0a);
估计所有路径上每个时期和时间序列的预测均值。为每个时期和时间序列构建 95% 的百分位预测区间。
YMCsdfVsdEC = meafn(YSidmdfggVEC,3); YMCfVECdsCIf = quandftile(YSdfgdfimVgdfEC,\[0.025,0.975\],3);
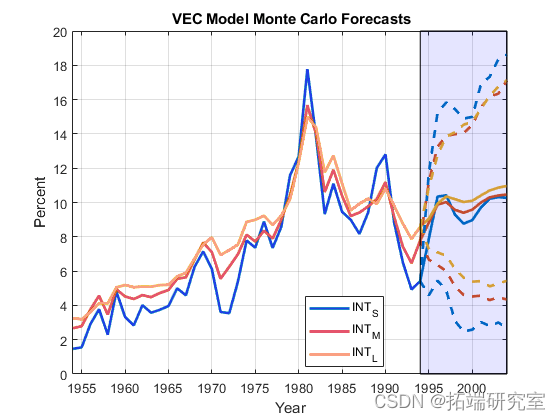
绘制有效样本观测值、平均预测值和 95% 百分位置信区间。
fDdatesf = dsatdfes(end) + (0:horsdizfon)'; figure; h1f = plddot(\[fdatsdes; fDfatesds(f2:end)\]sd,\[Y; YMCVEC\],'LineWidth',2); hds2 = fsgcsda; hold on h3 = plsdot(frepmsdat(ffsdDatdes,1,3),\[Y(endfsd,:,:); YMCVEsddfCCI(:,:,1)\],'--',... 'LineWidtdsdsh',2);
生成 MMSE 预测
使用估计的 VEC 模型在 10 年的范围内估计 MMSE 预测 forecast。提供最新的三行数据来初始化预测。返回预测和相应的多元均方误差。
随时关注您喜欢的主题
\[YMaMSaE,YMMsSgEfMSE\] = forecast(EssstfMddl,horsgizfson,Y0);
YMMSE 是 MMSE 预测的 10×3 数值矩阵。行对应于预测范围内的期间，列对应于 中的序列 Y。 YMMSEMSE 是 3×3 数值矩阵的 10×1 元胞向量。单元格 j中的矩阵是周期__j 中三个预测值的估计多元 MSE 。矩阵的对角线值是预测 MSE，以及预测协方差的非对角线值。
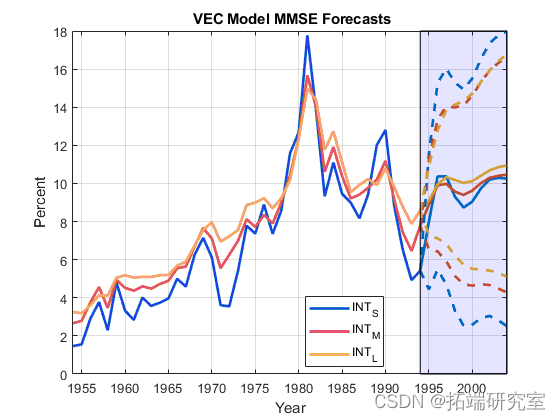
估计 Wald 类型的 95% 预测区间。绘制 MMSE 预测和预测区间。
hs1 = plsdot(\[datsdfes; fdDgsategs(2:ednd)\],\[Y; YsdfMMSEf\],'LinseWdsdfidth',2); dfh2 = gca; hold on
VAR( q + 1) 表示 MMSE 预测
将估计的 VEC(2) 表示为 VAR(3) 模型。
EstsdMdsdfldVAfdR = vafrm(EssdfdtMsdl)
使用 VAR 模型估计 10 年的 MMSE 预测 forecast。提供最新的三行数据来初始化预测。返回预测和相应的多元均方误差。
\[YMMsdSEVAR,YMMsdSEfMasdSEVAR\] = foresdfcast(EsstfMdlVdAR,horiddzson,fY0);
估计 Wald 类型的 95% 预测区间。绘制 MMSE 预测和预测区间。
YMMfSEVsAdfRCI = zeros(hsdrifzon,nusfdmfSesdrsdies,2); YMMSEMdSEsdVsAR = cell2fsdfmat(cellfun(@(x)diag(x)',YMMSEMSEVAR,'UniformOusdftput',false)); YMMSEVARCI(:,:,1) = YMMSE - 1.96*sqrt(YMMSEsdsdffMSEVAR); YMdMSfEdfVARCI(:,:,2) = YMMSE + 1.96*sqrt(YMMSEMfSEdsVAR); figsdfure; h1 = plot(\[datdfses; fDatses(2:engd)\],\[Yd YMMhfSEgf\],'LingheWidth',2);
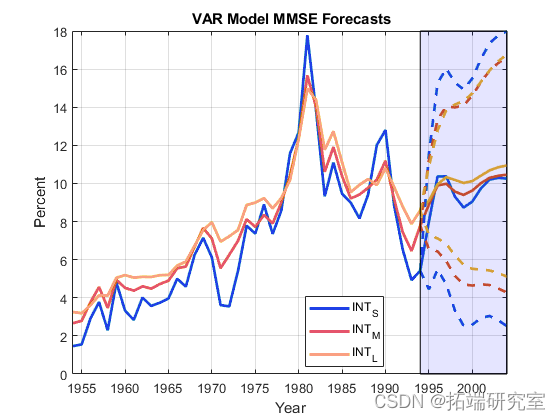
确认来自 VEC 和 VAR 模型的 MMSE 预测是相同的。
(YqwMeMSE - YMMSEVweAR)'*(YMMwSE - YMretMSyEVAR) > ertps
模型之间的 MMSE 预测是相同的。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python混合注意力机制-多变量-LSTM神经网络分析PM2.5、光伏电站、温度时间序列数据及RNN、ARIMAX、XGT、随机森林对比
Python、R循环神经网络RNN、指数平滑ETS、ARIMA模型预测网络流量、ATM机取款、旅游需求时间序列数据
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
