matlab软件在拟合数据时使用最小二乘法。

由Kaizong Ye，Coin Ge撰写

拟合需要一个参数模型，该模型将因变量数据与具有一个或多个系数的预测数据相关联。

拟合过程的结果是模型系数的估计。

可下载资源

为了获得系数估计，最小二乘法最小化残差的平方和。_第i_个数据点_ri_的残差定义为观测因变量值_yi_与拟合因变量值_ŷi_之间的差值，并标识为与数据相关的误差。

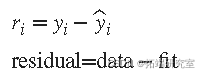
为了从一组离散数据 $（x_{i},y_{i}),i=0,1,2...m$ 中获得更多的信息，通常需要求出它的近似表达式。当数据是准确值时，可以用代数插值的方式求出原函数的近似表达式，但实际情况往往不是这样，我们观测或测试得到的数据往往都是含有误差的数据。针对这样的情况，最小二乘法就比较合适。

顾名思义，最小二乘法就是通过最小化误差项的平方来获得最优的估计值，因为误差的平方式一个关于优化变量的二次函数，具有非负性，必然存在最小值；但是，这个最小值不一定是唯一的，它可能是鞍点等局部最小值。

下面通过两个例子来帮助深入理解最小二乘法。

1.线性最小二乘-数据拟合

现有数据集 $D=\left\{ (x_{1},y_{1}),(x_{2},y_{2}),...(x_{m},y_{m})\right\}$ ,其中 $x_{i}$ 为输入数据， $y_{i}$ 为观测数据。为找到数据关系，对其进行如下式所示的n次多项式拟合(应该要先通过图像确定基函数，此处假设基函数为无常数项的n次多项式)。

$w_{1} x_{i}+w_{1} x_{i}^{2}+\ldots+w_{n} x_{i}^{n}=y_{i} ………………（1）$

由于误差的原因，拟合得到的 $y_{i}$ 是不准确的，我们记为 $y_{i}^{*}$ ，每一点产生的误差可以被描述为 $\delta_{i}=y_{i}^{*}-y_{i}$ ，进一步，整体的误差可表示为： $\delta=\sum_{i=1}^{m}{\delta_{i}}$ ，此式通常被称为误差方程。

要使近似表达式尽可能准确的反映数据的情况，只需令每一项的误差达到最小即可。此时问题转换为当参数 $w_{i}$ （待优化变量）取何值时，误差最小的问题。从误差方程的形式来看，直接求解比较困难，因此，考虑通过一些数学技巧来处理一下误差方程，使其更方便求解。

首先，如（2）式对误差进行平方，这样误差就可以保证非负，同时又是优化变量的二次函数，这样就可以用求极值的方式来寻找最小误差值，通常（2）式可以称为损失函数或误差函数。

$\frac{1}{2}\delta^2=\frac{1}{2}\sum_{i=1}^{m}{\delta_{i}^{2}}=\frac{1}{2}\left| \left| \delta\right|\right|_{2}…………（2）$

问题分析清楚，现在用矩阵的形式来进行求解，记 $Y=(y_1,y_2,\cdots,y_m)^T$ ,是 $m\times1$ 的列向量， $x$ 为 $m\times n$ 的输入矩阵：

$X=\left[\begin{array}{cccc} x_{1} & x_{1} ^{2}& \ldots & x_{1 } ^{n}\\ x_{2} & x_{2} ^{2}& \ldots & x_{2 }^{n} \\ \ldots & \ldots & \ldots & \ldots \\ x_{m} & x_{m}^{2} & \cdots & x_{m}^{n} \end{array}\right]$

待优化参数为 $w$ 是 $n\times 1$ 维列向量，记为 $w=\left[\begin{array}{l} w_{1} ,w_{2} ,\cdots w_{n}\end{array}\right]^{T}$ ，这方程组（1）可写为 $Xw=Y$ 。

此时，误差方程写为： $e(w)=\frac{1}{2}(Xw-y)^t(Xw-y)$

误差方程展开有：

$\begin{gathered} e(w)=\frac{1}{2}((X w-y)^{T}(X w-y))\\ = \frac{1}{2}(\left((X w)^{T}-y^{T}\right)(X w-y))\\ = \frac{1}{2}(w^{T} X^{T} X w-(X w)^{T} y-y^{T} X w+y^{T} y) \end{gathered}$

因为，任意两个列向量 $\alpha^{T} \beta=\beta^{T} \alpha$ ，上式可进一步简化：

$e(w)=\frac{1}{2}(w^{T} X^{T} X w-2(X w)^{T} y+y^{T} y)$

我们之前就已经明确，上式为待优化变量 $w$ 的函数，它的极值在 $w$ 导数为零处，所以我们对上式求 $w$ 的偏导：

$\frac{\partial e(w)}{\partial w}=2 X^{T} X w-2X ^{T} y$

令 $\frac{\partial e(w)}{\partial w}=0$ ，可得

$w=\left(X^{T} X\right)^{-1} X^{T} y$

此时的 $w$ 即为误差最小的多项式系数。

更一般的情况，基函数可以又多种形式，此时最小二乘问题的求解步骤为

（1）已知数据集后，确定输入矩阵（主要是基函数的确定），待优化变量

（2）列误差方程

（3）求误差方程关于待优化变量的偏导

（4）令导数为零，求解优化变量

2.非线性最小二乘法

在开始这个例子前首先要明确，什么是线性最小二乘和非线性最小二乘，此处所说的线性和非线性，是针对误差方程（注意，是误差方程不是误差函数）和待优化变量而言的，前面讨论的线性最小二乘问题中，误差方程是关于优化变量的一次函数，而非线性最小二乘即误差方程和优化变量不是一次关系或不满足线性条件（叠加性）。

下面对非线性最小二乘进行分析，和上面一样我们假定输入为 $X$ ，观测为 $Y$ ，待优化变量为 $w$ （注意此时的各个量和之前的不同，可以是多种形式，如矩阵等，不局限于向量），则非线性最小二乘问题可描述为：

$w=\arg \min _{w} \frac{1}{2}\|f(w)\|^{2}$

因为此时的误差 $f(w)$ 是非线性的，很难对其进行进一步的操作，因此，在求解之前，要对其进行线性化。对于非线性的问题，我们通常想到的是对其进行多项式近似，而泰勒公式正好为我们实现了这种设想。另外对于不方便直接求解的最小二乘问题，一般利用迭代的方式，即从一个初始值出发，给优化变量一个增量，不断的更新当前的优化变量，使目标函数下降（此处的迭代可以联系梯度下降对比理解）。

根据以上分析，我们利用泰勒公式，对误差进行一阶项线性近似，同时假设在 $f(w)$ 在 $w+\Delta w$ 处最小，则有

$min(f(w))=f(w+\Delta w)=f(w)+f^{\prime}(w) \Delta w=f(w)+J(w) \Delta w$

其中 $J(w)$ 是雅各比矩阵，为 $f(w)$ 对 $w$ 的偏导。

$J(w)=\left[\begin{array}{ccccc} \frac{\partial f_{1}}{\partial w_{1}} & \frac{\partial f_{1}}{\partial w_{2}} & \frac{\partial f_{1}}{\partial w_{3}} & \cdots & \frac{\partial f_{1}}{\partial w_{n}} \\ \frac{\partial f_{2}}{\partial w_{1}} & \frac{\partial f_{2}}{\partial w_{2}} & \frac{\partial f_{2}}{\partial w_{3}} & \cdots & \frac{\partial f_{2}}{\partial w_{n}} \\ \vdots & \vdots & \vdots & & \vdots \\ \frac{\partial f_{m}}{\partial w_{1}} & \frac{\partial f_{m}}{\partial w_{2}} & \frac{\partial f_{m}}{\partial w_{3}} & \cdots & \frac{\partial f_{m}}{\partial w_{n}} \end{array}\right]$ $,f_{1}...f_{m}为误差每一组数据的误差分量$

同样，在 $w+\Delta w$ 处此时误差函数也为零，即

$e(w)_{min}=\frac{1}{2}\|f(w+\Delta w)\|^{2} =\frac{1}{2}\left\{f(w)^{T} f(w)+2 f(w)^{T} J(w) \Delta w+\Delta w^{T} J(w)^{T} J(w) \Delta w\right\}$

也就是说,问题转化为求 $\Delta w$ 取何值时， $e(w)$ 达到最小的问题。这就好办了，我们将上式看为是关于 $\Delta w$ 的函数（即 $r(\Delta w)=e(w)_{min}$ ），这样只需确定函数极值点处的 $\Delta w$ 值，即为所求解。

因此，我们将上式对 $\Delta w$ 求偏导可得：

$\frac{\partial r(\Delta w)}{\partial \Delta w}=J(w)^{T} f(w) + J(w)^{T} J(w) \Delta w$

令导数为零，可得：

$J(w)^{T} J(w) \Delta w=-J(w)^{T} f(w)$

令 $H=J(w)^{T} J(w), \quad g=-J(w)^{T} f(w)$ ,有

$H \Delta x=g$

至此，在给定一个任意初值的条件下，求得此增量即可获得最优参数使得误差最小。

以上就是Gauss-Newton法求解非线性最小二乘问题的基本思路，可大概总结为：

（1）给定初始值 $w_{0}$

（2）对于第 $k$ 词迭代，求解当前的雅各比矩阵 $J(w_{k})$ 和误差 $f(w_{k})$

（3）求解增量方程： $H \Delta x=g$

（4）若 $\Delta w_{k}$ 足够小，则停止。否则，令 $x_{k+1}=x_{k}+\Delta x_{k}$

以上求解过程可以用Google的Ceres_Solver库进行求解。

以上为了推导的完整性，我们只讨论了增量的大小，没有考虑增量的方向，实际上，这个方向和值的大小同样重要。关于增量方向的问题，计划将在另一篇中分析。

残差的平方和由下式给出

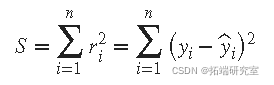
其中 n 是拟合中包含的数据点的数量， S 是误差估计的平方和。支持的最小二乘拟合类型包括：

线性最小二乘
加权线性最小二乘
稳健最小二乘
非线性最小二乘

自适应网页宽度的 Bilibili 视频

视频

线性混合效应模型(LMM,Linear Mixed Models)和R语言实现案例

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

误差分布

在拟合包含随机变化的数据时，通常会对误差做出两个重要假设：

误差仅存在于响应数据中，而不存在于预测数据中。
误差是随机的，并遵循均值为零且方差为 σ 2 的正态（高斯）分布。

第二个假设通常表示为

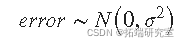
假设误差是正态分布的，因为正态分布通常为许多测量量的分布提供足够的近似值。

线性最小二乘

使用线性最小二乘法将线性模型拟合到数据。_线性_模型定义为系数为线性的方程。例如，多项式是线性的，但高斯不是。为了说明线性最小二乘拟合过程，假设您有 n 个可以通过一次多项式建模的数据点。

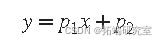
为了求解未知系数 p 1 和 p 2 的这个方程，你可以将 S 写成一个由两个未知数组成的 n 个 联立线性方程组。如果 n 大于未知数的数量。

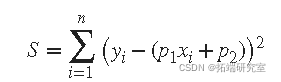
因为最小二乘拟合过程使残差的平方和最小化，所以通过对每个参数对_S_ 进行微分来确定系数，并将结果设置为零。

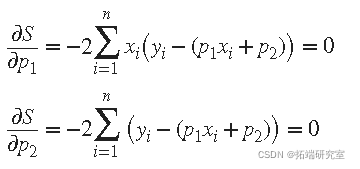
真实参数的估计值通常用 b_表示。_用b 1 和 b 2 代替 p 1_和 _p 2，前面的方程变为

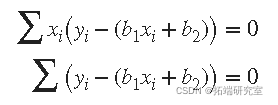
其中总和从 i = 1 到 n_。方程 定义为

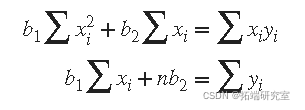
求解 b 1

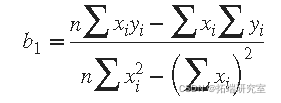
使用 b 1 值求解 b 2

最受欢迎的见解

1.R语言多元Logistic逻辑回归应用案例

2.面板平滑转移回归(PSTR)分析案例实现

3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）

4.R语言泊松Poisson回归模型分析案例

5.R语言回归中的Hosmer-Lemeshow拟合优度检验

6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标

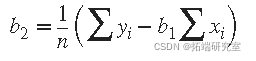
如您所见，估计系数 p 1 和 p 2 只需要一些简单的计算。将此示例扩展到更高次的多项式很简单，尽管有点乏味。所需要的只是添加到模型中的每个线性项的附加正规方程。

在矩阵形式中，线性模型由公式给出

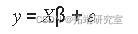
其中

y 是一个 n ×1 因变量向量。
β 是一个 m × 1 的系数向量。
X 是模型的 n × m 设计矩阵。
ε 是一个 n × 1 误差向量。

R语言中实现广义相加模型GAM和普通最小二乘(OLS)回归

阅读文章 ➜

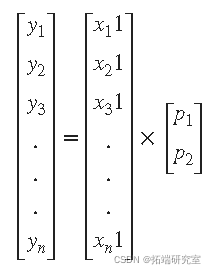
对于一次多项式，两个未知数中的 n 个 方程用 _y_、 _X_和 β 表示为

随时关注您喜欢的主题

该问题的最小二乘解是一个向量 _b_，它估计系数 β 的未知向量。正规方程由下式给出

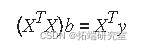
其中 XT 是设计矩阵 _X_的转置。求解 _b_，

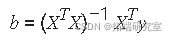
您可以将 _b_插回模型公式以获取预测的因变量值 _ŷ_。

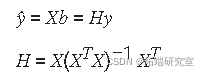
残差由下式给出

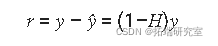
加权最小二乘

通常假设因变量数据具有恒定的方差。如果违反此假设，您的拟合可能会受到低质量数据的过度影响。为了改善拟合，您可以使用加权最小二乘回归，其中在拟合过程中包含一个额外的比例因子（权重）。加权最小二乘回归最小化误差估计

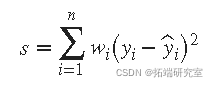
其中 wi 是权重。权重确定每个响应值对最终参数估计的影响程度。与低质量数据点相比，高质量数据点对拟合的影响更大。

如果权重已知，或者有理由证明它们遵循特定形式，则建议对数据进行加权。

您通常可以通过拟合数据和绘制残差来确定方差是否不恒定。在下面显示的图中，数据包含各种质量的重复数据，并且假设拟合是正确的。残差图中显示了质量差的数据，残差图具有“漏斗”形状，其中小的预测值在因变量值中产生的散布比大的预测值更大。

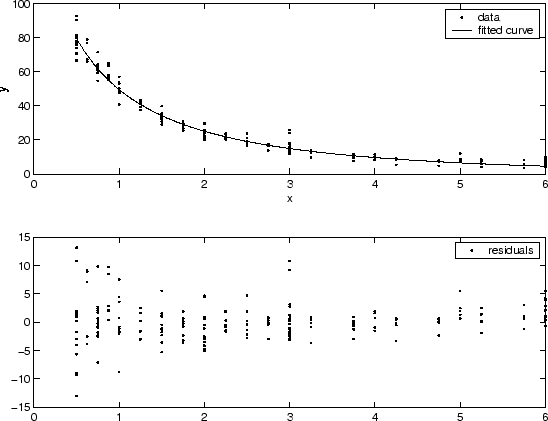
稳健最小二乘

通常假设因变量误差服从正态分布，极值很少见。_尽管如此，仍然会出现称为异常值_的极端值。

最小二乘拟合的主要缺点是它对异常值的敏感性。

异常值对拟合有很大影响，因为对残差进行平方会放大这些极端数据点的影响。为了最大限度地减少异常值的影响，您可以使用稳健的最小二乘回归拟合您的数据。

最小绝对残差 (LAR) — LAR 方法找到一条曲线，该曲线使残差的绝对差值（而不是平方差）最小化。因此，极值对拟合的影响较小。
Bisquare weights – 此方法最小化加权平方和，其中赋予每个数据点的权重取决于该点与拟合线的距离。线附近的点获得全部权重。离线较远的点会减轻重量。比随机机会预期的距离线更远的点的权重为零。在大多数情况下，双平方权重方法优于 LAR，因为它同时寻求使用通常的最小二乘法找到适合大部分数据的曲线，并且可以最大限度地减少异常值的影响。

双平方权重的稳健拟合使用迭代重新加权最小二乘算法，并遵循以下过程：

通过加权最小二乘拟合模型。
计算 调整后的残差 并将它们标准化。调整后的残差由下式给出

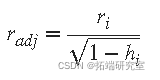
ri 是通常的最小二乘残差， hi 是通过减少高_杠杆_ 数据点的权重来调整残差的杠杆，这对最小二乘拟合有很大影响。标准化调整残差由下式给出

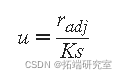
K 是等于 4.685 的调谐常数， s是由__MAD /0.6745 给出的稳健标准偏差，其中_MAD_ 是残差的中值绝对偏差。
计算鲁棒权重作为 _u_的函数。双方权重由下式给出
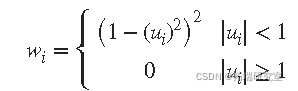
请注意，如果您提供自己的回归权重向量，则最终权重是稳健权重和回归权重的乘积。
如果拟合收敛，那么你就完成了。否则，通过返回第一步执行拟合过程的下一次迭代。

下图将常规线性拟合与使用双方权重的稳健拟合进行了比较。请注意，稳健拟合遵循大量数据，不受异常值的强烈影响。

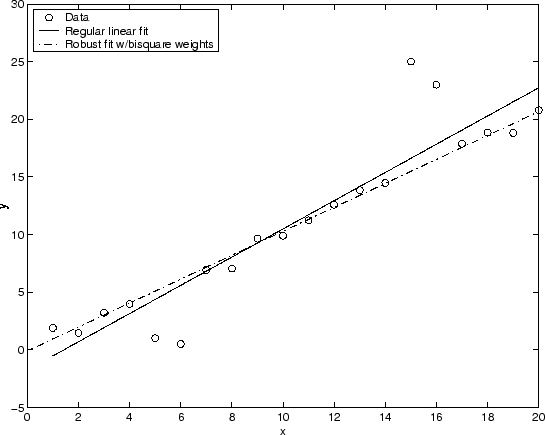
非线性最小二乘

使用非线性最小二乘公式将非线性模型拟合到数据。非线性模型定义为系数为非线性的方程，或系数为线性和非线性的组合。例如，高斯、多项式的比率和幂函数都是非线性的。

在矩阵形式中，非线性模型由公式给出

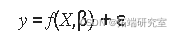
其中

y 是一个 n ×1 响应向量。
f 是 β 和 _X_的函数。
β 是一个 m × 1 的系数向量。
X 是模型的 n × m 设计矩阵。
ε 是一个 n × 1 误差向量。

非线性模型比线性模型更难拟合，因为无法使用简单的矩阵技术估计系数。相反，需要遵循以下步骤的迭代方法：

从每个系数的初始估计开始。对于一些非线性模型，提供了一种启发式方法，可以产生合理的起始值。对于其他模型，提供了区间 [0,1] 上的随机值。
生成当前系数集的拟合曲线。拟合因变量值 ŷ 由下式给出ŷ = f ( X , b )并且涉及计算 f ( X,b ) 的__雅可比行列式 ，它被定义为关于系数的偏导数矩阵。
调整系数并确定拟合是否有所改善。调整的方向和幅度取决于拟合算法。
通过返回到步骤 2 来迭代该过程，直到拟合达到指定的收敛标准。

您可以对非线性模型使用权重和稳健拟合，并相应地修改拟合过程。

稳健拟合示例

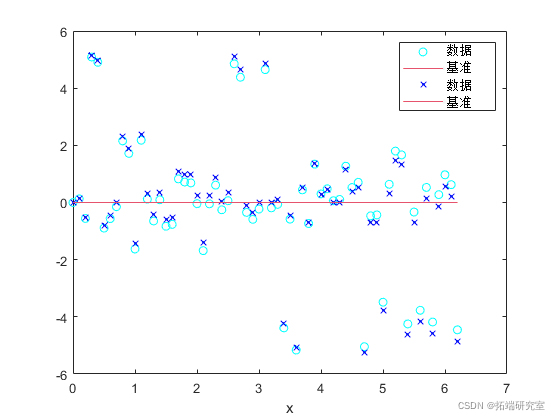
此示例显示如何比较排除异常值和稳健拟合的效果。该示例显示了如何从模型中排除大于 1.5 个标准差的任意距离处的异常值。然后，这些步骤将移除异常值与指定稳健拟合进行比较，从而降低异常值的权重。

创建基准正弦信号：

y0 = sin(xata);

向具有非恒定方差的信号添加噪声。

ydta = y0 + gnise + snise;

用基准正弦模型拟合噪声数据，并指定 3 个输出参数以获得包括残差在内的拟合信息。

f = ftye('a\*sin(b\*x)'); 
\[fi1,gof,fifo\] = fit(xdat

检查 fitinfo 结构中的信息。

从 fitinfo 结构中获取残差。

rsiduls = fno.rsis;

将“异常值”识别为距基准模型大于 1.5 标准差的任意距离处的点，并在排除异常值的情况下重新拟合数据。

I = abs( resls) > 1.5 * std( esda
outlrs = exclaa(xaa,dta,'ind

fit2 = fit(xdta,yda

将排除异常值的效果与在稳健拟合中给予它们较低的双方权重的效果进行比较。

绘制数据、异常值和拟合结果。指定一个信息图例。

plot(fit1,'r-',xda

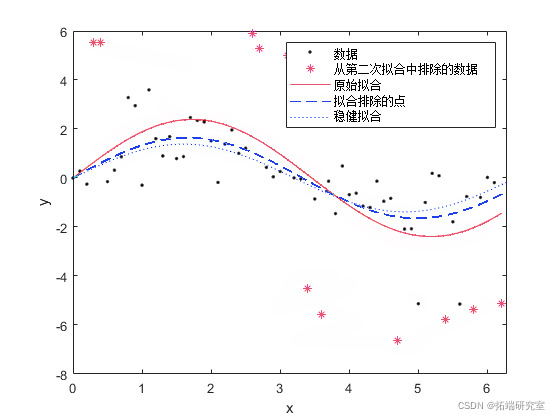
绘制考虑异常值的两个拟合的残差：

figure 
plot(fit2,xdata,ydat
hold on
plot(fit3,xdata,ydat
hold off

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

Matlab最小二乘法：线性最小二乘、加权线性最小二乘、稳健最小二乘、非线性最小二乘与剔除异常值效果比较

1.线性最小二乘-数据拟合

2.非线性最小二乘法

误差分布

线性最小二乘

R语言中实现广义相加模型GAM和普通最小二乘(OLS)回归

随时关注您喜欢的主题

加权最小二乘

如果权重已知，或者有理由证明它们遵循特定形式，则建议对数据进行加权。

稳健最小二乘

最小二乘拟合的主要缺点是它对异常值的敏感性。

非线性最小二乘

稳健拟合示例

相关文章

Matlab最小二乘法：线性最小二乘、加权线性最小二乘、稳健最小二乘、非线性最小二乘与剔除异常值效果比较

1.线性最小二乘-数据拟合

2.非线性最小二乘法

误差分布

线性最小二乘

R语言中实现广义相加模型GAM和普通最小二乘(OLS)回归

随时关注您喜欢的主题

加权最小二乘

如果权重已知，或者有理由证明它们遵循特定形式，则建议对数据进行加权。

稳健最小二乘

最小二乘拟合的主要缺点是它对异常值的敏感性。

非线性最小二乘

稳健拟合示例

相关文章

关注有关新文章的微信公众号