这篇文章探讨了为什么使用广义相加模型 是一个不错的选择。为此,我们首先需要看一下线性回归,看看为什么在某些情况下它可能不是最佳选择。
假设我们有一些带有两个属性Y和X的数据。如果它们是线性相关的,则它们可能看起来像这样:
a<-ggplot(my_data, aes(x=X,y=Y))+
geom_point()+ 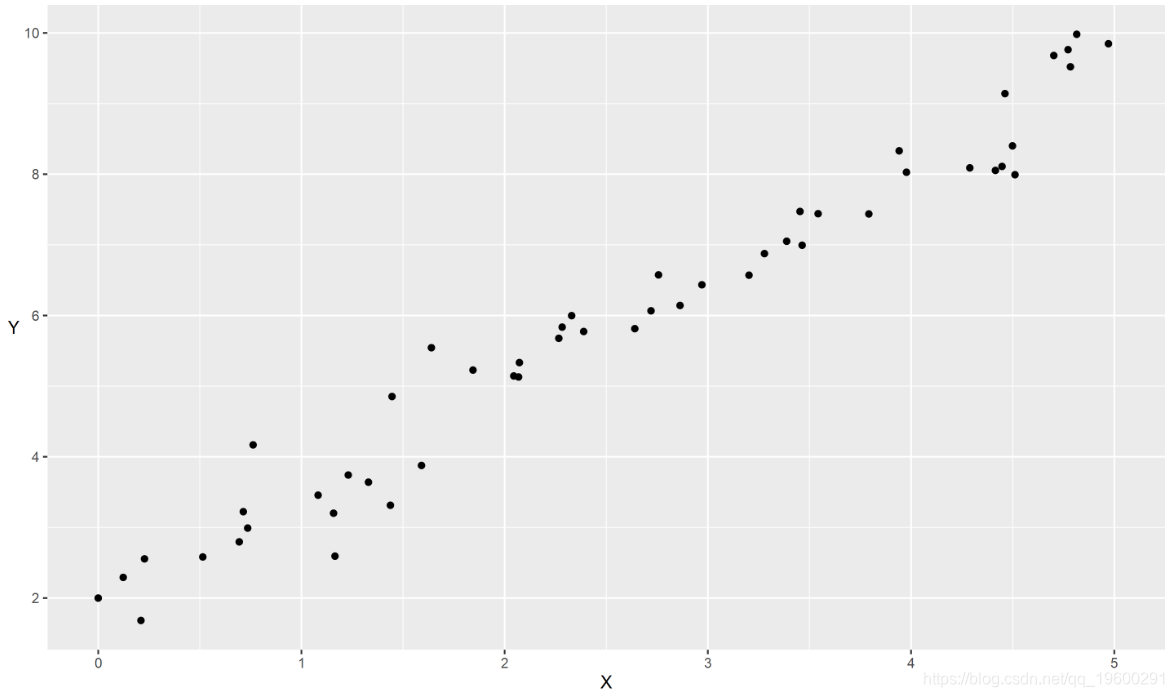
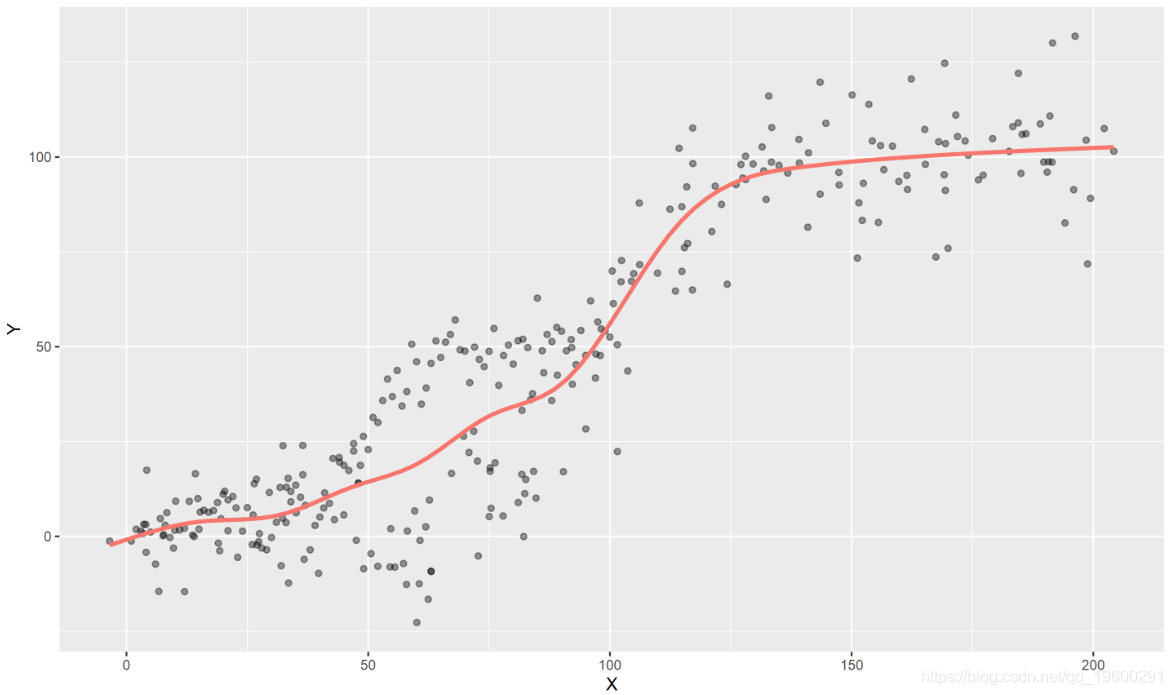
为了检查这种关系,我们可以使用回归模型。线性回归是一种使用X来预测变量Y的方法。将其应用于我们的数据将预测成红线的一组值:
a+geom_smooth(col="red", method="lm")+ 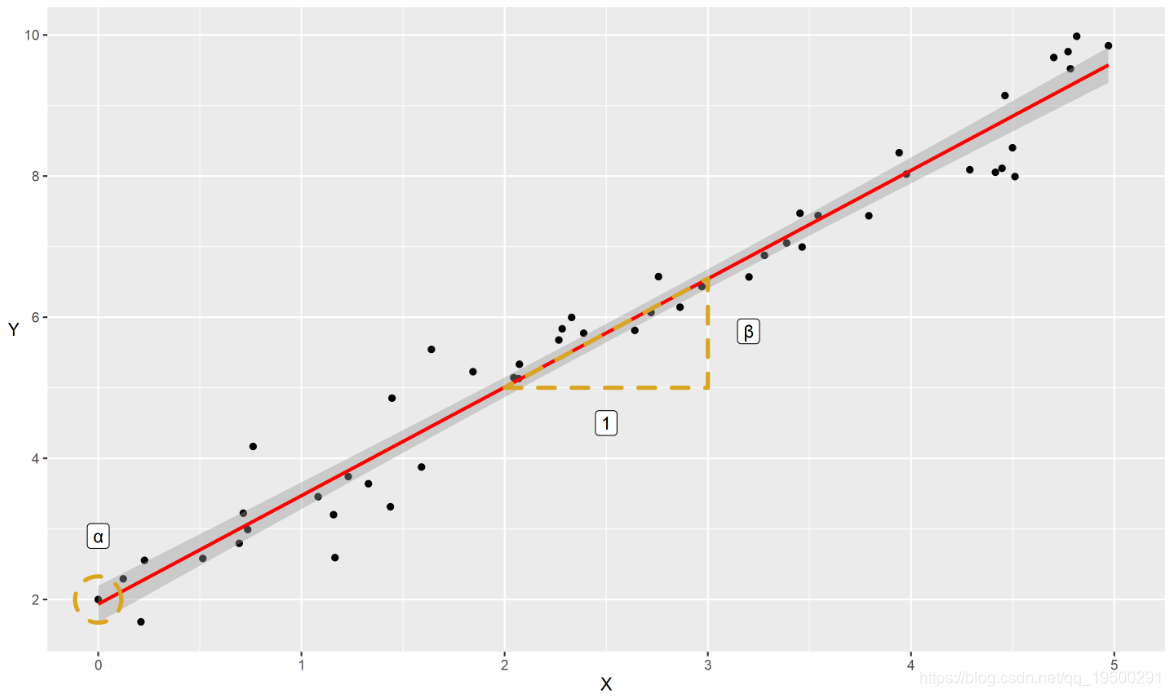
这就是“直线方程式”。根据此等式,我们可以从直线在y轴上开始的位置(“截距”或α)开始描述,并且每个单位的x都增加了多少y(“斜率”),我们将它称为x的系数,或称为β)。还有一点自然的波动,如果没有的话,所有的点都将是完美的。我们将此称为“残差”(ϵ)。数学上是:
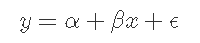
或者,如果我们用实际数字代替,则会得到以下结果:
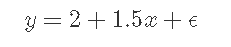
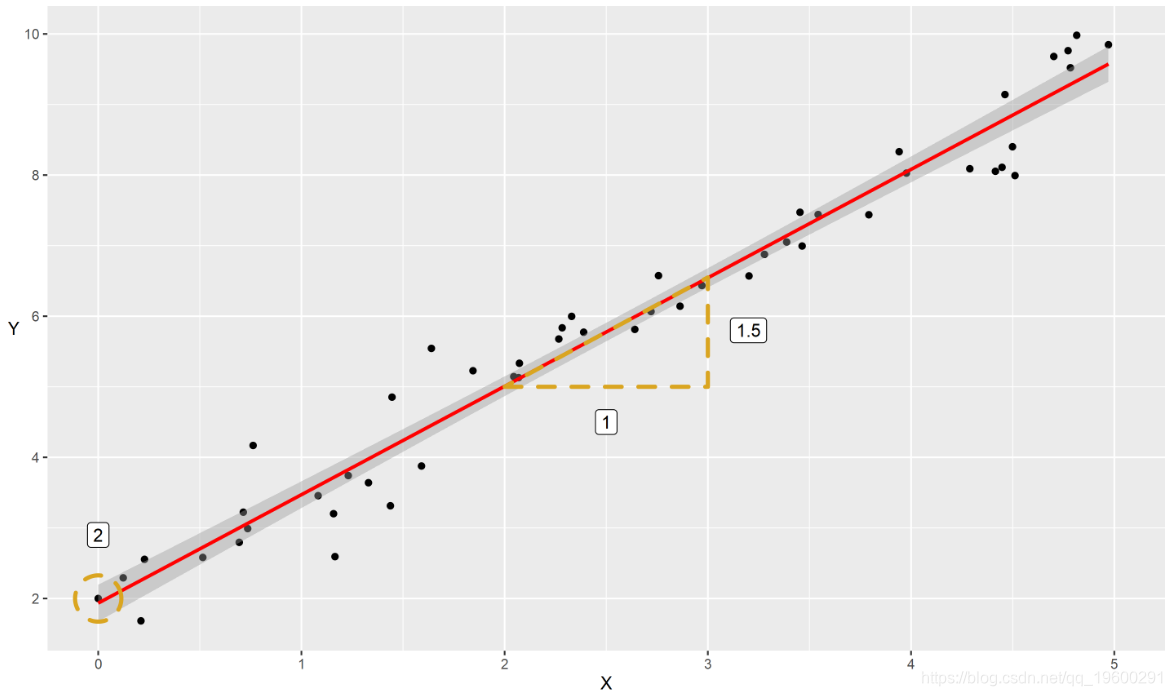
这篇文章通过考虑每个数据点和线之间的差异(“残差)然后最小化这种差异来估算模型。我们在线的上方和下方都有正误差和负误差,因此,通过对它们进行平方并最小化“平方和”,使它们对于估计都为正。这称为“普通最小二乘法”或OLS。
非线性关系如何?
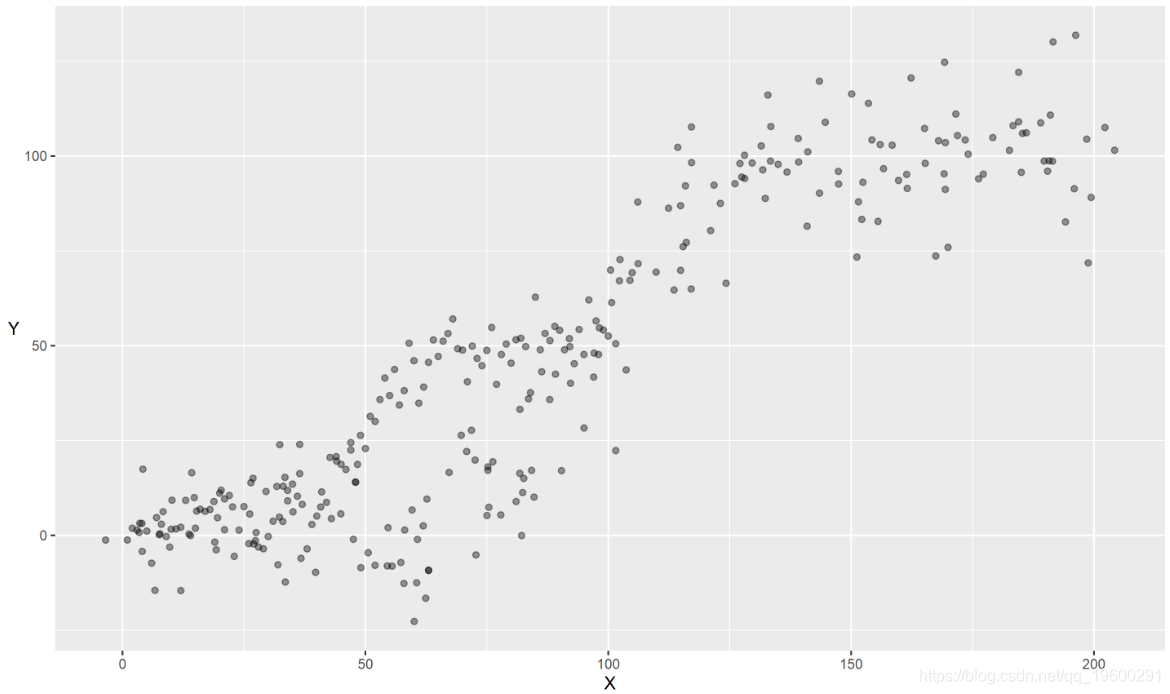
因此,如果我们的数据看起来像这样,我们该怎么办:
随时关注您喜欢的主题
我们刚刚看到的模型的关键假设之一是y和x线性相关。如果我们的y不是正态分布的,则使用广义线性模型 _(Nelder&Wedderburn,1972)_,其中y通过链接函数进行变换,但再次假设f(y)和x线性相关。如果不是这种情况,并且关系在x的范围内变化,则可能不是最合适的。我们在这里有一些选择:
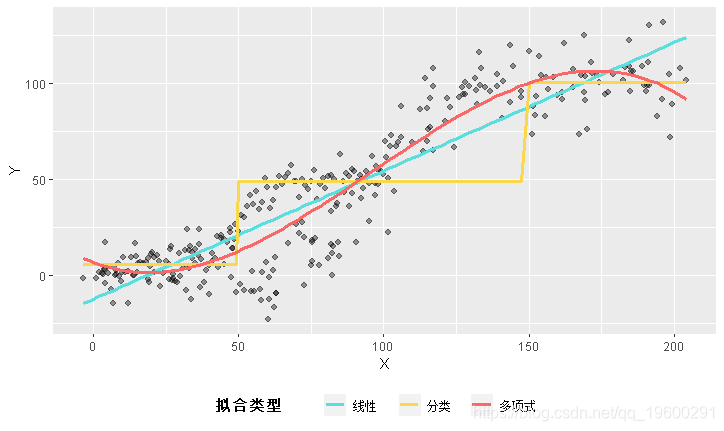
- 我们可以使用线性拟合,但是如果这样做的话,我们会在数据的某些部分上面或者下面。
- 我们可以分为几类。我在下面的图中使用了三个,这是一个合理的选择。同样,我们可能处于数据某些部分之下或之上,而在类别之间的边界附近似乎是准确的。例如,如果x = 49时,与x = 50相比,y是否有很大不同?
- 我们可以使用多项式之类的变换。下面,我使用三次多项式,因此模型适合:
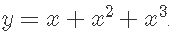
。这些的组合使函数可以光滑地近似变化。这是一个很好的选择,但可能会极端波动,并可能在数据中引起相关性,从而降低拟合度。
样条曲线
多项式的进一步细化是拟合“分段”多项式,我们在数据范围内将多项式链在一起以描述形状。“样条线”是分段多项式,以绘图员用来绘制曲线的工具命名。物理样条曲线是一种柔性条,可以弯曲成形,并由砝码固定。
在构造数学样条曲线时,我们有多项式函数(柔性条),二阶导数连续,固定在“结”点上。
下面是一个ggplot2 对象,该 对象的 geom_smooth 的公式包含ns 函数中的“自然三次样条” 。这种样条曲线为“三次”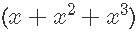
,并且使用10个结
光滑函数
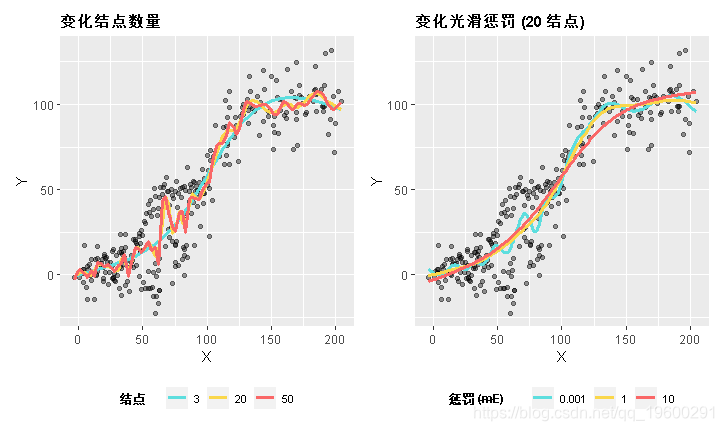
这可能会更接近数据,而且误差也会更小,但我们开始“过度拟合”关系,并拟合我们数据中的噪声。当我们结合光滑惩罚时,我们会惩罚模型中的复杂度,这有助于减少过度拟合。
样条曲线可以是光滑的或“摇摆的”,这可以通过改变节点数(k)或使用光滑惩罚γ来控制。如果我们增加结的数目,它将更“摇摆”。
广义相加模型(GAM)
广义加性模型(GAM)(Hastie,1984)使用光滑函数(如样条曲线)作为回归模型中的预测因子。这些模型是严格可加的,这意味着我们不能像正常回归那样使用交互项,但是我们可以通过重新参数化作为一个更光滑的模型来实现同样的效果。事实并非如此,但本质上,我们正转向一种模型,如:
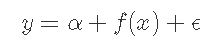
摘自Wood _(2017)_的GAM的更正式示例 是:
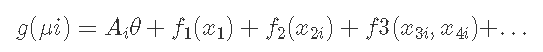
其中:
- μi≡E(Yi),Y的期望
- Yi〜EF(μi,ϕi),Yi是一个响应变量,根据均值μi和形状参数ϕ的指数族分布。
- Ai是任何严格参数化模型分量的模型矩阵的一行,其中θ为对应的参数向量。
- fi是协变量xk的光滑函数,其中k是每个函数的基础。
意义
如果您要建立回归模型,但怀疑光滑拟合会做得更好,那么GAM是一个不错的选择。它们适合于非线性或有噪声的数据。
gam拟合
那么,如何 为上述S型数据建立 GAM模型?在这里,我将使用三次样条回归 :
gam(Y ~ s(X, bs="cr")上面的设置意味着:
s()指定光滑器。还有其他选项,但是s是一个很好的默认选项bs=“cr”告诉它使用三次回归样条('basis')。- s函数计算出要使用的默认结数,但是您可以将其更改为k=10,例如10个结。
模型输出:
查看模型摘要:
##
## Family: gaussian
## Link function: identity
## Parametric coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 43.9659 0.8305 52.94 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Approximate significance of smooth terms:
## edf Ref.df F p-value
## s(X) 6.087 7.143 296.3 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## R-sq.(adj) = 0.876 Deviance explained = 87.9%
## GCV = 211.94 Scale est. = 206.93 n = 300- 显示了我们截距的模型系数,所有非光滑参数将在此处显示
- 每个光滑项的总体含义如下。
- 这是基于“有效自由度”(edf)的,因为我们使用的样条函数可以扩展为许多参数,但我们也在惩罚它们并减少它们的影响。
检查模型:
该 gam.check() 函数可用于查看残差图,但它也可以测试光滑器以查看是否有足够的结来描述数据。但是如果p值很低,则需要更多的结。
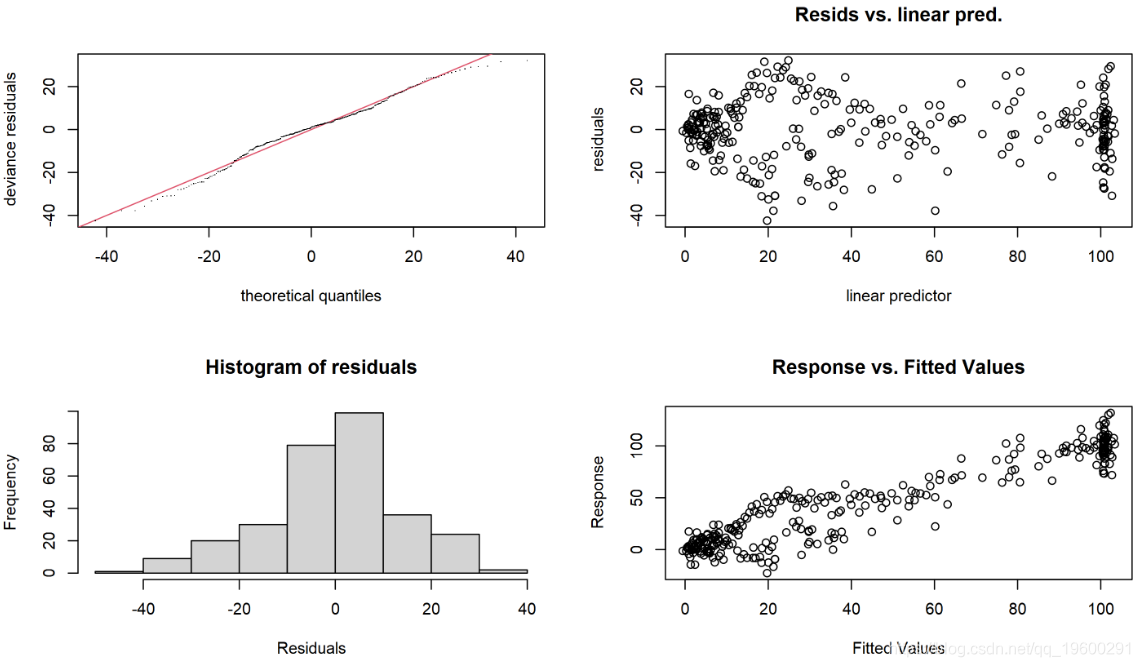
##
## Method: GCV Optimizer: magic
## Smoothing parameter selection converged after 4 iterations.
## The RMS GCV score gradient at convergence was 1.107369e-05 .
## The Hessian was positive definite.
## Model rank = 10 / 10
##
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
##
## k' edf k-index p-value
## s(X) 9.00 6.09 1.1 0.97它比线性模型好吗?
让我们对比具有相同数据的普通线性回归模型:
anova(my_lm, my_gam)## Analysis of Variance Table
##
## Model 1: Y ~ X
## Model 2: Y ~ s(X, bs = "cr")
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 298.00 88154
## 2 292.91 60613 5.0873 27540 26.161 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1我们的方差分析函数在这里执行了f检验,我们的GAM模型明显优于线性回归。
小结
所以,我们看了什么是回归模型,我们是如何解释一个变量y和另一个变量x的。其中一个基本假设是线性关系,但情况并非总是这样。当关系在x的范围内变化时,我们可以使用函数来改变这个形状。一个很好的方法是在“结”点处将光滑曲线链接在一起,我们称之为“样条曲线”
我们可以在常规回归中使用这些样条曲线,但是如果我们在GAM的背景中使用它们,我们同时估计了回归模型以及如何使我们的模型更光滑。
上面的示例显示了基于样条的GAM,其拟合度比线性回归模型好得多。
参考
- NELDER, J. A. & WEDDERBURN, R. W. M. 1972. Generalized Linear Models. Journal of the Royal Statistical Society. Series A (General), 135, 370-384.
- HARRELL, F. E., JR. 2001. Regression Modeling Strategies, New York, Springer-Verlag New York.


 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 Python、R语言南方电网、电力负荷数据多模型构建:分位数回归、GAM样条曲线、指数平滑和SARIMA与预测实践
Python、R语言南方电网、电力负荷数据多模型构建:分位数回归、GAM样条曲线、指数平滑和SARIMA与预测实践 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据 R基于贝叶斯加法回归树BART、MCMC的DLNM分布滞后非线性模型分析母婴PM2.5暴露与出生体重数据及GAM模型对比、关键窗口识别
R基于贝叶斯加法回归树BART、MCMC的DLNM分布滞后非线性模型分析母婴PM2.5暴露与出生体重数据及GAM模型对比、关键窗口识别



