
此示例探讨了如何使用多因素copula模型模拟相关的交易违约。
鉴于违约风险敞口,违约概率和违约信息损失,估计交易对手组合的潜在损失。一个creditDefaultCopula对象用于每个债务人的信用与潜在变量模型。
可下载资源
潜在变量由一系列加权潜在信用因子以及每个债务人的特殊信用因子组成。潜在变量根据其默认概率映射到每个方案的债务人的默认或非默认状态。该creditDefaultCopula对象支持投资组合风险度量,交易对手级别的风险贡献以及模拟收敛信息。
这个例子还探讨了风险度量对用于模拟的copula(高斯copula与t copula)类型的敏感性。
加载和检查投资组合数据
在此,简单介绍copula的基本知识,以二元copula为例。
定义1.1 :若二元函数 C(u,v) 满足
1) C的定义域: U=(u,v)∈[0,1]2 ;
2) C(u,v) 有零基面且是二维递增的;
3) 对于U中的任意两点 u,v ,有 C(u,0)=0=C(0,v),C(u,1)=u,C(1,v)=v
4) 对于U中的任意四个点 u1,u2,v1,v2 ,如果 u1≤u2,v1≤v2 ,则
C(u2,u2)−C(u2,v1)−C(u1,v2)=C(u1,v1)≥0
则称函数 C(u,v) 为Copula函数。
定理1.1:(Sklar定理)设二维随机变量 (X1,X2) 的联合分布为 F(x1,x2) ,边缘分布分别为 F1(x1) 、 F2(x2) ,则对 ∀(x1,x2)∈R2 ,存在一个Copula函数C,使得
F(x1,x2)=C(F1(x1),F(x2)) (1)
若 F1(x1) 、 F2(x2) 都是连续的,那么C是唯一存在的;反之,若 F1(x1) 、 F2(x2) 是一元分布函数, C(u1,u2) 为对应的Copula函数,那么(1)式定义的 F(x1,x2) 函数是一个多元联合分布函数,边缘分布为 F1(x1) 、 F2(x2) 。这个定理描述了Copula函数和边缘分布函数的关系,指出可以通过一个Copula连接函数将一个多维联合概率分布函数同其对应的一维边缘概率分布函数结合起来。
Aas和Czado (2009) 在文章中详细介绍了Pair-Copula的相关理论,认为多元变量联合密度函数按照某种结构可分解为一系列Pair-Copula密度函数和边缘分布函数的乘积。对于n维随机变量向量 X=(x1,x2,⋯,xn) ,根据条件密度函数性质,X的联合密度函数可表示为
f(x1,x2,⋯,xn)=fn(xn)⋅f(xn−1|xn)⋅f(xn−2|xn−1,xn)⋅⋯⋅f(x1|x2,⋯,xn) (2)
根据定理1.1,多元变量联合分布函数的密度函数可表示为
f(x1,x2,⋯,xn)=c12⋯n(F1(x1),F2(x2),⋯,Fn(xn))⋅f1(x1)⋅⋯⋅fn(xn) (3)
其中, c12⋯n 为n维Copula密度函数, fi(xi) 为边缘密度函数。
进而推导可得,任一条件密度函数可分解为二元Copula与条件密度函数,表达式为:
f(x|v)=cxvj|v−j(F(x|v−j),F(vj|v−j))⋅f(x|v−j) (4)
其中, vj 为n维向量v中的任一分量, v−j 为v除去 vj 的 n−1 维分量, F(x|v) 为条件边际分布函数。对于任意的j, cxvj|v−j(⋅|⋅) 是二元Pair-Copula密度函数,有
f(x|v)=∂Cxvj∣∣v−j(F(x|v−j),F(vj|v−j))∂F(vj|v−j) (5)
投资组合包含100个交易对手及其相关的信用风险敞口(默认值EAD),违约概率(PD)和默认损失(LGD)。使用creditDefaultCopula对象,您可以模拟某个固定时间段(例如,一年)的默认值和损失。的EAD,PD和LGD输入必须是针对特定的时间范围。
在此示例中,每个交易对手都使用一组权重映射到两个基础信用因子。该Weights2F变量是一个NumCounterparties-by-3矩阵,其中每一行包含一个单一的对方的权重。前两列是两个信用因子的权重,最后一列是每个交易对手的特殊权重。此示例(FactorCorr2F)中还提供了两个基本因子的相关矩阵。
加载CreditPortfolioData.mat
使用creditDefaultCopula投资组合信息和因子相关性初始化对象。
rng('default');
cc = creditDefaultCopula(EAD,PD,LGD,Weights2F,'FactorCorrelation',FactorCorr2F);
cc.VaRLevel = 0.99;
DISP(CC)
creditDefaultCopula with properties:
FactorCorrelation:[2x2 double]
VaRLevel:0.9900
PortfolioLosses:[]
cc.Portfolio(1:5,:)
ans =
5x5表
ID EAD PD LGD重量
__ ______ _________ ____ ____________________
1 21.627 0.0050092 0.35 0.35 0 0.65
2 3.2595 0.060185 0.35 0 0.45 0.55
3 20.391 0.11015 0.55 0.15 0 0.85
4 3.7534 0.0020125 0.35 0.25 0 0.75
5 5.7193 0.060185 0.35 0.35 0 0.65模拟模型和绘制潜在损失
使用该simulate函数模拟多因素模型。默认情况下,使用高斯copula。此函数在内部将已实现的潜在变量映射到默认状态,并计算相应的损失。在模拟之后,creditDefaultCopula对象使用模拟结果填充PortfolioLosses和CounterpartyLosses属性。
cc = simulate(cc,1e5);
DISP(CC)
creditDefaultCopula with properties:
FactorCorrelation:[2x2 double]
VaRLevel:0.9900
PortfolioLosses:[1x100000双]该portfolioRisk函数返回总投资组合损失分布的风险度量,并且可选地返回它们各自的置信区间。VaRLevel在creditDefaultCopula对象的属性中设置的级别报告风险值(VaR)和条件风险值(CVaR)。
[pr,pr_ci] = portfolioRisk(cc);
fprintf('投资组合风险指标:\ n');
DISP(PR)
fprintf('\ n \ n风险衡量的保密间隔:\ n');
DISP(pr_ci)
投资组合风险衡量
EL Std VaR CVaR
______ ______ ______ ______
24.774 23.693 101.57 120.22
风险衡量的置信区间:
EL Std VaR CVaR
________________ ________________ ________________ _______________
24.627 24.92 23.589 23.797 100.65 102.82 119.1 121.35看看投资组合损失的分布。预期损耗(EL),VaR和CVaR标记为垂直线。由VaR和EL之间的差异给出的经济资本显示为EL和VaR之间的阴影区域。
plotline = @(x,color)plot([xx],ylim,'LineWidth',2,'Color',color);
cvarline = plotline(pr.CVaR,'m');
%遮蔽预期损失和经济资本的领域。
plotband = @(x,color)patch([x fliplr(x)],[0 0 repmat(max(ylim),1,2)],...
color,'FaceAlpha',0.15);
elband = plotband([0 pr.EL],'blue');
ulband = plotband([pr.EL pr.VaR],'red');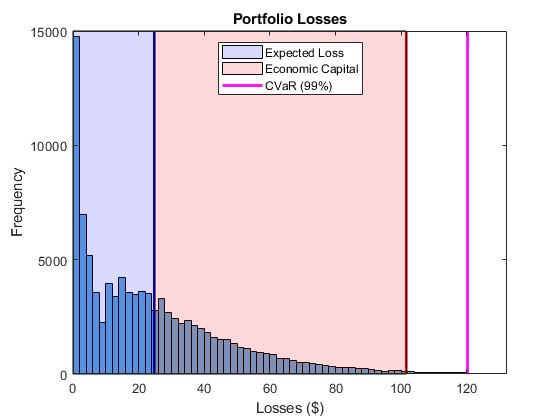
找出交易对手的集中风险
使用该riskContribution函数查找投资组合中的集中度风险。riskContribution返回每个交易对手对投资组合EL和CVaR的贡献。这些附加值贡献与相应的总投资组合风险度量相加。
rc = riskContribution(cc);
报告EL和CVaR的风险贡献百分比。
RC(1:5,:)
ans =
5x5表
ID EL Std VaR CVaR
__ _________ __________ _______ _________
1 0.038604 0.02495 0.10482 0.12868
2 0.067068 0.036472 0.17378 0.24527
3 1.2527 0.62684 2.0384 2.3103
4 0.0023253 0.00073407 0 0.0026274
5 0.11766 0.042185 0.27028 0.26223通过CVaR贡献找出风险最大的交易对手。
[rc_sorted,idx] = sortrows(rc,'CVaR','descend');
rc_sorted(1:5,:)
ans =
5x5表
ID EL Std VaR CVaR
__ _______ ______ ______ ______
89 2.261 2.2158 8.1095 9.2257
22 1.5672 1.8293 6.275 7.4602
66 0.85227 1.4063 6.3827 7.2691
16 1.6236 1.5011 5.8949 7.1083绘制交易对手风险和CVaR贡献。具有最高CVaR贡献的交易对手以红色和橙色绘制。
pointSize = 50;
colorVector = rc_sorted.CVaR;
scatter(cc.Portfolio(idx,:)。EAD,rc_sorted.CVaR,...
pointSize,colorVector,'filled')
colormap('jet')
用置信带研究模拟收敛性
使用该confidenceBands函数来研究模拟的收敛性。
默认情况下,会报告CVaR置信区间,但使用可选RiskMeasure参数支持所有风险度量的置信区间。
cb = confidenceBands(cc);
%置信带存储在表格中。
CB(1:5,:)
ans =
5x4表
NumScenarios降低CVaR上限
____________ ______ ______ ______
1000 113.92 124.76 135.59
2000 111.02 117.74 124.45
3000 113.58 118.97 124.36
4000 113.06 117.44 121.81
5000 114.38 118.99 123.6绘制置信区间以查看估算收敛的速度。
随时关注您喜欢的主题
找到必要数量的方案以获得特定宽度的置信区间。
width =(cb.Upper - cb.Lower)./ cb.CVaR;
plot(cb.NumScenarios,width * 100,'LineWidth',2);
%找到置信带在
%CVaR的1%(双侧)范围内的点。
thresh = 0.02;
scenIdx = find(width <= thresh,1,'first');
scenValue = cb.NumScenarios(scenIdx);
widthValue = width(scenIdx);
比较Gaussian和t Copulas的尾部风险
切换到t copula会增加交易对手之间的默认关联。这导致投资组合损失的尾部分布更加严重,并且在压力情景中导致更高的潜在损失。
cc_t = simulate(cc,1e5,'Copula','t');
pr_t = portfolioRisk(cc_t);
了解投资组合风险如何随着t copula而变化。
高斯copula的投资组合风险:
EL Std VaR CVaR
______ ______ ______ ______
24.774 23.693 101.57 120.22
t copula的投资组合风险(dof = 5):
EL Std VaR CVaR
______ ______ ______ ______
24.924 38.982 186.33 251.38比较每种型号的尾部损失。
使用具有五个自由度的t copula,尾部风险测量值VaR和CVaR显着更高。t copulas 的默认相关性较高,因此有多个交易对手默认的情况更多。自由度的数量起着重要作用。对于非常高的自由度,使用t copula的结果与使用高斯copula的结果相似。五是自由度非常低,因此结果显示出显着的差异。此外,这些结果强调极端损失的可能性对于copula的选择和自由度的数量非常敏感。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python+AI提示词用贝叶斯方法Copula进行参数推断可视化|附数据代码
Python+AI提示词用贝叶斯方法Copula进行参数推断可视化|附数据代码 MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究
MATLAB用CNN-LSTM神经网络的语音情感分类深度学习研究 R语言VAR模型的多行业关联与溢出效应可视化分析
R语言VAR模型的多行业关联与溢出效应可视化分析 马尔可夫转换MSVAR模型预测资产收益率时间序列可视化分析|附数据代码
马尔可夫转换MSVAR模型预测资产收益率时间序列可视化分析|附数据代码
