使用冗余预测变量构建数据集并使用lasso 和glm识别这些预测变量 。
使用lasso正则化去除冗余预测变量
创建一个X 包含 100 个观测值和 10 个预测变量的随机矩阵 。y 仅使用四个预测变量和少量噪声创建正态分布因变量 。
默认值 randn ; X*权重 + randn*0.1; % 小的附加噪音
可下载资源
执行lasso正则化。
lasso
求第 75 个Lambda 值 的系数向量 B。

1. lasso回归与岭回归的异同
如下,如果已知模型中的很多变量为无关变量,如astrological offset和airspeed scalar等,我们倾向于选择lasso回归,从而使得拟合模型更加简洁和便于解读。
Size = y-intercept + slope x Weight + diet differece x Hight Fat Diet +
+ astrological offset x Sign + airspeed scalar x Airspeed of Swallow
如下,如果模型中有非常多的变量,我们无法知道其是否是无关变量,如基于10000个基因的表达预测小鼠体积。在这种情况下,我们应该选择lasso回归,还是岭回归呢?
答案是弹性网络回归(Elastic Net Regression)。听名字非常炫酷,有弹性的回归,意味着它非常灵活能适应多用场景。简单来说,弹性网络回归是lasso回归和岭回归的结合版本。
2. 弹性网络回归是lasso回归和岭回归的结合版
公式解读:弹性网络回归包含lasso回归和岭回归非惩罚项,两种惩罚项的λ系数不同(lasso回归λ1,岭回归λ2)。基于使用多个不同λ1和λ2的交叉验证,以寻找最佳λ1和λ2的取值。
当λ1 = 0,λ2 = 0时,弹性网络回归与最初的最小二乘法线性回归拟合的模型一致。
当λ1 = 0,λ2 > 0时,弹性网络回归与lasso回归拟合的模型一致。
当λ1>0,λ2 = 0时,弹性网络回归与岭回归拟合的模型一致。
当λ1>0,λ2>0时,弹性网络回归为岭回归和lasso回归的结合版本。
识别并删除冗余预测变量。
广义线性模型的交叉验证lasso正则化
从泊松模型构建数据,并使用 确定重要的预测变量 lassoglm。
创建具有 20 个预测变量的数据。仅使用三个预测变量加上一个常数来创建泊松因变量。
rng % 用于重现性 randn exp(X)*weights + 1
构建数据的泊松回归模型的交叉验证lasso正则化。
检查交叉验证图以查看Lambda 正则化参数的效果 。
Plot('CV');
legend
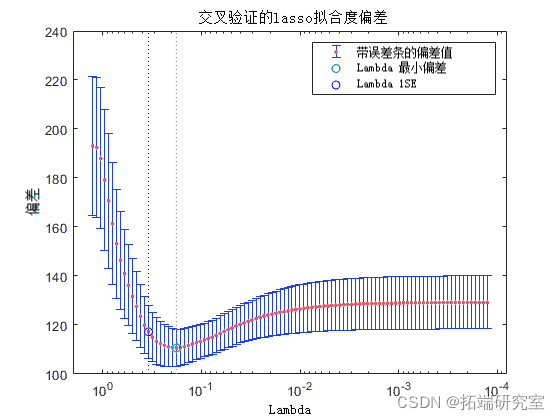
绿色圆圈和虚线定位 Lambda 交叉验证误差最小的位置。蓝色圆圈和虚线定位具有最小交叉验证误差加一个标准偏差的点。
找到对应于两个识别点的非零模型系数。
FitInf find(B

FitInf min1fnd(B)
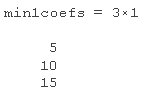
来自最小加一标准误差点的系数正是用于创建数据的那些系数。
使用lasso正则化预测值
加载 考试成绩 数据集。将上次考试成绩转换为逻辑向量,其中 1 代表80以上的成绩, 0代表80以下的成绩。
ynm = (y>=80);
将数据划分为训练集和测试集。
rng default % 设置可重复性的种子 Xi = X(iTain,:); yran = yBinom yTe = yBinom
对训练数据进行 3 折交叉验证,对广义线性模型回归执行lasso正则化。假设 中的值 y 是二项分布的。选择对应于Lambda 最小预期偏差的模型系数 。
lasso(Trn,Tain,'binomial','CV',3); ince = FitIiance; FitIept
随时关注您喜欢的主题

使用在上一步中找到的模型系数预测测试数据的考试成绩。使用 指定二项式因变量的链接函数 'logit'。将预测值转换为逻辑向量。
使用混淆矩阵确定预测的准确性。
confuhart
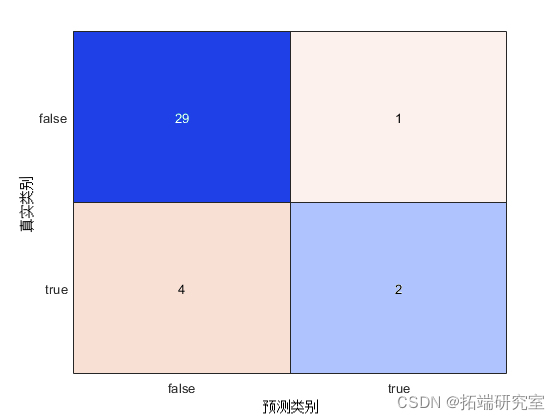
该函数可以正确预测 31 个考试成绩。然而,该函数错误地预测了1名学生获得B或以上的成绩,4名学生获得B以下的成绩。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证 视频讲解|Python图神经网络GNN原理与应用探索交通数据预测
视频讲解|Python图神经网络GNN原理与应用探索交通数据预测 Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据 MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例
MATLAB贝叶斯超参数优化LSTM预测设备寿命应用——以航空发动机退化数据为例


