Box 等人的开创性工作(1994) 在自回归移动平均模型领域的相关工作为波动率建模领域的相关工作铺平了道路,分别由 Engle (1982) 和 Bollerslev (1986) 引入了 ARCH 和 GARCH 模型。
这些模型的扩展包括更复杂的动力学,例如阈值模型来捕捉新闻影响的不对称性,以及除正态之外的分布来解释实践中观察到的偏度和过度峰度。在进一步的扩展中,
本文旨在为单变量 GARCH 过程建模提供一套全面的方法,包括拟合、过滤、预测、模拟以及诊断工具,包括绘图和各种测试。
可下载资源
用于评估模型不确定性的其他方法(例如滚动估计、引导预测和模拟参数密度)为这些过程的建模提供了丰富的环境。
1.价格换对数收益,价格部分最好是GBM
2.garch有自回归,这种假设不太适合出现在收益(和价格上),一般出现在波动率上(如果你假设他有波动率。所以你其实需要的SV模型波动率部分选garch型
3.SV的布朗项指数为一般能选1/2(heston型),1(garch型)和3/2(3/2型)。这三种过程对应波动率对随机因子的缩放程度,可以理解为三种假设(或者观点),选什么看自己风险偏好。 (不过流通比较广的“3/2模型”的均值部分并不是heston型。)
4.如果没有对应产品,这种建模其实是一种对样本内的参数校准(即,对历史样本拟合随机过程的参数)。这个行为本身不是特别建议,特别是对于SV模型的样本内校准,难度很大,准度很差,而且还必须假设某种时间齐次
示例
拟合对象属于 uGARCHfit 类,可以传递给各种其他方法,例如 show (summary)、plot、ugarchsim、ugarchforecast 等。
> fit = ugarchfit(spec = spec)
视频
时间序列分析模型 ARIMA-ARCH GARCH模型分析股票价格数据
视频
什么是Bootstrap自抽样及R语言Bootstrap线性回归预测置信区间
视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现



拟合诊断
稳健标准误差基于 White (1982) 的方法,该方法通过计算参数 (θ) 的协方差 (V) 来生成渐近有效的置信区间:
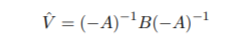
其中,
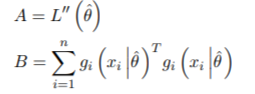
这是最佳分数的Hessian和协方差。稳健标准误差是 V 的对角线的平方根。拟合或过滤对象上的 inforcriteria 方法返回 Akaike (AIC)、贝叶斯 (BIC)、Hannan-Quinn (HQIC) 和 Shibata (SIC) 信息标准,以通过以不同速率惩罚过拟合来启用模型选择。形式上,它们可以定义为:
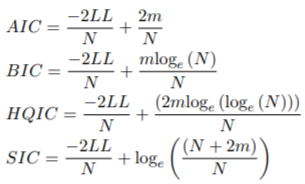
Q-statistics 和 ARCH-LM 检验已被 Fisher 和 Gallagher (2012) 的 Weighted Ljung-Box 和 ARCH-LM 统计量取代,这更好地说明了来自估计模型。ARCH-LM 检验现在是一个加权组合检验,用于检验充分拟合的 ARCH 过程的原假设,而 Ljung-Box 是另一个组合检验,其 ARMA 拟合的充分性为零。signbias 计算 Engle 和 Ng (1993) 的 Sign Bias Test,也显示在摘要中。这测试了标准化残差中杠杆效应的存在(以捕捉 GARCH 模型可能的错误指定),
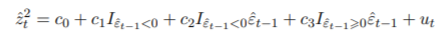
其中 I 是指标函数, ^t 是 GARCH 过程的估计残差。原假设是 H0:ci = 0(对于 i = 1、2、3),并且联合 H0:c1 = c2 = c3 = 0。从先前拟合的总结可以推断,存在显着的负和对冲击的积极反应。使用诸如 apARCH 之类的模型可能会减轻这些影响
gof 计算卡方拟合优度检验,将标准化残差的经验分布与所选密度的理论分布进行比较。
该实现基于 Palm (1996) 的测试,该测试通过重新分类标准化残差而不是根据它们的值(如在标准测试中),而是根据它们的大小,计算在存在非独立同分布观察的情况下的测试,计算观察到小于标准化残差的值的概率,该残差应该是相同的标准均匀分布。该函数必须采用 2 个参数,即拟合对象以及用于对值进行分类的箱数。在拟合摘要中,使用了 (20, 30, 40, 50) 个 bin 的选择,
nymblom 检验计算了 Nyblom (1989) 的参数稳定性检验,以及联合检验。显示用于比较结果的临界值,但在超过 20 个参数的情况下,这不适用于联合测试。
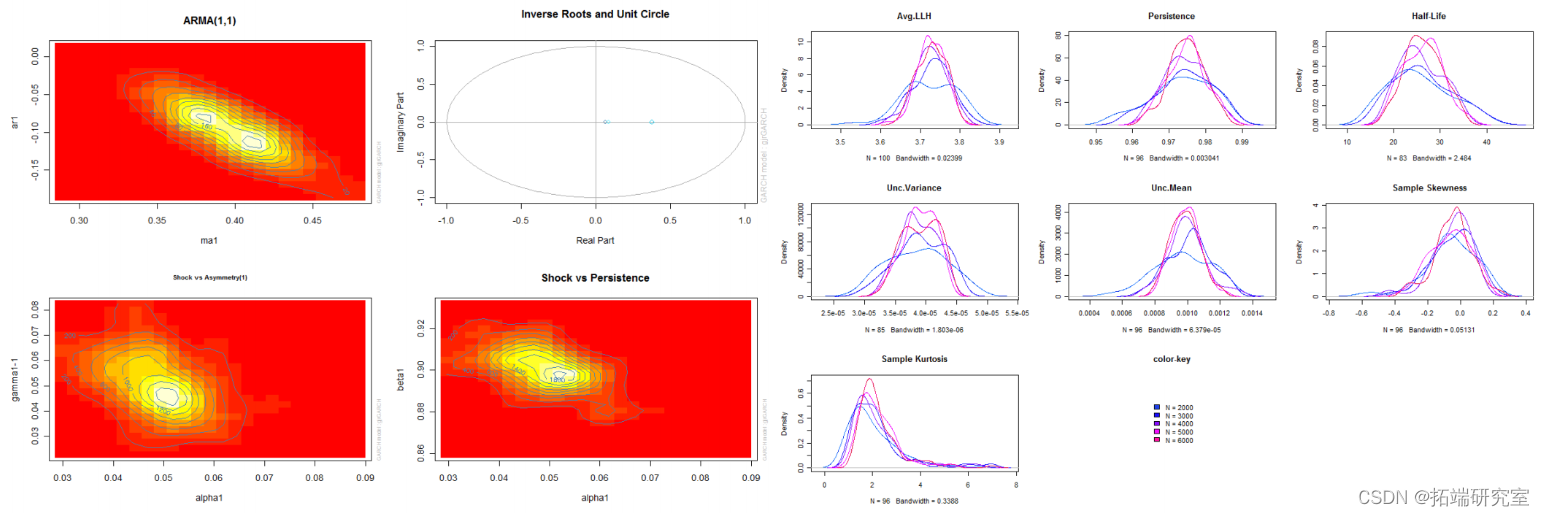
最后,一些信息图可以交互绘制(which = ‘ask’),单独绘制(which = 1:12),或者一次全部绘制(which = ‘all’),如图 2 所示。
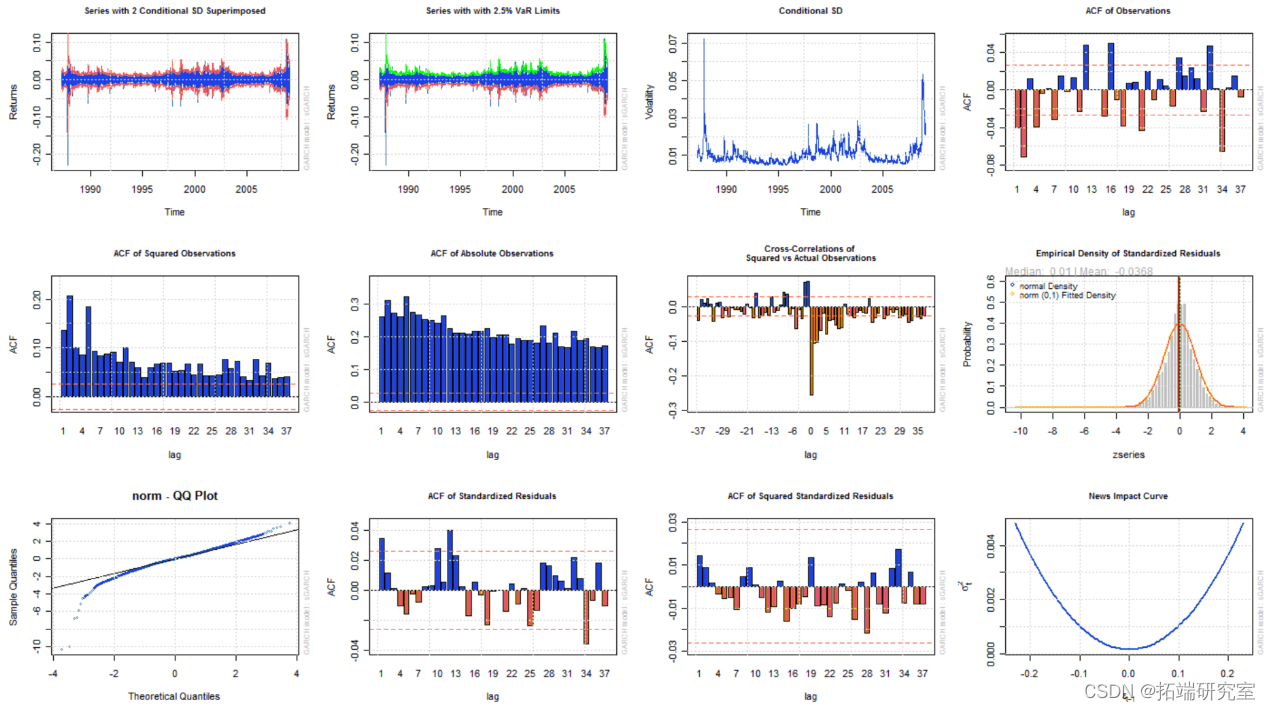
过滤
有时希望使用一组预定义的参数简单地过滤一组数据。例如,当新数据到达并且人们可能不希望重新拟合时,可能就是这种情况。
> filt = ugarchfilter(spec = spe) > show(filt)
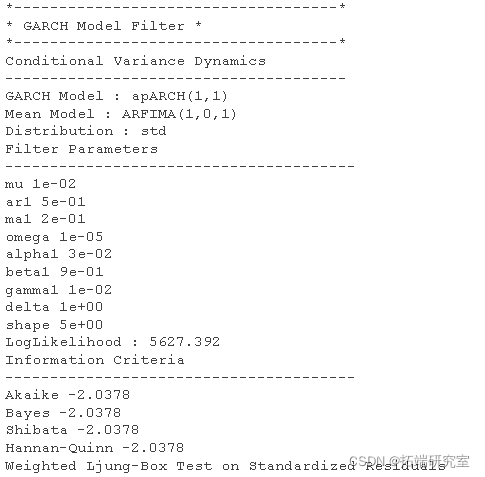
随时关注您喜欢的主题

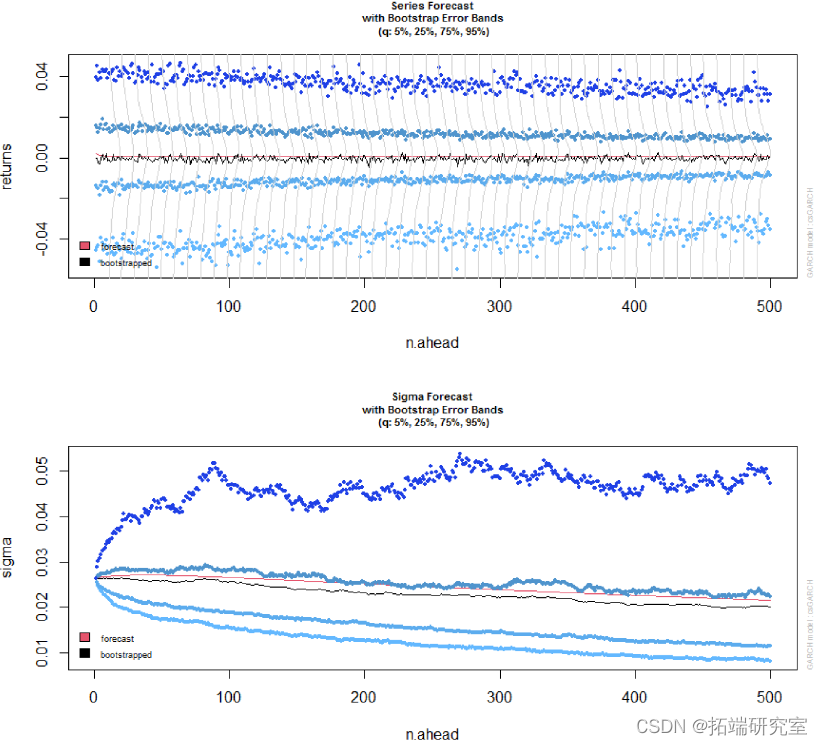
预测和 GARCH bootstrap程序
2 种类型的预测。一种滚动方法,其中基于拟合例程中设置的 out.sample 选项创建连续 1-ahead 预测,以及用于 n>1 超前预测的无条件方法。(也可以将两者结合起来创建一个相当复杂的对象)。在后一种情况下,也可以使用 Pascual 等人描述的 bootstrap程序。 bootstrap 方法基于从拟合模型的经验分布中重新采样标准化残差,以生成序列和 sigma 的未来实现。实现了两种方法:一种通过模拟和重新拟合建立参数的模拟分布来考虑参数不确定性,另一种只考虑分布不确定性,从而避免昂贵且冗长的参数分布估计。
在后一种情况下,1-ahead sigma 预测的预测区间将不可用,因为在这种情况下,只有参数不确定性与 GARCH 类型模型相关。
> sec = ugrspc(are.e=list(model="csGARCH"),ititin="std")
> fi = grit(sc,sp5et)
bot(fit, mehod = c("Pl", "Full")\[1\],
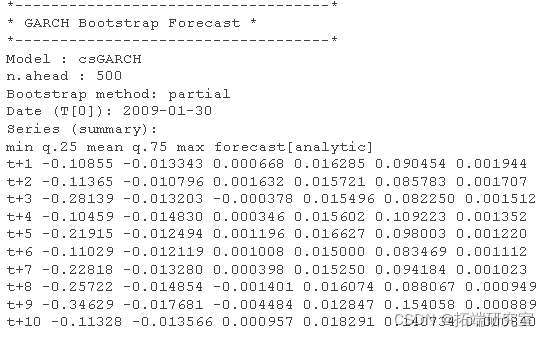
完整 GARCH bootstrap程序总结如下:
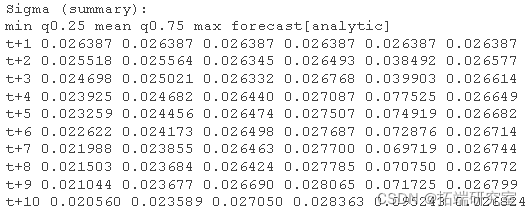
1. 从估计对象中提取标准化残差。如果是具有固定参数的规范,首先使用提供的数据集进行过滤,然后从过滤后的对象中提取标准化残差。
2. 使用 spd 或基于内核的方法从原始标准化残差中采样大小为 N 的 n.bootfit 集(原始数据集减去任何样本周期外)。
模拟
模拟可以直接在拟合对象上进行:

其中 n.sim 表示模拟的长度,而 m.sim 表示独立模拟的数量。出于速度的原因,当 n.sim 相对于 m.sim 较大时,仿真代码在 C 中执行,而对于较大的 m.sim,使用了特殊用途的 C++ 代码(使用 Rcpp 和 RcppArmadillo),发现这会导致速度显着提高。
滚动估计
对模型/数据集组合执行滚动估计和预测,可选择返回指定水平的 VaR。更重要的是,它返回计算预测密度所需的任何度量所必需的分布预测参数。以下示例说明了该方法的使用,其中还使用了并行功能并在 10 个内核上运行。
> cl = mkSluter(10) > spec = uarpc(vaaneoel = list(model = "eGARCH"), ditrtonodel = "jsu") > roll = ghrospe,se .at = 1000, ef.every= 10, refit.windw =moing, calult.V= TRUE, V.ha = c(0.01, 0.05), cser = c, eep.oef = TUE) > report


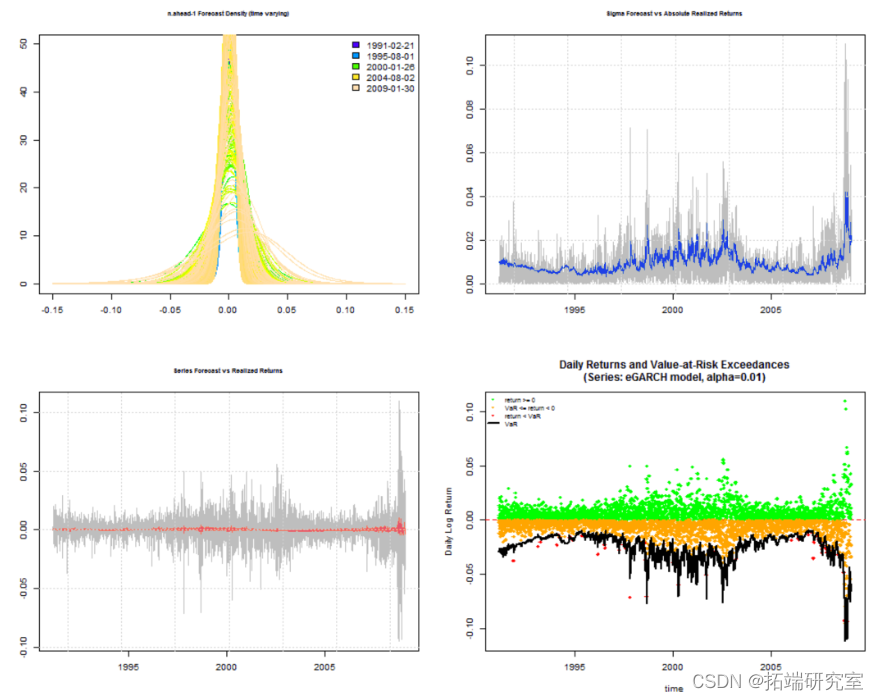
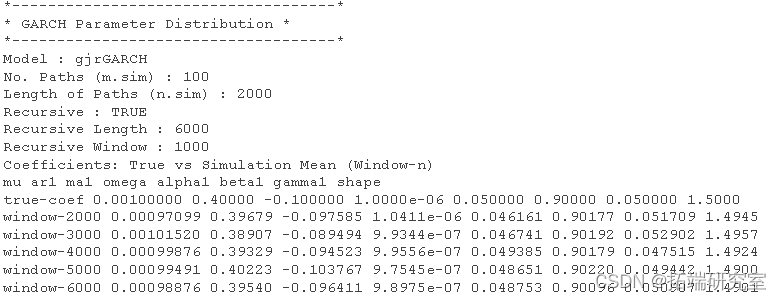
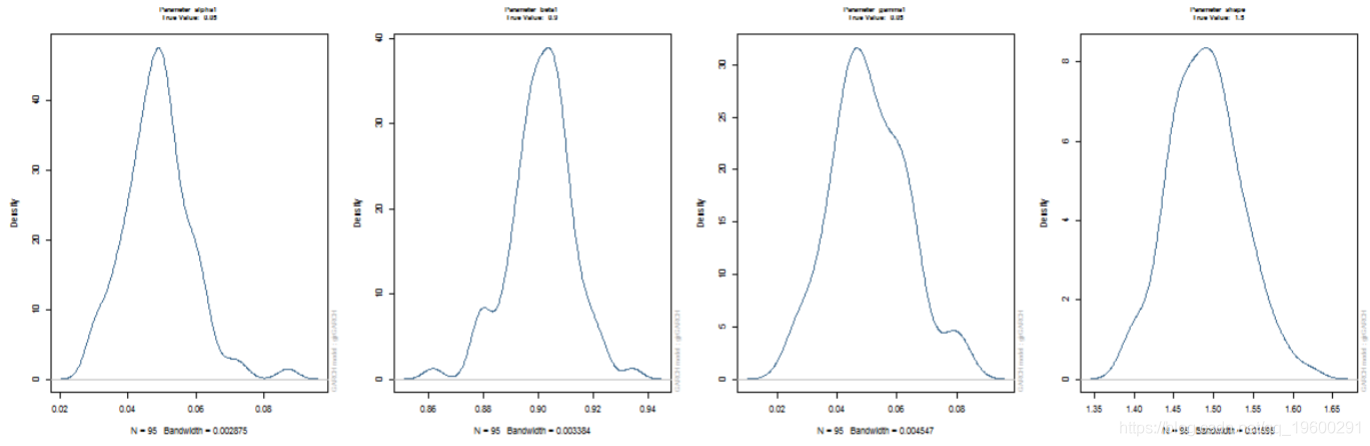
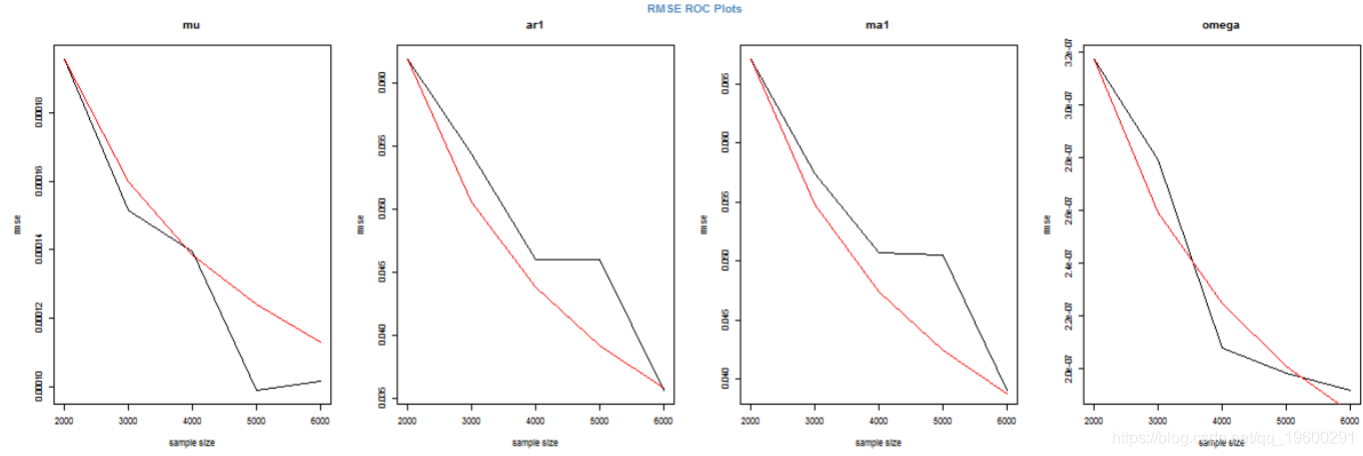
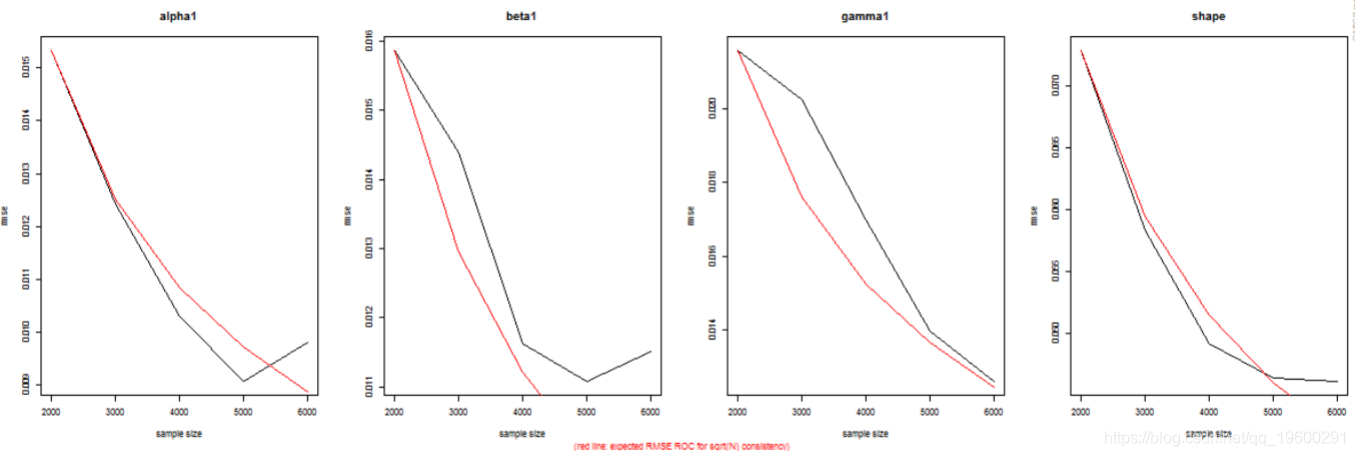
蒙特卡罗实验:模拟参数分布和RMSE
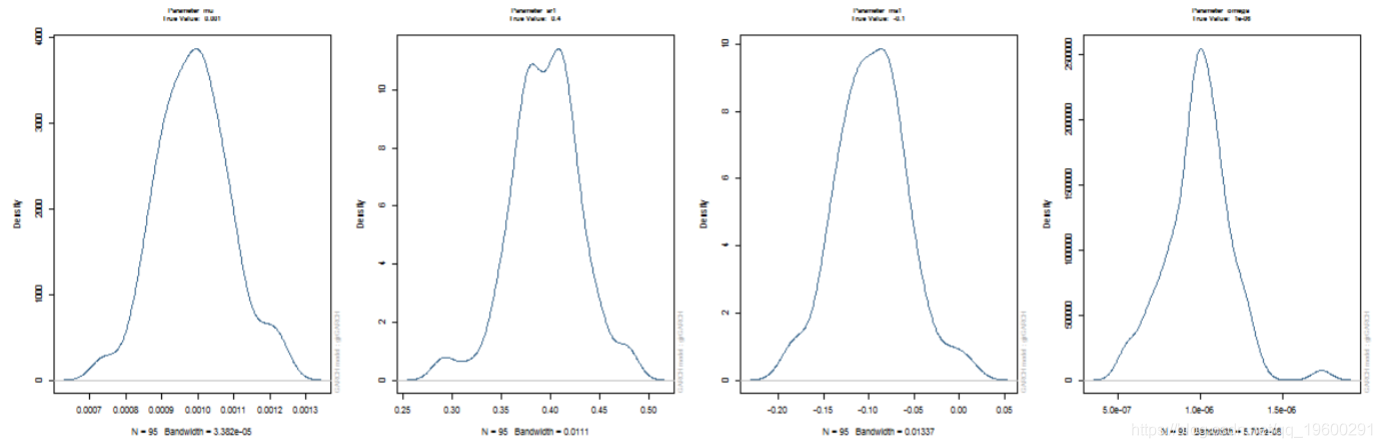
通过多次模拟和拟合模型并针对不同的“窗口”大小来执行蒙特卡罗实验。这允许通过查看均方根误差的下降率以及我们是否具有 √ N 一致性,在数据窗口增加时对参数估计的一致性有所了解。
> spec = urhprnmel = list(model = "gjrGARCH"), + distuto.el "ged") > dist = ugacdsribton(fiOspec spec, n.sm = 2000), + user = cl) > stopCluster(cl) > show(dist)
常见问题解答和指南
问:我应该使用多少数据对 GARCH 过程进行建模?
但是,使用 100 个数据点来尝试拟合模型不太可能是一种合理的方法,因为您不太可能获得非常有效的参数估计。提供了一种方法(ugarchdistribution),用于从预先指定的模型、不同大小的数据进行模拟,将模型拟合到数据,并推断参数的分布以及作为数据长度的 RMSE 变化率增加。这是检查参数分布的一种计算成本非常高的方法(但在非贝叶斯世界中是唯一的方法),因此应谨慎使用并在有足够计算能力的情况下使用。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

 Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码 Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码 【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现 【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例


