
上周在保险课程中,我们了解了广义线性模型的理论
强调了两个重要组成部分
- 链接函数(这实际上是在预测模型的关键)
- 分布或方差函数
可下载资源
考虑数据集
lin.mod = lm(dist~speed,data=cars)
线性模型
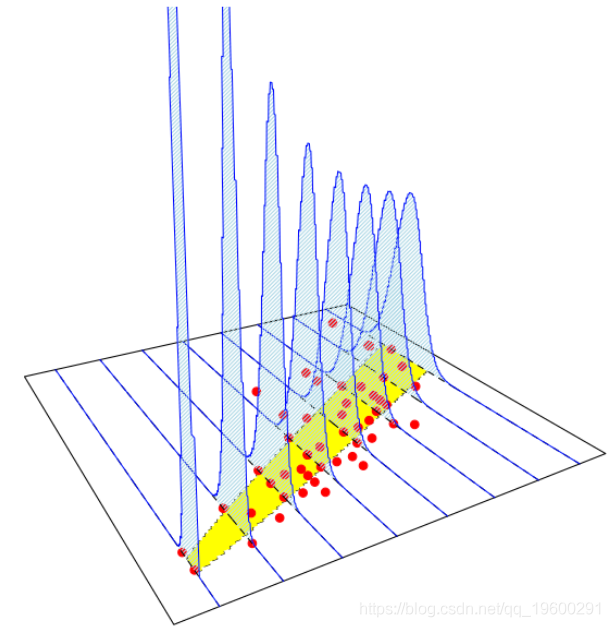
这里的想法(在GLM中)是假设
它将基于某些误差项生成与先前描述的模型相同的模型。该模型可以在下面看到,
C=trans3d(c(x,x),c(y,rev(y)),c(z,z0),mat)
polygon(C,border=NA,col="light blue",density=40)
C=trans3d(x,y,z0,mat)
lines(C,lty=2)
C=trans3d(x,y,z,mat)
lines(C,col="blue")}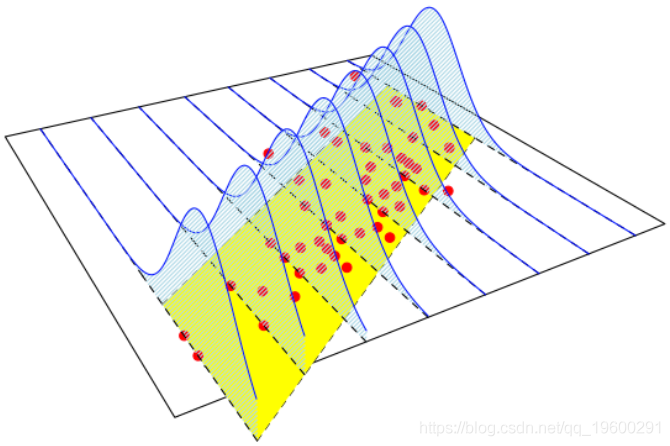
这里确实有两部分:平均值的线性增加 和正态分布的恒定方差
。
另一方面,如果我们假设泊松回归,
poisson.reg = glm(dist~speed,data=cars,family=poisson(link="log"))我们有这样的结果
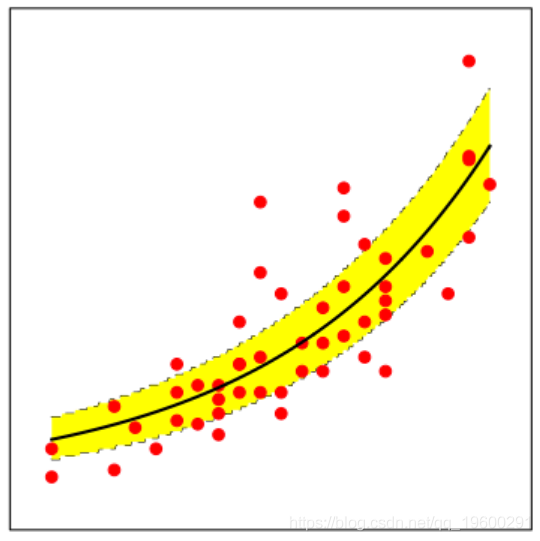
有两件事同时发生了变化:我们的模型不再是线性的,而是指数的,并且方差也随着解释变量的增加而增加
,因为有了泊松回归,
如果改编前面的代码,我们得到
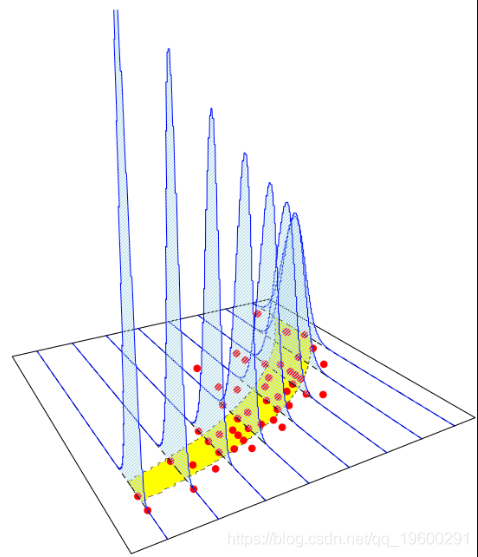
问题是,当我们从线性模型引入Poisson回归时,我们改变了两件事。因此,让我们看看当我们分别更改两个组件时会发生什么。首先,我们可以使用高斯模型来更改链接函数,但是这次是乘法模型(具有对数链接函数)
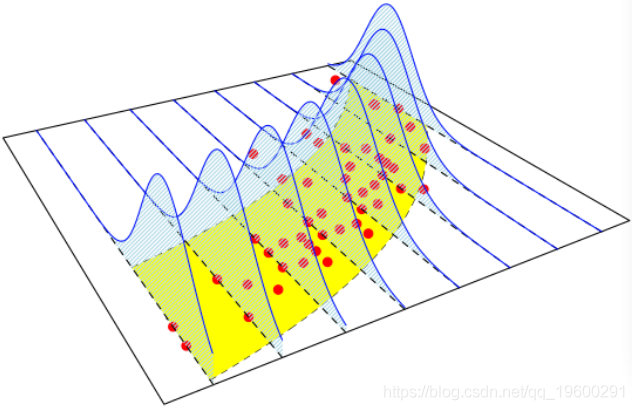
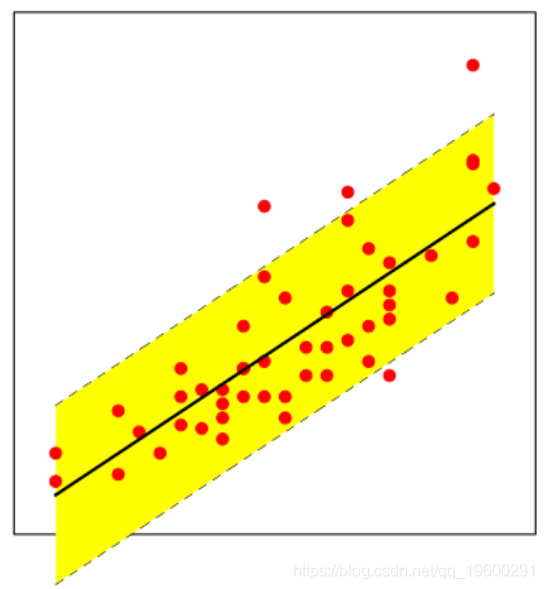
这次是非线性的。或者我们可以在Poisson回归中更改链接函数,以获得线性模型,但异方差
因此,这基本上就是GLM的目的。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载
2026脑机接口行业深度报告:市场规模、产业链、临床进展、政策赋能|附50+份报告PDF、数据、可视化模板汇总下载 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 2026年智旅新纪元AI旅游产业融合全景报告:智慧化、个性化、可持续|附240+份报告PDF、数据、可视化模板汇总下载
2026年智旅新纪元AI旅游产业融合全景报告:智慧化、个性化、可持续|附240+份报告PDF、数据、可视化模板汇总下载 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据



