金融风险管理:VaR 和 ES 的度量
首先明确：1.时间范围-我们展望多少天？2.概率水平-我们怎么看尾部分布？
在给定时间范围内的盈亏预测分布，示例如图1所示。
可下载资源
图1：预测的损益分布
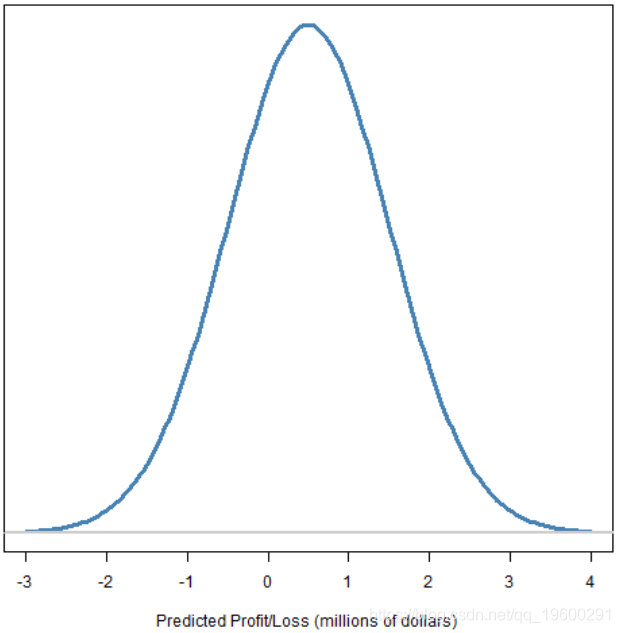
给定概率水平的预测的分位数。
图2：带有分位数的预测损益分布
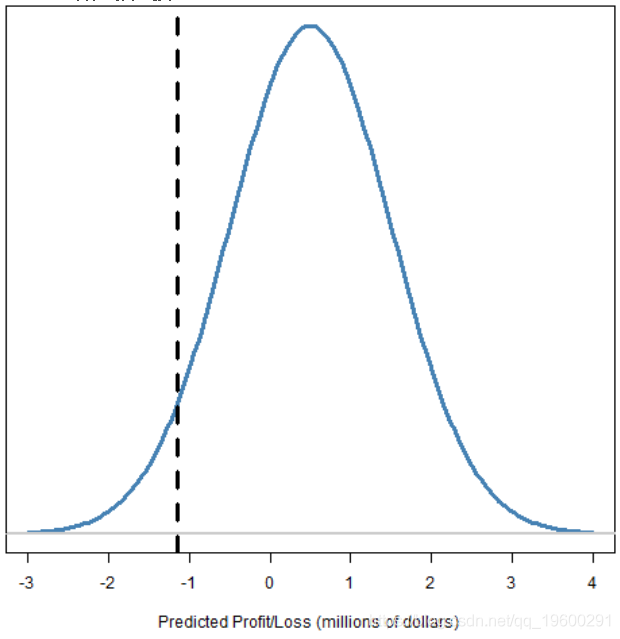
超出分位数的尾部。
图3：带有分位数和尾部标记的预测损益分布
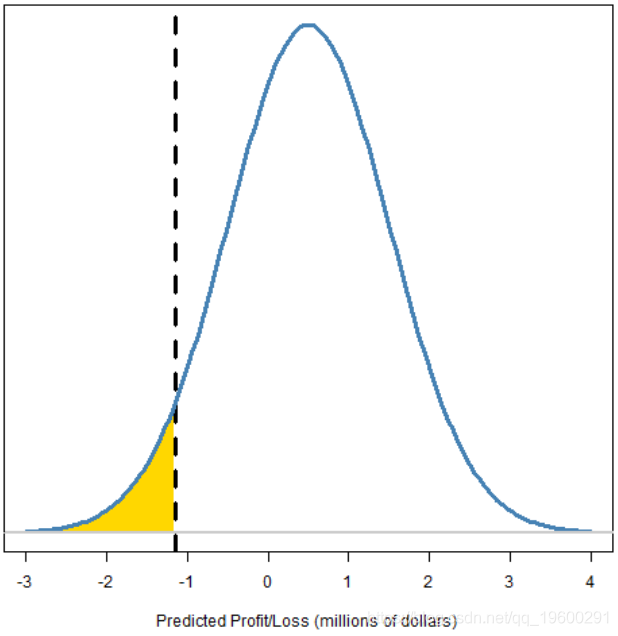
方法
VaR的定义：
风险价值 VaR (Value at Risk)， 是指在一定概率水平（置信水平）下，在一定时间内（如一天，十天等），持有某种证券或投资组合可能遭受的最大损失。
VaR的两个基本要素：置信水平 c，时间段 T
VaR 在概率统计意义上是一个特殊的分位数（Quantile）。（ q th quantile, q = 1 – c. ） 设 L 为损失变量，L = – 收益。当收益为负时，L 为正，则
VaR的优缺点：
优点：简单明了。它直接用货币单位来表示市场风险的大小，即使是没有任何专业背景的投资者或管理者，也能通过 VaR 值对当前市场风险的大小进行评价，方便信息披露，有利于市场监管。
缺点：不满足次可加性（Subadditivity），VaR 对损失或收益变量的尾部分布具体是什么样的一无所知。
我们可以用一个叫尾部均值 （ES）的东西来弥补VaR的不足，它不仅满足次可加性，还刻画了尾部分布的均值（期望值），对 VaR 的功能是一个很好的补充。
ES的定义
尾部均值 ES (Expected Shortfall)，又叫 条件 VaR (Conditional VaR)或 预期尾部损失 ETL (Expected Tail Loss)，是指在损失超过 VaR 的条件下，投资组合遭受的平均损失（期望值）。
计算VaR的几种方法
Delta-normal 方法
假设：
•正态性假设：投资组合中每种资产的收益率都服从正态分布。
•线性假设：投资组合的收益率是各项资产收益率的线性组合。
投资组合每天的收益率相互独立（无相关性）。
一个价值 W_0 元的投资组合，在 c 的置信水平下，在未来 T 天内的 VaR 为：
其中 α 为标准正态分布的q分位数，是一个固定的值。我们可以通过GARCH模型对 σ 进行估计。
GARCH(p, q) 模型假设：
(volatility equation) 其中， ,
历史模拟法，蒙特卡罗模拟法 和 分位数回归法
假设：过去的模式将在一定程度上延续到未来，不会发生改变。
历史模拟法：假设随机变量在未来的分布等同于在过去的分布。
蒙特卡罗模拟法：人为设定随机变量在未来的分布类型（一种特殊的分布，如正态分布、学生 t 分布等），用历史数据估计这种分布的具体参数。
分位数回归是一种特殊的线性回归。
线性回归和分位数回归的主要区别在于被解释变量上。线性回归的被解释变量是期望值，也就是均值。而分位数回归的被解释变量是分位数。
我们可以直接用分位数回归来对分位数进行建模，而对于损失随机变量L来说，分位数其实就是VaR。
风险值（VaR）是在所选概率水平下预测分布分位数的负数。因此，图2和3中的VaR约为110万元。
损失期望值（ES）是超出VaR的尾部预期值的负值（图3中的黄金区域）。因此，它总是比相应的VaR大。
别名
损失期望值
损失期望值有很多别名：
- 条件风险价值（CVaR）
- 平均短缺
- 平均超额损失
我发现“处于风险中的条件价值”令人困惑。我可以看到人们认为在一定条件下它是一种风险价值，而不是超出风险价值的预期损失。
平均超额损失似乎是最具描述性的名称。
在上方，我们看到一个带有多个名称的概念。在下面，我们看到一个具有多个概念的名称。
概率等级
当我说5％时，有人说95％。其实我们都是在处理尾部，这意味着（在我的术语中）肯定少于50％。
缩略语
“风险价值”的缩写有可能与其他两个概念混淆：
- 方差
- 向量自回归
所有这些都可以避免与大写约定冲突：
- VaR：风险价值
- var：方差
- VAR：向量自回归
估算
初始成分
有两种初始成分：
- 投资组合中的资产
- 所涉及资产的价格历史
衍生成分
投资组合加上当前价格得出投资组合权重。
价格历史记录矩阵用于获取退货历史记录矩阵。
plot(xseq, pd, type="l", col="steelblue", lwd=3,
yaxt="n", ylab="",
xlab="Predicted Profit/Loss (millions of dollars)")
abline(v=qnorm(.05, mean=.5, sd=1), lty=2, lwd=3)
polygon(c(xseqt, max(xseqt)), c(dnorm(xseqt,
mean=.5, sd=1), 0), col="gold", border=NA)
lines(xseq, pd, type="l", col="steelblue", lwd=3)
abline(h=0, col="gray80", lwd=2)
投资组合方差计算
给定方差矩阵和权重向量的R命令来获得投资组合方差：
weight %*% varianceMatrix %*% weight
假设权重向量与方差矩阵完全对齐。
weight %*% varianceMatrix[names(weight),
names(weight)] %*% weight风险价值和损失期望值的估计
评估风险价值和损失期望值的简介，以及使用R进行估算 。
基本
风险价值（VaR）和预期短缺（ES）始终与投资组合有关。
您需要两种基本成分：
- 投资组合
- 所涉及资产的价格历史
这些可以用来估计市场风险。价格历史记录中可能不包含其他风险，例如信用风险。
多元估计
当我们从资产级别开始时，VaR和ES在投资组合级别上都是一个风险数字。一种方法是估计资产收益的方差矩阵，然后使用投资组合权重将其折叠为投资组合方差。
单变量估计
通过投资组合的单个时间序列收益（现在是该投资组合），估算更为简单。
随时关注您喜欢的主题
我们可以通过将投资组合中资产的简单收益矩阵乘以投资组合权重的矩阵来获得此信息。
R1 <- assetSimpRetMatrix %*% portWts
或 ：
R1 <- assetSimpRetMatrix[, names(portWts)] %*% portWts
R1上面计算的对象持有投资组合的（假设的）简单收益。
r1 <- log(R1 + 1)
当然，还有其他选择，但是一些常用方法是：
- 历史的（使用最近一段时间内的经验分布）
- 正态分布（根据数据估算参数）并使用适当的分位数
- t分布（通常假设自由度而不是估计自由度）
- 拟合单变量garch模型并提前进行模拟
R分析
以下是示例，其中spxret11包含2011年标准普尔500指数每日对数收益的向量。因此，我们将获得2012年第一天的风险度量（收益）。
> "historical")
[,1]
VaR -0.02515786
> "gaussian")
[,1]
VaR -0.0241509
> "gaussian"
[,1]
VaR -0.03415703
> "historical")
[,1]
ES -0.03610873
> "gaussian")
[,1]
ES -0.03028617如果第一个参数是矩阵，则每一列都可以视为投资组合中的资产。
no weights passed in, assuming equal weighted portfolio
$MVaR
[,1]
[1,] 0.02209855
$contribution
Convertible Arbitrage CTA Global
0.0052630876 -0.0001503125
Distressed Securities Emerging Markets
0.0047567783 0.0109935244
Equity Market Neutral
0.0012354711
$pct_contrib_MVaR
Convertible Arbitrage CTA Global
0.238164397 -0.006801916
Distressed Securities Emerging Markets
0.215252972 0.497477204
Equity Market Neutral
0.055907342这是用于风险价值的历史估计的简单函数的定义：
风险价值的历史估计
VaRhistorical <- function(returnVector, prob=.05,
notional=1, digits=2)
{
if(prob > .5) prob <- 1 - prob
ans <- -quantile(returnVector, prob) * notional
signif(ans, digits=digits)
}投资组合，例如：
> VaRhistorical(spxret11, notional=13e6)
5%
330000损失期望值 ：
EShistorical <- function(returnVector, prob=.05,
notional=1, digits=2)
{
可以这样使用：
> EShistorical(spxret11, notional=13e6)
[1] 470000
因此，风险价值为 330,000，损失期望值为 470,000。
正态分布
稍后会有一个更好的版本（从统计意义上来说），但是这是一种假设正态分布来获得“风险价值”的简单方法：
用法如下：
> VaRnormalEqwt(spxret11, notional=13e6)
[1] 310000
> VaRnormalEqwt(spxret11, notional=13e6,
+ expected.return=0)
[1] 310000在这种情况下，计算损失期望值有点复杂，因为我们需要找到尾部的期望值。
ESnormalEqwt <- function(returnVector, prob=.05,
notional=1, expected.return=mean(returnVector),
digits=2)
{
ans <- -tailExp * notional
signif(ans, digits=digits)
这个例子的结果是：
> ESnormalEqwt(spxret11, notional=13e6)
[1] 390000VaRnormalExpsmo <- function(returnVector, prob=.05,
notional=1, expected.return=mean(returnVector),
lambda=.97, digits=2)
{
signif(ans, digits=digits)
一个更好的办法是用指数平滑得到的波动性：
其中pp.exponential.smooth取自“指数衰减模型”。
> VaRnormalExpsmo(spxret11, notional=13e6)
[1] 340000t分布
VaRtExpsmo <- function(returnVector, prob=.05,
notional=1, lambda=.97, df=7, digits=2)
{
if(prob > .5) prob <- 1 - prob
结果是：
> VaRtExpsmo(spxret11, notional=13e6)
2011-12-30
340000可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言VAR模型的多行业关联与溢出效应可视化分析
马尔可夫转换MSVAR模型预测资产收益率时间序列可视化分析|附数据代码
R语言软件套保期限GARCH VAR模型对沪深300金融数据可视化分析
R语言交互可视化分析房屋市场：arima、VAR时间序列、XGBoost、主成分分析、LASSO可视化报告
