大多数数据都可以用数字来衡量,如身高和体重。
然而,诸如性别、季节、地点等变量则不能用数字来衡量。相反,我们使用虚拟变量来衡量它们。
例子:性别
让我们假设x对y的影响在男性和女性中是不同的。
对于男性y=10+5x+ey=10+5x+e
对于女性y=5+x+ey=5+x+e。
虚拟变量(dummy variable)也叫哑变量,翻译不同而已。因为dummy的含义有假的、虚拟的、哑的等各种含义,所以国内翻译也不一样。但是他们俩是一回事。
虚拟变量其实算不上一种变量类型(比如连续变量、分类变量等),确切地说,是一种将多分类变量转换为二分变量的一种形式。Dummy这个词意思是虚拟的、假的,所以dummy variable意思就是假的变量,不是真实的变量。那它到底虚拟在什么地方呢?我们通过一个例子来详细解释一下。
例:某研究者检测了四种不同类型社区(分别用0、1、2、3表示)的SO2情况。研究者欲分析社区类型是否与SO2水平有关系,或者说,不同社区类型的SO2水平是否不同。
该例子中,因变量SO2水平是一个定量资料,自变量社区类型是一个分类资料,分析方法可以考虑一般线性模型。
首先要强调一点,不管是一般线性模型还是广义线性模型,它们都是“线性”的,也就是说,只要你采用了这些模型,就已经默认了自变量与因变量之间的关系是线性的。
所谓虚拟变量,就是把原来的一个多分类变量转化为多个二分变量,总的来说就是,如果多分类变量有k个类别,则可以转化为k-1个二分变量。如变量x为赋值1、2、3、4的四分类变量,就可以转换为3个赋值为0和1的二分类变量。
在进一步解释虚拟变量的含义之前,我们需要先了解一下“参照”的含义。分类结果的解释一般是要有参照类别的。比如我们说男性肺癌发生率高,暗含了“相对女性”这样的参照;50岁以上人群冠心病发生率更高,暗含了“相对50岁以下人群”的参照。没有参照,就没法说高或低。比如我们单独说80%这个数字,它是高还是低呢?相对70%就是高的,相对90%就是低的。所以分类变量的结果需要结合参照来解释。
当我们把k个类别的多分类变量转化为k-1个二分变量后,每一个二分类变量表示相对参照类的大小。例如,多分类变量x用1、2、3、4表示,我们设定以1作为参照,那么生成的3个虚拟变量分别表示:2和1相比的大小、3和1相比的大小、4和1相比的大小。
通过生成虚拟变量,就把原来的一个系数变成了多个系数,这多个系数更详细地显示了自变量与因变量之间的关系,尤其在非线性关系的时候,尤其重要。因为当你在用线性回归、logistic回归这些方法的时候,已经默认了是线性关系了,你是不可能找出非线性关系的。
如何设置虚拟变量呢?目前大多数软件都可以实现,如SAS软件在各种回归分析的过程中,一般都会有class语句,通过class语句的param=reference选项便可实现虚拟变量的设置。在SPSS中,在回归分析界面可以点击Categorical,通过该按钮可以设置虚拟变量,并指定其参照类。
最后强调一点:在模型分析时,虚拟变量都是同进同出,也就是说,要么都在模型中,要么都不在模型中,不能只保留其中一个,否则它的含义就变了。
其中e是随机效应,平均值为零。因此,在y和x的真实关系中,性别既影响截距又影响斜率。
首先,让我们生成我们需要的数据。
#真斜率,男性=5,女性=1
ifelse(d$性别==1, 10+5*d$x+e,5+d$x+e)首先,我们可以看一下x和y之间的关系,并按性别给数据着色。
plot(data=d)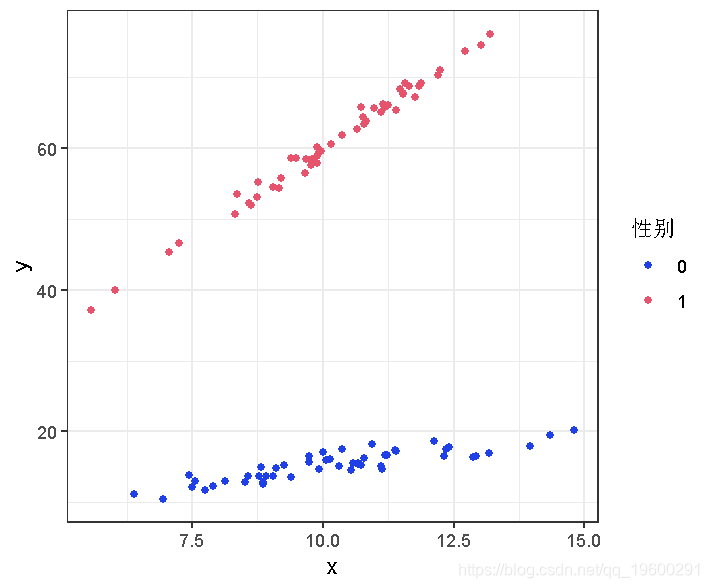
很明显,y和x之间的关系不应该用一条线来描绘。我们需要两条:一条代表男性,一条代表女性。
如果我们只将y回归到x和性别上,结果是

x的估计系数不正确。
正确的设置应该是这样的,这样可以使性别同时影响截距和斜率。
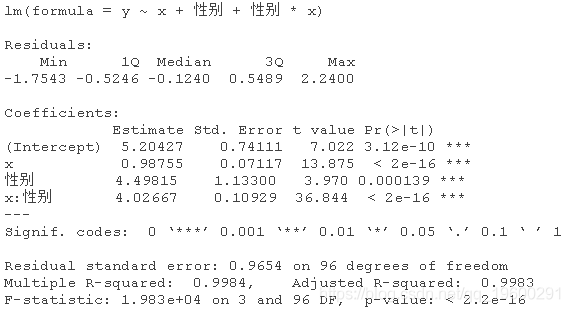
或者使用下面的方法,添加一个虚拟变量。
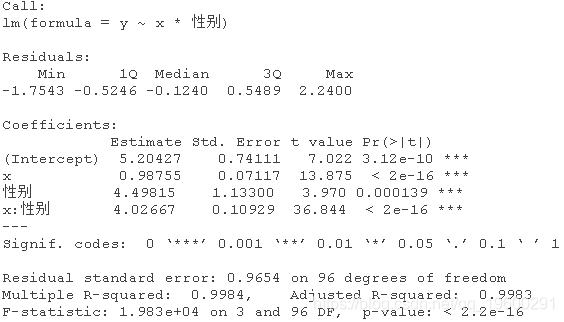
该模型表示,对于女性(性别=0),估计的模型是y=5.20+0.99x;对于男性(性别=1),估计的关系是y=5.20+0.99x+4.5+4.02x,也就是y=9.7+5.01x,相当接近真实关系。
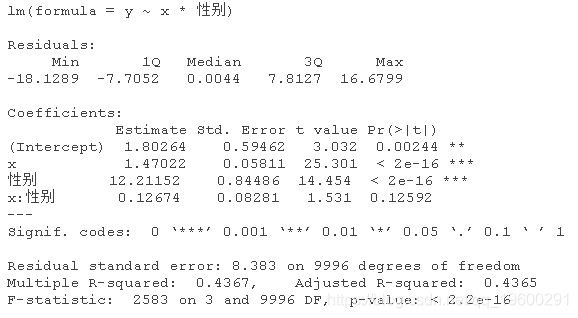
接下来,让我们尝试两个虚拟变量:性别和地点
性别和地点的虚拟变量
性别并不重要,但地点很重要
让我们获取一些数据,其中性别不重要,但地点会很重要。
绘制查看x和y之间的关系,按性别给数据着色,并按地点分开。
plot(d,grid~location)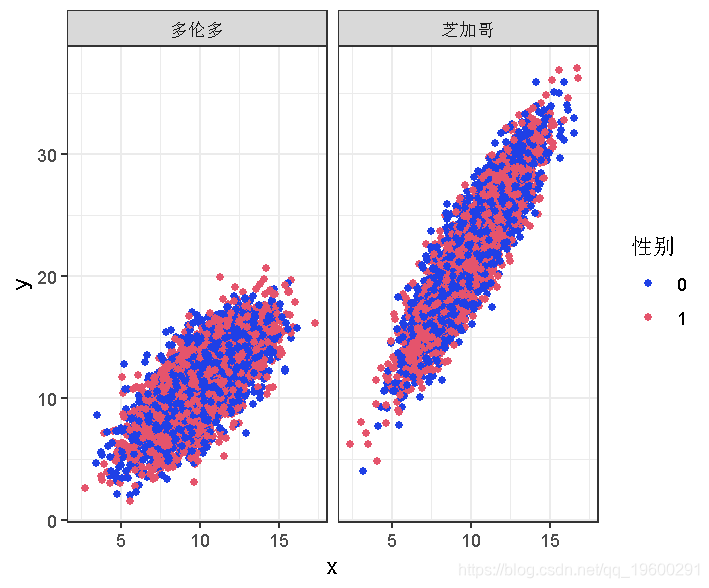
随时关注您喜欢的主题
性别对Y的影响似乎是显著的。但当你比较芝加哥的数据和多伦多的数据时,截距不同,斜率也不同。
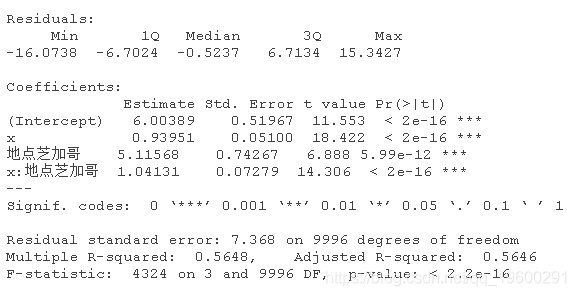
如果我们忽略了性别和地点的影响,模型将是
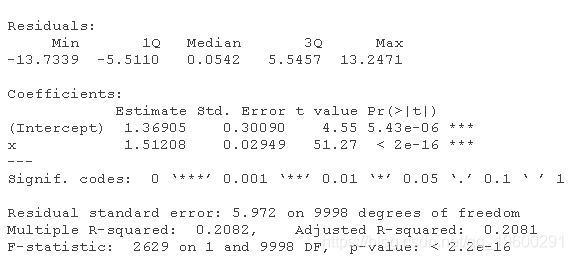
R-squared是相当低的。
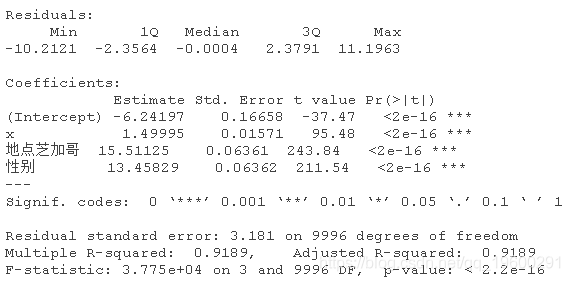
我们知道性别并不重要,但我们还是把它加进去,看看是否会有什么不同。
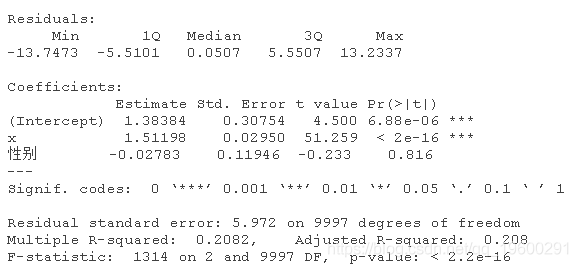
正如预期,性别的影响并不显著。
现在让我们来看看地点的影响

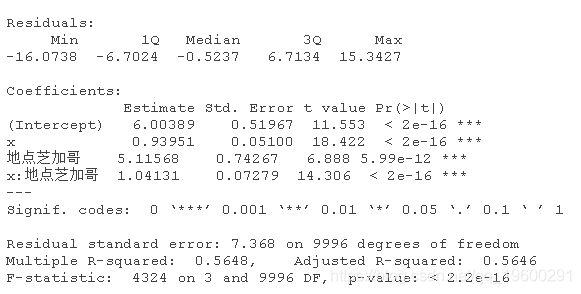
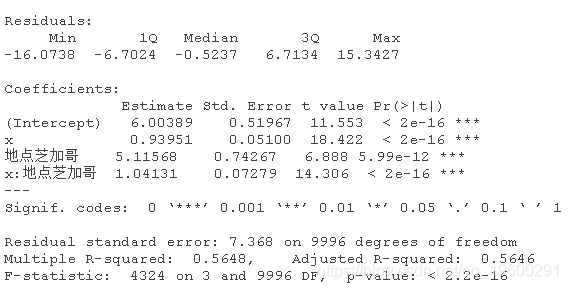
位置的影响是很大。但我们的模型设置基本上是说,位置只会改变截距。
如果位置同时改变了截距和斜率呢?

你也可以试试这个。

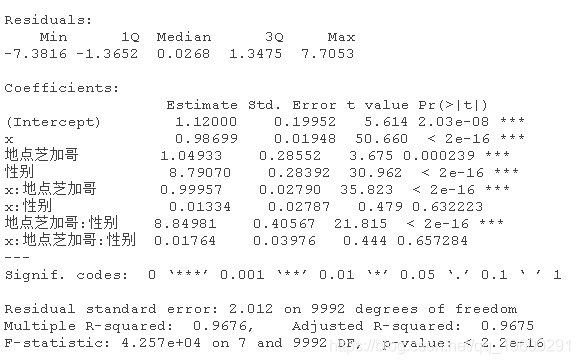
性别并不重要,而地点会改变截距和斜率。
性别并不重要,而地点会改变截距和斜率
ifelse(d$性别=="0" & d$地点=="多伦多", 1+1*d$x+e,
+ ifelse(d$性别=="1" & d$地点=="芝加哥", 20+2*d$x+e,
+ ifelse(d$性别=="0" & d$地点=="芝加哥", 2+2*d$x+e,NA))))现在让我们获取一些性别和地点都很重要的数据。让我们从两个地点开始。
plot(d,x,y,color=性别~地点)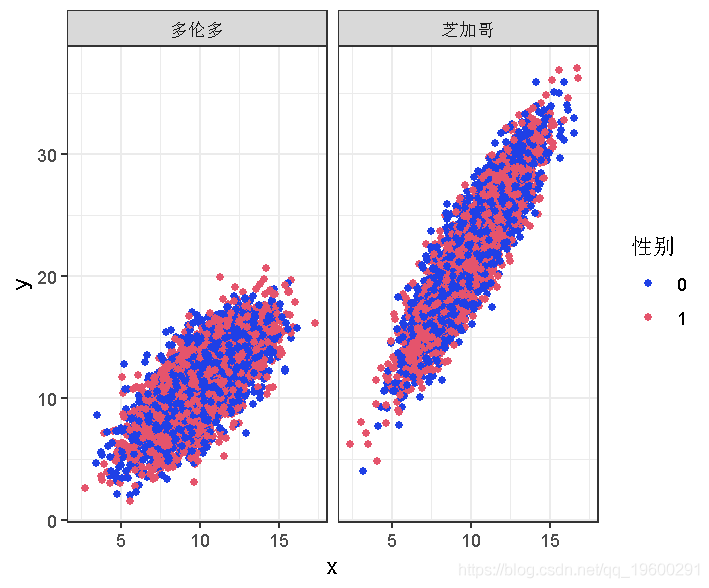


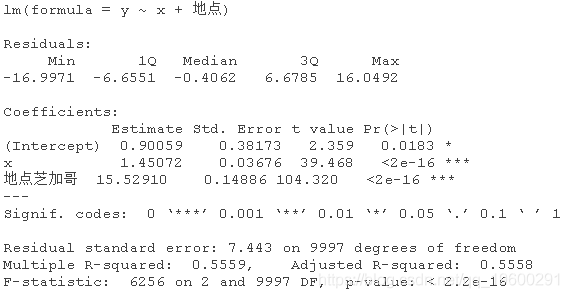
性别和地点都很重要,5个地点
最后,让我们尝试一个有5个地点的模型。
+ ifelse(d$性别=="1" & d$地点=="芝加哥", 2+10*d$x+e,
+ ifelse(d$性别=="0" & d$地点=="芝加哥", 2+2*d$x+e,
+ ifelse(d$性别=="1" & d$地点=="纽约",3+15*d$x+e,
+ ifelse(d$性别=="0" & d$地点=="纽约",3+5*d$x+e,
+ ifelse(d$性别=="1" & d$地点=="北京",8+30*d$x+e,
+ ifelse(d$性别=="0" & d$地点=="北京",8+2*d$x+e,
+ ifelse(d$性别=="1" & d$地点=="上海",plot( x,y,color=性别 ~地点)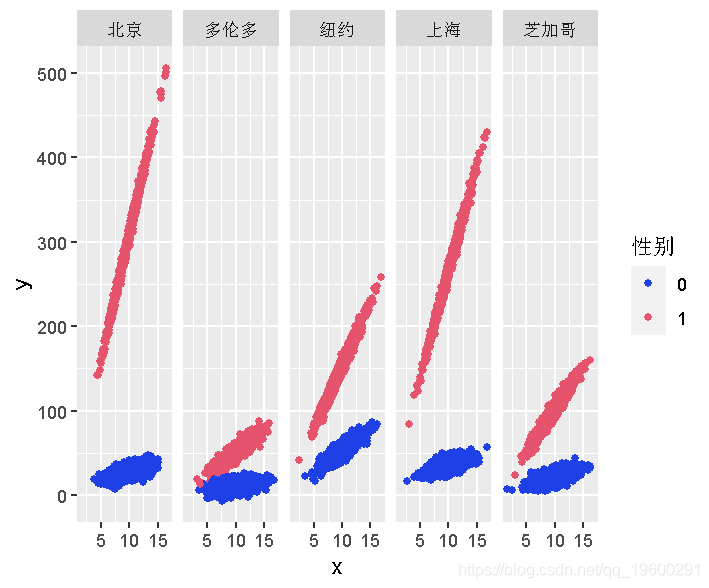
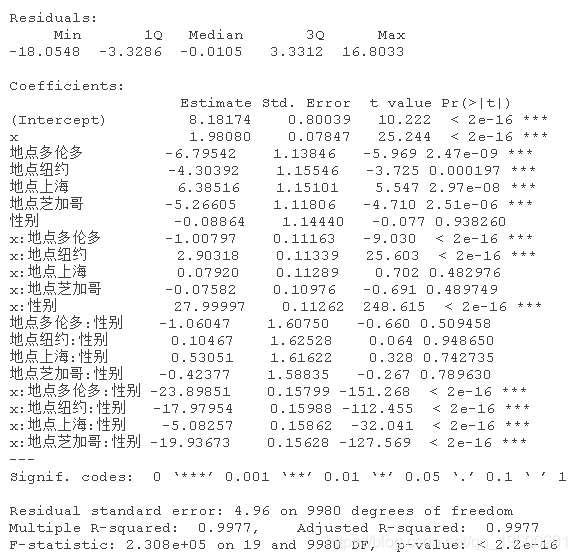
所以,如果你认为某些因素(性别、地点、季节等)可能会影响你的解释变量,就把它们设置为虚拟变量。

可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据
Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据 专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据 Stata智慧城市建设对经济高质量发展的影响面板数据分析:超效率SBM模型引入中介变量及空间杜宾模型SDM
Stata智慧城市建设对经济高质量发展的影响面板数据分析:超效率SBM模型引入中介变量及空间杜宾模型SDM Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究
Python谷歌商店Google Play APP评分预测:LASSO、多元线性回归、岭回归模型对比研究



