
目前,回归诊断不仅用于一般线性模型的诊断,还被逐步推广应用于广义线性模型领域(如用于logistic回归模型)。
但由于一般线性模型与广义线性模型在残差分布的假定等方面有所不同,所以推广和应用还存在许多问题。
鉴于此,本文使用图表考察logistic模型的拟合优度。如何处理从逻辑回归中得到的残差图? 为了更好地理解,让我们考虑以下数据集
glm(Y~X1+X2,family=binomial)如果我们使用R的诊断图,第一个是残差的散点图,对照预测值。
残差图是指以残差为纵坐标,以任何其他指定的量为横坐标的散点图。(上图仅是残差的示意图,非残差图,残差图可见下文)
用普通最小二乘法(OLS)做回归分析的人都知道,回归分析后的结果一定要用残差图(residual plots)来检查,以验证你的模型。你有没有想过这究竟是为什么?残差图又究竟是怎么看的呢?
这背后当然有数学上的原因,但是这里将着重于聊聊概念上的理解。从根本上说,随机性(randomness)和不可预测性(unpredictability)是任何回归模型的关键组成部分,如果你没有考虑到这两点,那么你的模型就不可信了,甚至说是无效的。
为什么这么说呢?首先,对于一个有效的回归模型来说,可以细分定义出两个基本组成部分:
Response =(Constant + Predictors)+ Error
我想说的是另一种说法,那就是:
响应(Response) = 确定性(Deterministic) + 随机性(Stochastic)
(有时候真是不得不吐槽下,毕竟是外国人发明的现代科学,中文翻译过来难眠有混淆视听之嫌,学术词汇的理解还是看英文更能清晰本质,一会就会聊到Stochastic就明白为什么这么说)
确定性部分(The Deterministic Portion)
为了完整,先提一下Deterministic这部分。在预测模型中,该部分是由关于预测自变量的函数组成,其中包含了回归模型中所有可解释、可预测的信息。
随机误差(The Stochastic Error)
Stochastic 这个词很牛逼,其不仅蕴含着随机性(random),还有不可预测性(unpredictable)。这是很重要的两点,往往很多朋友都以为有随机性的特点就够了,其实不然。这两点放在一起,就是在告诉我们回归模型下的预测值和观测值之间的差异必须是随机不可预测的。换句话说,在误差(error)中不应该含有任何可解释、可预测的信息。
模型中的确定性部分应该是可以很好的解释或预测任何现实世界中固有的随机响应。如果你在随机误差中发现有可解释的、可预测的信息,那就说明你的预测模型缺少了些可预测信息。那么残差图(residual plots)就可以帮助你检查是否如此了!
> plot(reg,which=1)也可以
> plot(predict(reg),residuals(reg))
> abline(h=0,lty=2 )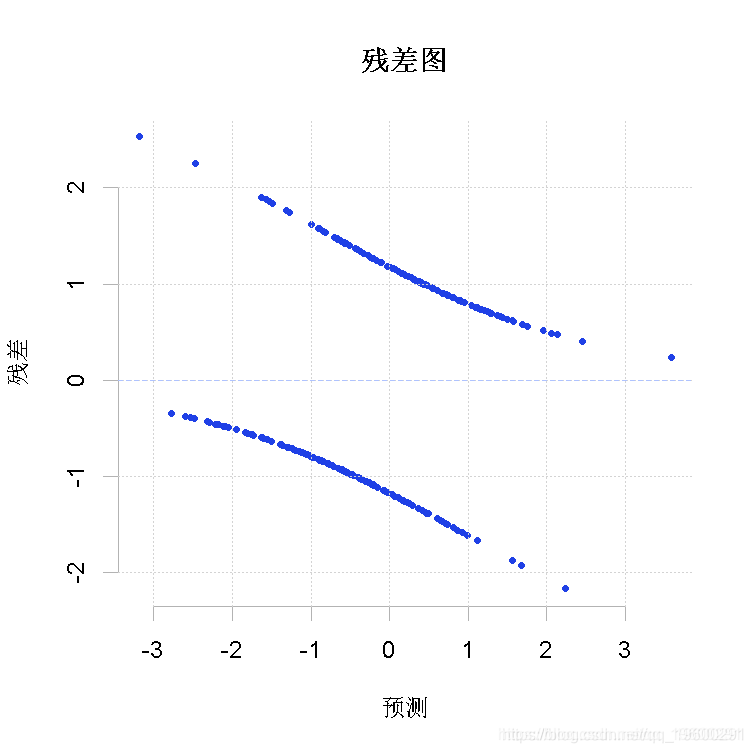
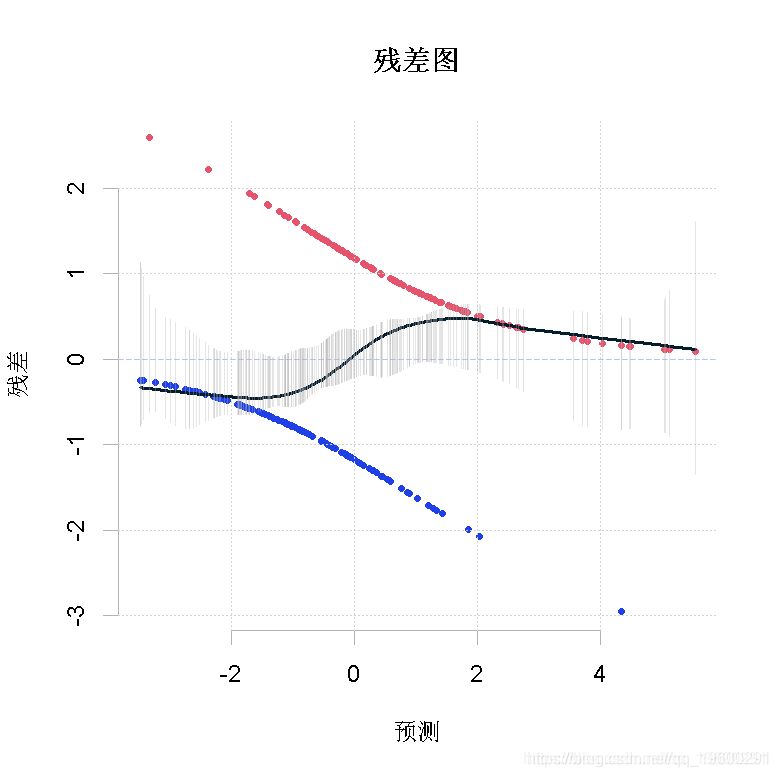
为什么我们会有这两条线的点?因为我们预测了一个变量取值为0或1的概率。当我们使用彩色时,可以更清楚地看到,如果真值是0,那么我们总是预测得更多,残差必须是负的(蓝点),如果真值是1,那么我们就低估了,残差必须是正的(红点)。当然,还有一个单调的关系
> plot(predict(reg),residuals(reg) )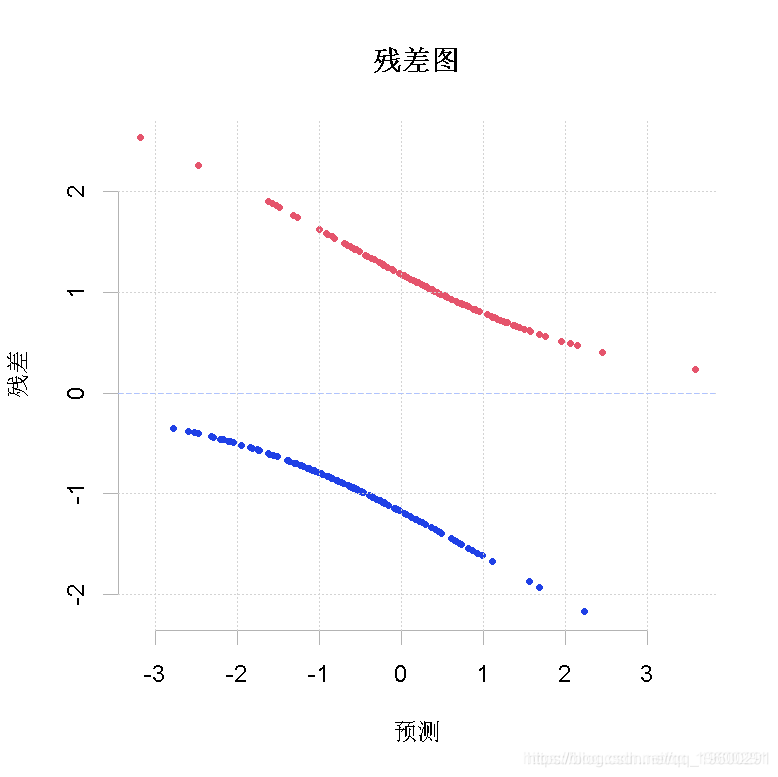
点正好在一条平滑的曲线上,是预测值的一个函数。
现在,从这个图上看不出什么。我们运行一个局部加权回归,看看发生了什么。
lowess(predict(reg),residuals(reg)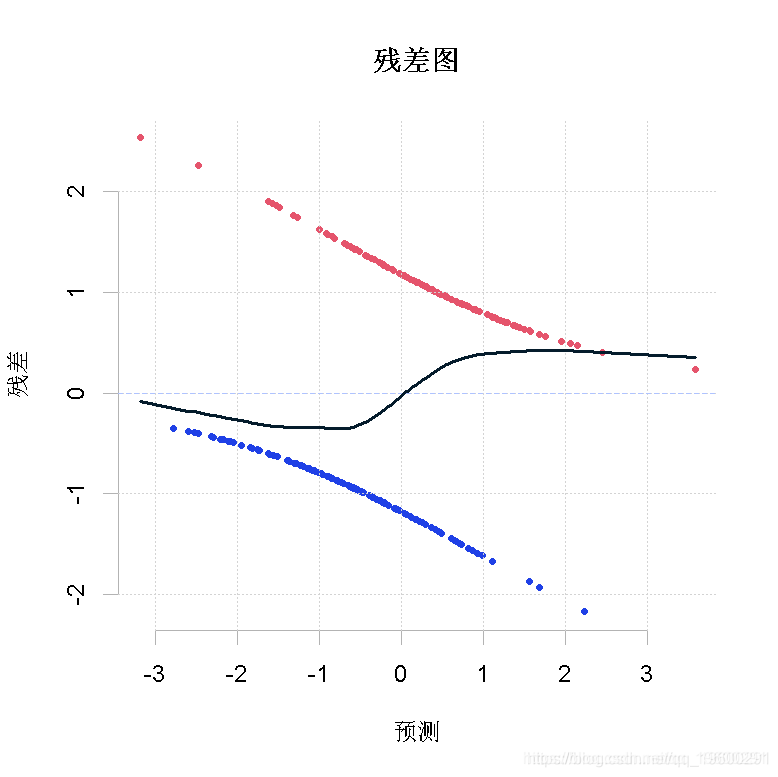
这是我们在第一个诊断函数中所得到的。但在这个局部回归中,我们没有得到置信区间。我们可以假设图中水平线非常接近虚线吗?
segments( fit+2* se.fit, fit-2* se.fit )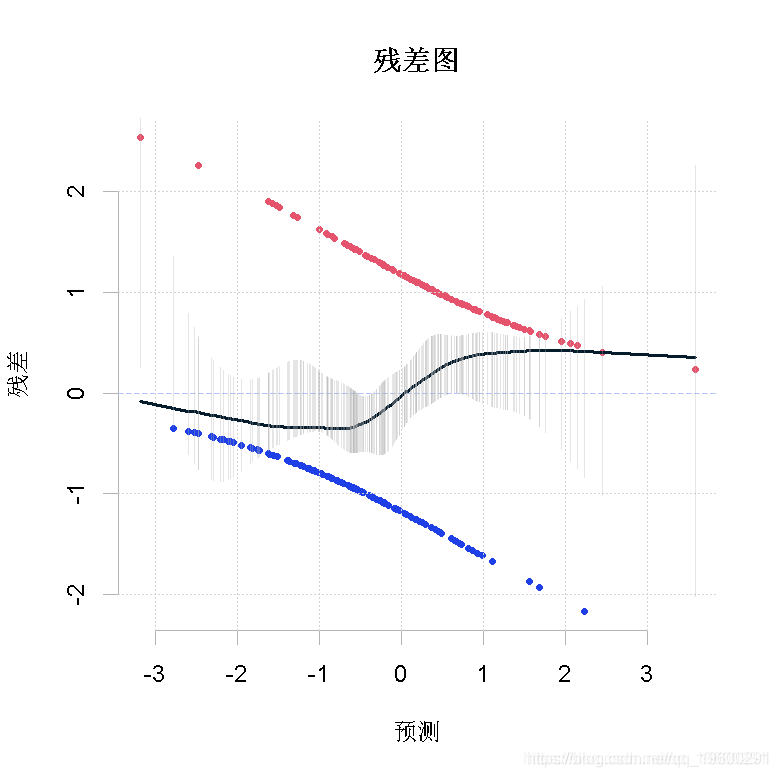
可以。这个图表表明什么?
事实上,该图可能不是观察残差的唯一方法。如果不把它们与两个解释变量绘制在一起呢?例如,如果我们将残差与第二个解释变量作对比,我们会得到
> lines(lowess(X2,residuals(reg))随时关注您喜欢的主题
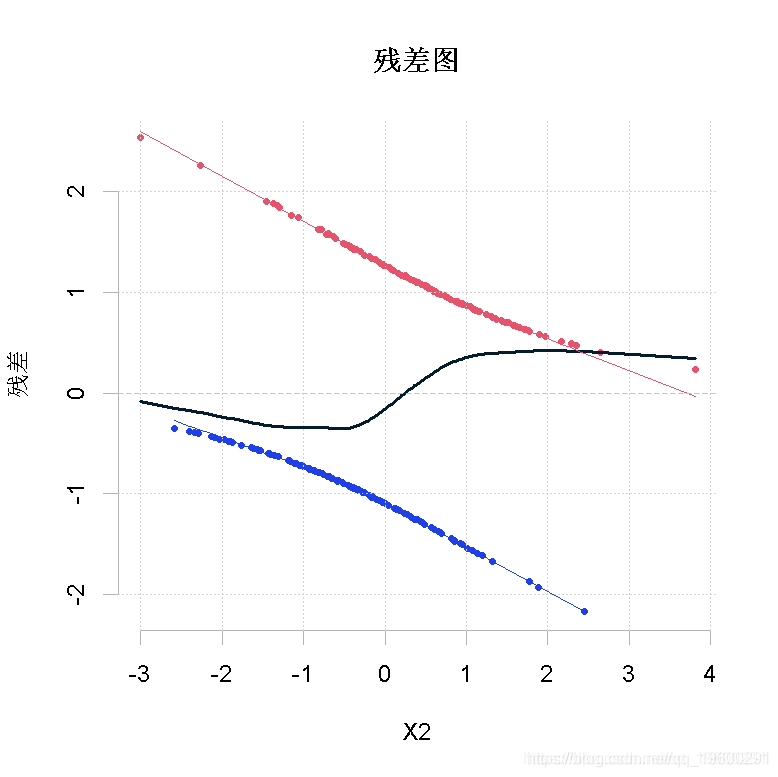
对照一下,该图与我们之前的图相似。
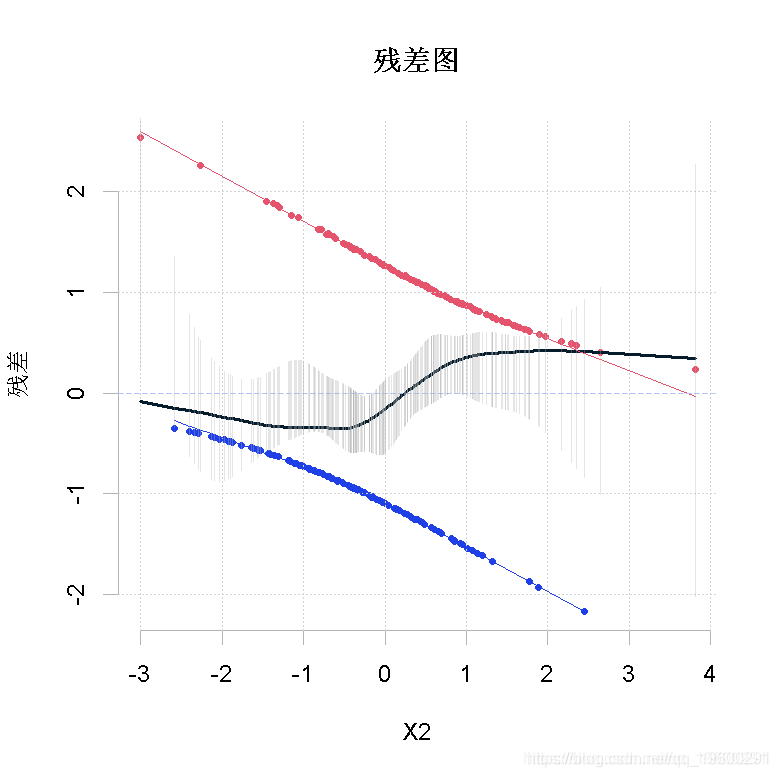
如果我们现在看一下与第一个解释变量的关系:
> lines(lowess(X1,residuals(reg))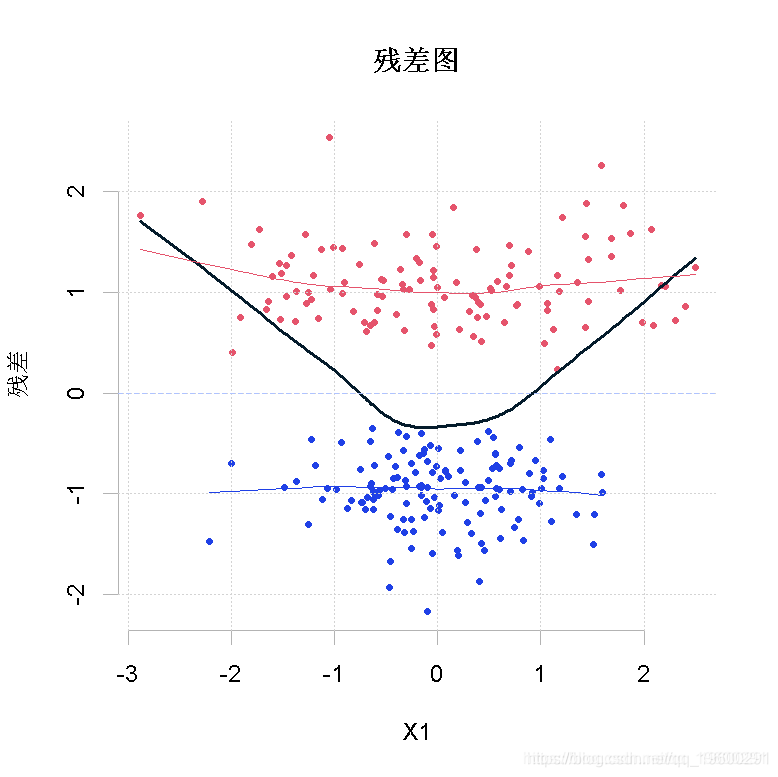
因为我们可以清楚地识别出二次方的影响。这张图表明,我们应该对第一个变量的平方进行回归。而且可以看出它是一个重要的影响因素。
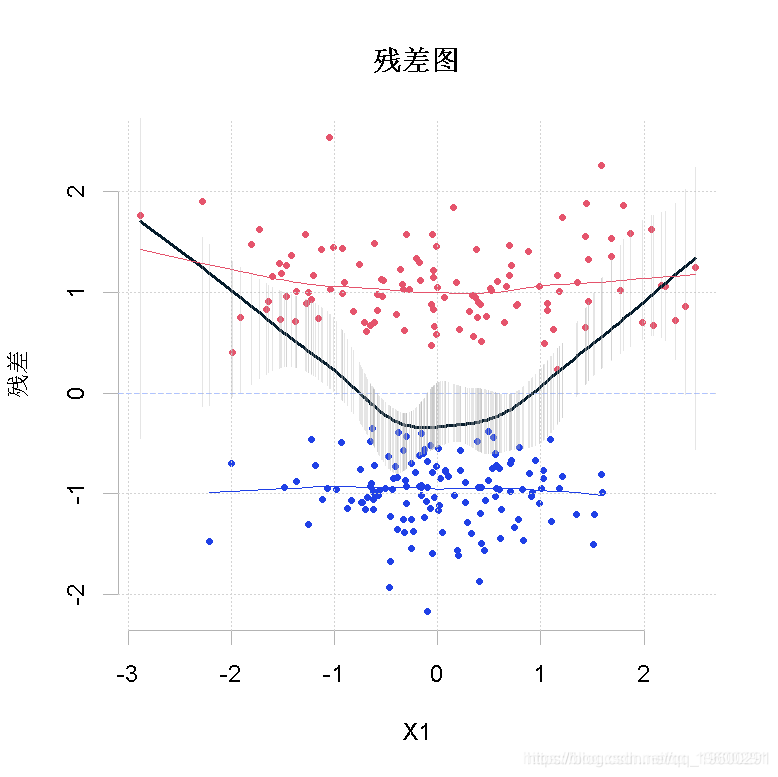
现在,如果我们运行一个包括这个二次方效应的回归,我们会得到什么。
glm(Y~X1+I(X1^2)+X2,family=binomial)看起来和第一个逻辑回归模型结果类似。
那么本文的观点是什么?观点是
- 图形可以用来观察可能出错的地方,对可能的非线性转换有更多的直觉判断。
- 图形不是万能的,从理论上讲,残差线应该是一条水平的直线。但我们也希望模型尽可能的简单。所以,在某个阶段,我们也许应该依靠统计检验和置信区间。


 MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据
MATLAB奥运会奖牌预测研究 —CNN神经网络、逻辑回归、Liang-Kleeman信息流、多元回归及随机森林模型的因果关联与概率预测|附代码数据 Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据
Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据 【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用
【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用 Python预测二型糖尿病:逻辑回归、XGBoost、CNN、随机森林及BP神经网络融合加权线性回归细化变量及PCA降维创新
Python预测二型糖尿病:逻辑回归、XGBoost、CNN、随机森林及BP神经网络融合加权线性回归细化变量及PCA降维创新



