弹性网络正则化同时应用 L1 范数和 L2 范数正则化来惩罚回归模型中的系数。

由Kaizong Ye，Liao Bao撰写

为了在 R 中应用弹性网络正则化。

在 LASSO回归中，我们为 alpha 参数设置一个 ‘1’ 值，并且在岭回归中，我们将 ‘0’ 值设置为其 alpha 参数。

弹性网络是一种使用 L1，L2范数作为先验正则项训练的线性回归模型.这种组合允许学习到一个只有少量参数是非零稀疏的模型，就像 Lasso一样，但是它仍然保持一些像Ridge的正则性质。我们可利用 l1_ratio 参数控制L1和L2的凸组合。弹性网络是一不断叠代的方法。

弹性网络最妙的地方是它永远可以产生有效解。由于它不会产生交叉的路径，所以产生的解都相当不错。举例来说，对一个随机产生的50个城市的推销员问题，弹性网络的解只有比德宾和威尔萧的论文中所提的最具竞争力的演算法长2%（什么是最具竞争力的演算法？有人说是林－克尼根（Lin-Kernighan）演算法，也有人说是SA+OP）。但是弹性网络最吸引人的地方不在它的有效解，而在它收敛的速度。许多人试着去改善弹性网络收敛的速度，都有不错的结果。举例来说，柏尔（Burr）所提出的改良版可令50个城市的推销员问题的收敛次数由1250大幅降为30次。一个最佳化的弹性网络的速度会比林－克尼根快两倍。

弹性网络在很多特征互相联系的情况下是非常有用的。Lasso 很可能只随机考虑这些特征中的一个，而弹性网络更倾向于选择两个。在实践中，Lasso 和 Ridge 之间权衡的一个优势是它允许在循环过程（Under rotate）中继承 Ridge 的稳定性。

弹性网络在 0 到 1 的范围内搜索最佳 alpha 参数。在这篇文章中，我们将学习如何在 R 中应用弹性网络正则化。

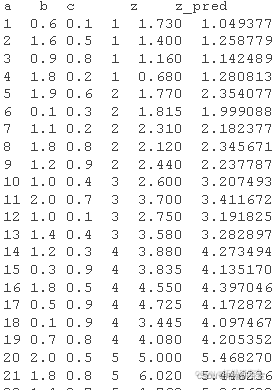
首先，我们将为本教程创建测试数据集。

df <- data.frame(a,b,c,z)
 
x <- as.matrix(df)\[,-4\]

for (i in 1:length(alpha))  {    bst$mse <- c(bet$mse, min(cg$cm)) }   inx <- which(bst$mse==min(bst$mse)) betlha <- bs$a\[inex\] be_mse <- bst$mse\[inex\]

接下来，我们再次使用最佳 alpha 进行交叉验证以获得 lambda（收缩水平）。

elacv <- cv(x, v)



bestbda <- elacv$lambda.min

视频

Lasso回归、岭回归等正则化回归数学原理及R语言实例

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

现在，我们可以使用函数拟合具有最佳 alpha 和 lambda 值的模型。

coef(elamod)

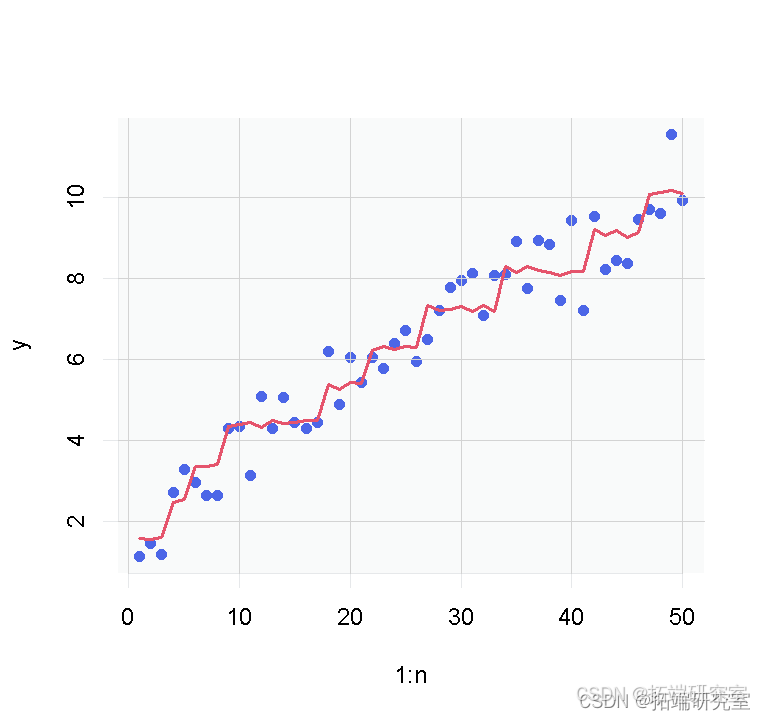
最后，我们可以使用模型预测测试数据并计算 RMSE、R 平方和 MSE 值。

predict(elasod, x)


cat(" RMSE:", rmse, "\\n", "R-squared:", R2, "\\n", "MSE:", mse)

R语言用加性多元线性回归、随机森林、弹性网络模型预测鲍鱼年龄和可视化

阅读文章 ➜

随时关注您喜欢的主题

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！