在对诊断测试准确性的系统评价中，统计分析部分旨在估计测试的平均（跨研究）敏感性和特异性及其变异性以及其他测量。
灵敏度和特异性之间往往存在负相关，这表明需要相关数据模型。
可下载资源
由于用户，分析在统计上具有挑战性
- 处理两个摘要统计，
- 必须考虑敏感性和特异性之间的相关性，
- 必须考虑到研究中的敏感性和特异性的异质性
- 应该允许纳入协变量。
1.文献检索（如何尽可能保证检索出所有相关文献的同时缩小检索文献的数目，一般需要检索pubmed,embase,如果是RCT需要检索cochrane library）
2.文献筛选（根据文献纳入排除标准筛选出合适文献筛选出）
3.数据提取（提取出需要合并的数据）
4.质量评价（利用量表对文献质量进行讨论）
5.异质性检验（检验各项研究是不是同质）
6.数据合并（利用软件对数据进行合并）
7.对结果的解释（关键）。
一篇好的meta分析的关键，不在于数据合并，而在于能够有效的文献检索，纳入高质量的文献，能够对异质性进行合理评价，对结果进行正确的解释。实验的成功与否在于设计，meta分析的成功与否也在于设计。初学者往往沉醉于学习各种meta分析数据合并的方法，而meta分析关键在于你对专业知识的理解。
本教程介绍并演示了用于诊断准确性研究的荟萃分析的分层混合模型。在层次结构的第一级中，给定每个研究的灵敏度和特异性，两个二项分布用于分别描述患病和健康个体中真阳性和真阳性样本数的变化。在第二级，我们使用二元分布模拟未观察到的敏感性和特异性。虽然使用了分层模型，但meta分析的重点在于研究中的汇总平均值，而在给定的研究估算中很少。
使用来自两个先前发布的meta分析的数据集来演示这些方法：
- 尿液中端粒酶的诊断准确性作为诊断原发性膀胱癌的肿瘤标志物，因为它是一个有问题的数据集，其相关参数估计为-1并且没有协变量而引起收敛问题（Glas et al.2003）
- 比较病毒检测（使用HC2检测）的敏感性和特异性与重复细胞学检查对具有宫颈病变的女性进行分类，以检测潜在的宫颈癌前病变（Arbyn等，2013）。第二个数据集用于证明具有一个协变量的元回归，该协变量可以自然地扩展到包括几个协变量。
荟萃Meta 分析的统计方法
推理框架和软件
由于其灵活性和MCMC模拟的使用，复杂建模通常可以在贝叶斯框架内更容易地实现。通过控制先验分布，贝叶斯推断可以规避可识别性问题，而没有先验分布的频率推理中的数值逼近算法可能会因识别性问题而陷入困境。然而，贝叶斯方法通常需要统计专业知识和耐心，因为MCMC模拟是计算密集型的。相反，最频繁的方法已被包含在标准“程序”中，这些程序需要较少的统计知识和编程技能。此外，频率论方法通过最大似然估计（MLE）进行优化，与MCMC模拟相比，其具有更短的运行时间。
JAGS （Plummer等人2003）是Stan的另一种可扩展的通用采样引擎。扩展JAGS需要知道C++动态链接库（DLL）模块。根据经验，配置和构建模块是一项艰巨而繁琐的任务，尤其是在Windows操作系统中。上述缺点加上这样的事实，Stan即使从较差的初始值开始，往往会以较少的迭代收敛。
模型诊断
为了评估链的模型收敛和平稳性，有必要检查潜在的比例缩减因子，有效样本大小（ESS），MCMC误差和参数的跟踪图。当所有链达到目标后验分布时，估计后验方差接近于链方差，使得两者的比率接近1，表明链是稳定，可能已达到目标分布。有效的样本大小表示实际上有关某个参数的信息量。当样本自动相关时，期望参数后验分布的信息少于样本独立时的信息。由于模拟了后验分布，因此近似值有可能偏离一定量;MCMC误差接近0表示可能已达到目标分布。
模型比较和选择
Watanabe-Alkaike信息准则（WAIC）（Watanabe 2010）是一种最近的模型比较工具，用于测量拟合模型在贝叶斯框架中的预测精度，用于比较模型。WAIC可以被视为对Deviance Information Criterion（DIC）的改进，尽管流行，但它已经存在一些问题（Plummer 2008）。WAIC是一个完全贝叶斯工具，非常接近贝叶斯交叉验证，对重新参数化不变，可用于简单以及分层和混合模型。
数据集
端粒酶数据
（Glas等，2003）系统地回顾了细胞学和其他标志物（包括端粒酶）对膀胱癌初步诊断的敏感性和特异性。他们报告说，端粒酶有敏感性和特异性分别为0.75 ，和0.86。他们得出结论，端粒酶不够灵敏，不宜用于日常使用。
将数据加载到R环境中并生成以下输出## ID TP TN FN FP
## 1 1 25 25 8 1
## 2 2 17 11 4 3
## 3 3 88 31 16 16
## 4 4 16 80 10 3
## 5 5 40 137 17 1
## 6 6 38 24 9 6
## 7 7 23 12 19 0
## 8 8 27 18 6 2
## 9 9 14 29 3 3
## 10 10 37 7 7 22ID是研究的标识符，DIS是患病的数量，TP是真阳性NonDis的数量，是健康TN的数量，是真阴性的数量。
ASCUS分类数据
（Arbyn等人，2013年）对人乳头瘤病毒检测的准确性进行了Cochrane评价，并重复细胞学分析，对宫颈涂片进行检查以诊断宫颈癌前病变。他们SAS使用BRMA模型进行METADAS了10项研究，其中使用了两种测试。他们用于HC2和重复细胞学的绝对灵敏度分别为0.909 [0.857, 0.944]和0.715 [0.629, 0.788]。这些数据用于演示如何在回归设置中扩展截距模型。将数据加载到R环境中并生成以下输出
## Test StudyID TP FP TN FN
## 1 RepC Andersson 2005 6 14 28 4
## 2 RepC Bergeron 2000 8 28 71 4
## 3 RepC Del Mistro 2010 20 191 483 7
## 4 RepC Kulasingam 2002 20 74 170 6
## 5 RepC Lytwyn 2000 4 20 26 2
## 6 RepC Manos 1999 48 324 570 15
## 7 RepC Monsonego 2008 10 18 168 15
## 8 RepC Morin 2001 14 126 214 5
## 9 RepC Silverloo 2009 24 43 105 10
## 10 RepC Solomon 2001 227 1132 914 40
## 11 HC2 Andersson 2005 6 17 25 4
## 12 HC2 Bergeron 2000 10 38 61 2
## 13 HC2 Del Mistro 2010 27 154 566 2
## 14 HC2 Kulasingam 2002 23 115 129 3
## 15 HC2 Lytwyn 2000 4 19 33 1
## 16 HC2 Manos 1999 58 326 582 7
## 17 HC2 Monsonego 2008 22 110 72 2
## 18 HC2 Morin 2001 17 88 253 2
## 19 HC2 Silverloo 2009 34 65 81 2
## 20 HC2 Solomon 2001 256 1050 984 11
Test是一个解释变量，显示分类测试的类型，StudyID是研究标识符，TP是真阳性数量，TN是真阴性的数量，FN是假阴性的数量。
截距模型
默认情况下，chains = 3 cores = 3。从上面的代码中，从每个3链中抽取1000样本，丢弃第一个样本，然后使得每个链具有900个“预烧期”后抽取。种子值seed = 3指定随机数生成器以允许结果的再现性，cores = 3允许通过使用3核来并行处理链，每个链一个核。
下面的迹线图显示了链和收敛。
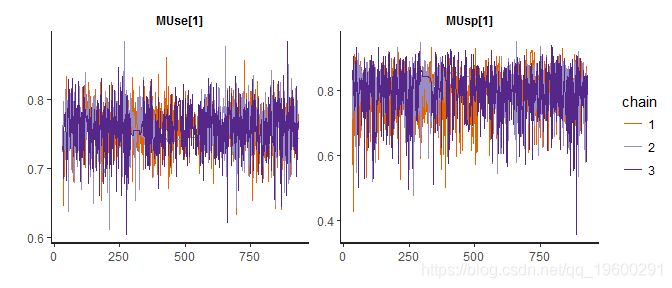
接下来，获得如下的模型概要估计
## Posterior marginal mean and median sensitivity and specificity
## with 95% credible intervals
##
## Parameter Mean Lower Median Upper n_eff Rhat
## MUse[1] Sensitivity 0.756762 6.904e-01 0.756036 0.81658 1196.9 1.001
## MUsp[1] Specificity 0.798289 6.171e-01 0.813517 0.90640 704.4 1.004
## ktau[1] Correlation -0.820176 -9.861e-01 -0.876343 -0.33334 269.2 1.015
## Varse[1] Var(Sens) 0.006198 8.321e-06 0.005047 0.01947 165.7 1.007
## Varsp[1] Var(Spec) 0.048111 1.357e-02 0.041060 0.12204 169.5 1.007
##
##
## Model characteristics
##
## Copula function: gauss, sampling algorithm: NUTS(diag_e)
##
## Formula(1): MUse ~ 1
## Formula(2): MUsp ~ 1
## Formula(3): Omega ~ 1
## 3 chain(s)each with iter=28000; warm-up=1000; thin=30.
## post-warmup draws per chain=900;total post-warmup draws=2700.
##
## Predictive accuracy of the model
##
## Log point-wise predictive density (LPPD): -38.0607
## Effective number of parameters: 7.5807
## Watanabe-Akaike information Criterion (WAIC): 91.2828## 95%置信区间的后验边缘平均值和中位数敏感性和特异性
## Parameter Mean Lower Median Upper n_eff Rhat
## MUse[1] Sensitivity 0.756762 6.904e-01 0.756036 0.81658 1196.9 1.001
## MUsp[1] Specificity 0.798289 6.171e-01 0.813517 0.90640 704.4 1.004
## ktau[1] Correlation -0.820176 -9.861e-01 -0.876343 -0.33334 269.2 1.015
## Varse[1] Var(Sens) 0.006198 8.321e-06 0.005047 0.01947 165.7 1.007
## Varsp[1] Var(Spec) 0.048111 1.357e-02 0.041060 0.12204 169.5 1.007
##
##
## 模型特征
##
## Copula function: gauss, sampling algorithm: NUTS(diag_e)
##
## Formula(1): MUse ~ 1
## Formula(2): MUsp ~ 1
## Formula(3): Omega ~ 1
## 3 chain(s)each with iter=28000; warm-up=1000; thin=30.
## post-warmup draws per chain=900;total post-warmup draws=2700.
#### 模型的预测准确性
##
## Log point-wise predictive density (LPPD): -38.0607
## Effective number of parameters: 7.5807
## Watanabe-Akaike information Criterion (WAIC): 91.2828## Posterior marginal mean and median sensitivity and specificity
## with 95% credible intervals
##
## Parameter Mean Lower Median Upper n_eff Rhat
## MUse[1] Sensitivity 0.756762 6.904e-01 0.756036 0.81658 1196.9 1.001
## MUsp[1] Specificity 0.798289 6.171e-01 0.813517 0.90640 704.4 1.004
## ktau[1] Correlation -0.820176 -9.861e-01 -0.876343 -0.33334 269.2 1.015
## Varse[1] Var(Sens) 0.006198 8.321e-06 0.005047 0.01947 165.7 1.007
## Varsp[1] Var(Spec) 0.048111 1.357e-02 0.041060 0.12204 169.5 1.007
##
##
## Model characteristics
##
## Copula function: gauss, sampling algorithm: NUTS(diag_e)
##
## Formula(1): MUse ~ 1
## Formula(2): MUsp ~ 1
## Formula(3): Omega ~ 1
## 3 chain(s)each with iter=28000; warm-up=1000; thin=30.
## post-warmup draws per chain=900;total post-warmup draws=2700.
##
## Predictive accuracy of the model
##
## Log point-wise predictive density (LPPD): -38.0607
## Effective number of parameters: 7.5807
## Watanabe-Akaike information Criterion (WAIC): 91.2828从上面的输出，所述元分析灵敏度MUse[1]和特异性MUsp[1]是0.7568 [0.6904, 0.8166]和0.7983 [0.6171, 0.9064]。灵敏度和特异性分别为0.0062 [0, 0.0195]和0.0048 [0.0136, 0.1220]。Kendall在敏感性和特异性之间的tau相关性估计为-0.8202 [-0.9861, -0.3333]。
以下命令生成一系列森林图。
## $G1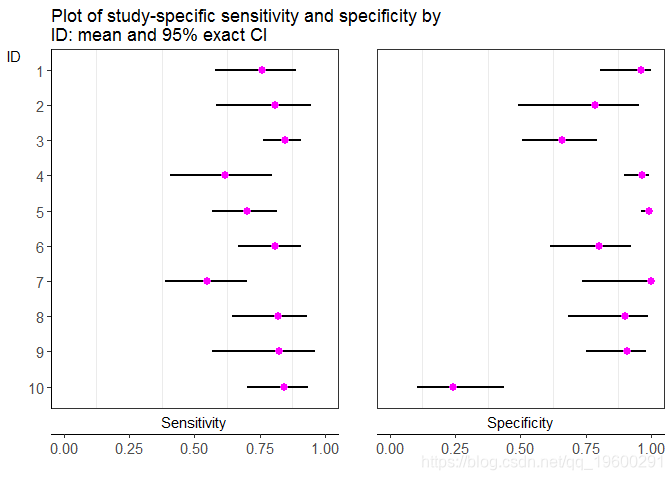
## ## $G2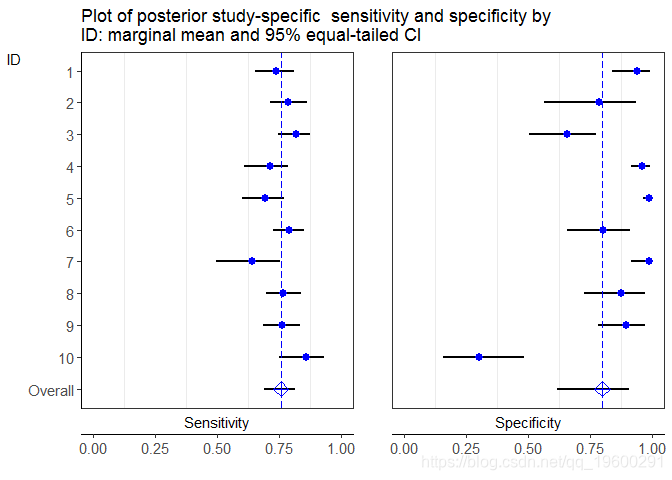
## ## $G3## Warning: Removed 2 rows containing missing values (geom_errorbar).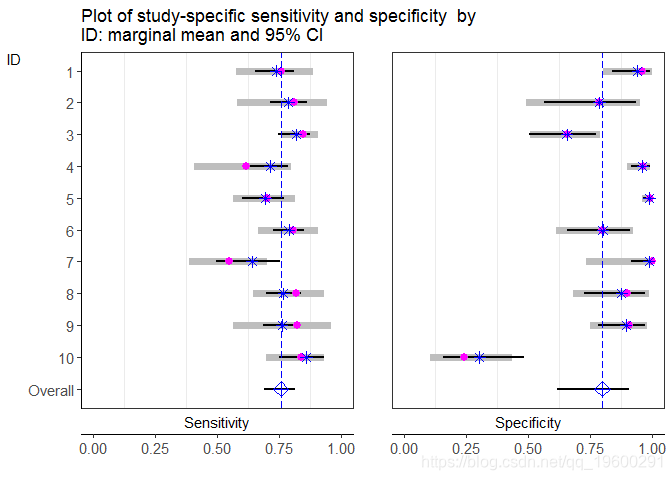
$G1是研究特异性敏感性和特异性（品红色点）及其相应的95％置信区间（黑线）的图。$G2是后验研究敏感性和特异性及其相应的95％置信区间（黑线）的图。
$G3是后验研究敏感性和特异性及其相应的95％置信区间（黑线）的图。还给出了研究特异性的灵敏度和特异性（品红点）及其相应的95％置信区间（粗灰线）。
如上图所示，总体平均敏感性和特异性存在“收缩”：后验研究的估计取决于全局估计，因此也取决于所有其他研究。
接下来，通过创建如下列表来准备数据
在data块中，指定了数据集中变量的维度和名称，此处Ns指数据集中的研究数量。该parameters块引入了待估计的未知参数。etarho; 表示Fisher氏变换的关联参数的形式的标量，mul表示的灵敏度和特异性在对数下的平均值为中心的观察值，其中随机效应是矢量零。
在transformed parameters块中进一步转换参数。在model块中定义所有参数和数据似然的先验分布。最后，在generated quantities块中，loglik是计算WAIC所需的对数似然向量。
接下来，stan调用函数将代码转换为C++，编译代码并从后验分布中提取样本，如下所示提取参数估计，并使用以下代码进一步检查链收敛和自相关
## Inference for Stan model: 61572683b29d52354783115614fab729.
## 3 chains, each with iter=5000; warmup=1000; thin=10;
## post-warmup draws per chain=400, total post-warmup draws=1200.
##
## mean se_mean sd 2.5% 50% 97.5% n_eff Rhat
## MU[1] 0.7525 0.0018 0.0517 0.6323 0.7562 0.8415 796 0.9999
## MU[2] 0.7908 0.0034 0.1095 0.5273 0.8094 0.9539 1045 1.0008
## mu[1] 0.7668 0.0013 0.0388 0.6869 0.7688 0.8369 891 0.9990
## mu[2] 0.8937 0.0027 0.0753 0.6943 0.9115 0.9825 789 0.9992
## rho -0.9311 0.0070 0.1353 -0.9996 -0.9813 -0.5626 372 1.0077
## Sigma[1,1] 0.3376 0.0091 0.2918 0.0579 0.2554 0.9851 1026 1.0023
## Sigma[1,2] -1.2291 0.0272 0.8765 -3.4195 -1.0031 -0.2724 1040 0.9991
## Sigma[2,1] -1.2291 0.0272 0.8765 -3.4195 -1.0031 -0.2724 1040 0.9991
## Sigma[2,2] 5.6827 0.1282 4.1931 1.4720 4.6330 16.9031 1070 1.0002
##
## Samples were drawn using NUTS(diag_e) at Mon Oct 09 09:19:55 2017.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).随时关注您喜欢的主题
所述元分析灵敏度（MU[1]）和特异性（MU[2]）和95％置信区间是0.7525[0.6323, 0.8415]和0.7908[0.5273, 0.9539]。这与作者以两种方式发表的文章（0.75 [0.66,0.74]和0.86 [0.71,0.94]）不同。作者将标准双变量正态分布拟合到logit转换的敏感性和特异性值，在研究中允许研究之间的异质性，并忽略了更高层次的分层模型。因此，作者必须使用0.5的连续性校正，这是分层模型中没有遇到的问题。
下图显示除了Clayton copula模型之外，大多数拟合模型的链条混合效果令人满意，几乎没有自相关。
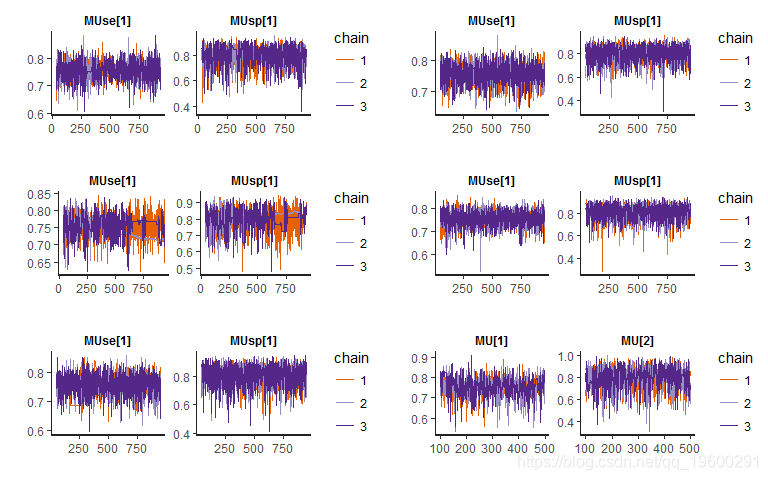
所有拟合分布估计的平均灵敏度和特异性如下表所示。
## Model Parameter Mean Lower Median Upper n_eff
## 1 Gaussian Sensitivity 0.756762 6.904e-01 0.756036 8.166e-01 1196.857
## 2 Gaussian Specificity 0.798289 6.171e-01 0.813517 9.064e-01 704.379
## 3 Gaussian Correlation -0.820176 -9.861e-01 -0.876343 -3.333e-01 269.179
## 4 Gaussian Var(Sens) 0.006198 8.321e-06 0.005047 1.947e-02 165.705
## 5 Gaussian Var(Spec) 0.048111 1.357e-02 0.041060 1.220e-01 169.508
## 6 C90 Sensitivity 0.751379 6.913e-01 0.753546 8.098e-01 25.638
## 7 C90 Specificity 0.807051 6.549e-01 0.821119 9.069e-01 119.897
## 8 C90 Correlation -0.528340 -9.766e-01 -0.725178 -4.020e-18 4.111
## 9 C90 Var(Sens) 0.004885 3.400e-04 0.003297 1.955e-02 11.615
## 10 C90 Var(Spec) 0.045694 1.556e-02 0.038049 1.020e-01 137.149
## 11 C270 Sensitivity 0.757528 6.877e-01 0.761163 8.210e-01 273.236
## 12 C270 Specificity 0.803502 6.328e-01 0.811740 9.097e-01 1081.987
## 13 C270 Correlation -0.697493 -9.827e-01 -0.808717 -3.332e-06 40.012
## 14 C270 Var(Sens) 0.006662 2.667e-04 0.005293 2.027e-02 556.055
## 15 C270 Var(Spec) 0.044767 1.268e-02 0.037922 1.112e-01 1098.815
## 16 FGM Sensitivity 0.759407 6.891e-01 0.761931 8.174e-01 2475.208
## 17 FGM Specificity 0.802588 6.453e-01 0.812498 9.045e-01 2293.332
## 18 FGM Correlation -0.174538 -2.222e-01 -0.222221 2.222e-01 785.016
## 19 FGM Var(Sens) 0.005390 7.425e-07 0.004181 1.813e-02 1019.633
## 20 FGM Var(Spec) 0.041890 1.177e-02 0.036671 9.997e-02 2479.371
## 21 Frank Sensitivity 0.756683 6.855e-01 0.758340 8.152e-01 2686.631
## 22 Frank Specificity 0.808239 6.472e-01 0.818777 9.110e-01 1910.561
## 23 Frank Correlation -0.706819 -8.550e-01 -0.692019 1.000e+00 2700.000
## 24 Frank Var(Sens) 0.006678 5.896e-04 0.005280 2.140e-02 2699.766
## 25 Frank Var(Spec) 0.042067 1.201e-02 0.035908 1.039e-01 1937.653
## 26 BRMA Sensitivity 0.752531 6.323e-01 0.756181 8.415e-01 796.037
## 27 BRMA Specificity 0.790796 5.273e-01 0.809420 9.539e-01 1044.902
## 28 BRMA Correlation -0.822353 -9.824e-01 -0.876654 -3.804e-01 238.268
## 29 BRMA Var(lSens) 0.337556 5.792e-02 0.255387 9.851e-01 1025.609
## 30 BRMA Var(lSpec) 5.682692 1.472e+00 4.632967 1.690e+01 1070.481
## Rhat WAIC
## 1 1.0014 91.28
## 2 1.0044 91.28
## 3 1.0154 91.28
## 4 1.0072 91.28
## 5 1.0069 91.28
## 6 1.1047 91.40
## 7 1.0304 91.40
## 8 1.3707 91.40
## 9 1.1005 91.40
## 10 1.0311 91.40
## 11 1.0096 90.75
## 12 1.0001 90.75
## 13 1.0407 90.75
## 14 1.0024 90.75
## 15 0.9999 90.75
## 16 0.9998 97.37
## 17 0.9996 97.37
## 18 1.0070 97.37
## 19 1.0034 97.37
## 20 0.9999 97.37
## 21 0.9994 90.55
## 22 0.9997 90.55
## 23 NaN 90.55
## 24 0.9990 90.55
## 25 0.9992 90.55
## 26 0.9999 86.76
## 27 1.0008 86.76
## 28 1.0218 86.76
## 29 1.0023 86.76
## 30 1.0002 86.76结果以图形方式呈现如下
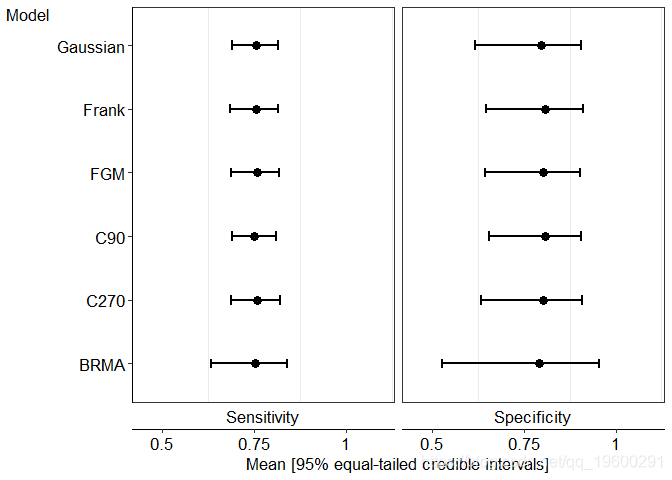
模型比较
上面显示，BRMA模型和高斯copula双变量β估计的相关性更加极端。另一个极端是模型FGM copula双变量β的估计，这是由于FGM copula中关联参数的约束，其中值在| 2/9 |内。
在上图中g1，尽管相关结构存在差异，但五个双变量β分布的边际平均灵敏度和特异性与95％置信区间的细微差异相当。
在没有估计困难的情况下，上表显示了Pearson估计的相关性-0.8224[-0.9824, -0.3804]。这是因为贝叶斯方法不受样本量的影响，因此能够处理具有较少问题的小样本量的情况。
基本上，所有六个模型在第一级层次结构中是等价的，并且在指定“研究特异性”敏感性和特异性的先验分布不同。因此，模型应具有相同数量的参数，在这种情况下，比较预测密度是有意义的。在检查时，来自五个基于copula的模型的对数预测密度实际上是等效的（min=-38.77, max=-37.89）但是参数的有效数量有点不同（min=7.25, max=9.92）。
Meta回归
ascus数据集有Test作为协变量。使用协变量是有意义的，以研究其对敏感性和特异性（包括相关性）的联合分布的影响。以下将基于copula的二元beta二项分布拟合到ascus数据。
下图显示了适用于ascus数据的所有六个模型的迹线图，其中所有参数（包括相关参数（BRMA除外））都被建模为协变量的函数。除了基于Clayton copula的双变量β的情况外，存在适当的链混合和收敛。
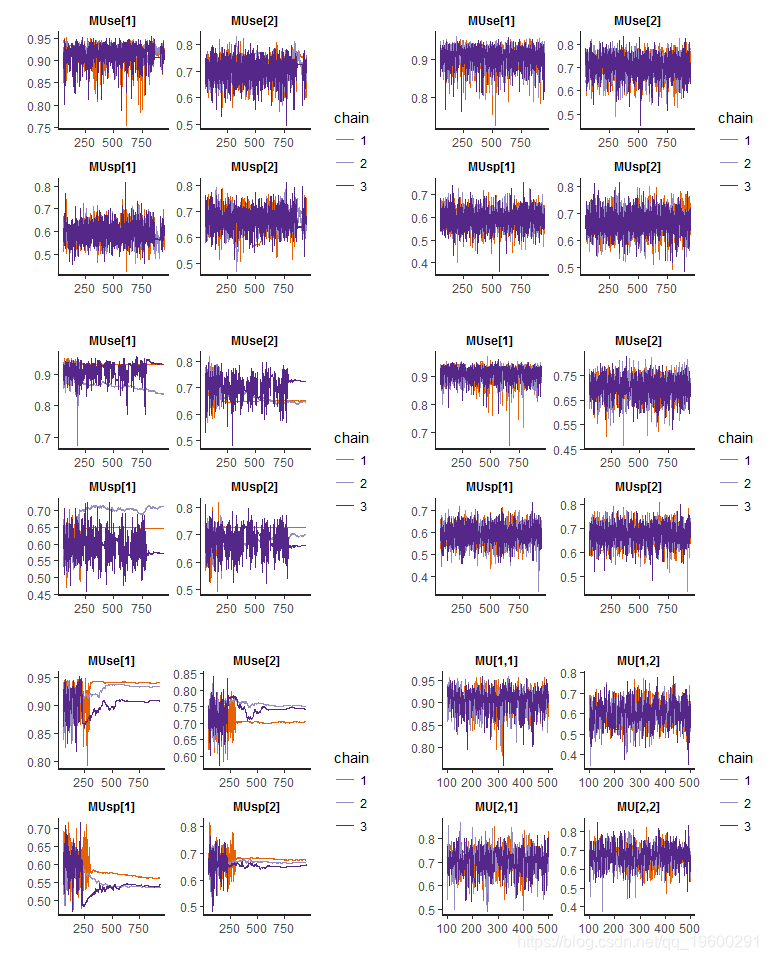
从基于copula的双变量β分布来看，很明显HC2和重复细胞学中的敏感性和特异性之间的相关性是不同的。
## Warning: 19 (47.5%) p_waic estimates greater than 0.4.
## We recommend trying loo() instead.## Model Test Parameter Mean Lower Median Upper
## 9 Gaussian HC2 Correlation -0.43812 -0.9984 -6.959e-01 9.847e-01
## 10 Gaussian Repc Correlation -0.91991 -0.9997 -9.643e-01 -6.103e-01
## 23 C90 HC2 Correlation -0.06588 -0.7610 -1.039e-17 -7.624e-19
## 24 C90 Repc Correlation -0.85157 -0.9804 -9.120e-01 -4.906e-01
## 37 C270 HC2 Correlation -0.03038 -0.6452 -7.000e-18 -1.782e-18
## 38 C270 Repc Correlation -0.77847 -0.9757 -7.058e-01 -5.394e-01
## 51 FGM HC2 Correlation -0.07618 -0.2222 -2.215e-01 2.222e-01
## 52 FGM Repc Correlation -0.19819 -0.2222 -2.222e-01 1.894e-01
## 65 Frank HC2 Correlation -0.48806 -0.8140 -4.497e-01 1.000e+00
## 66 Frank Repc Correlation -0.73784 -0.8627 -7.275e-01 1.000e+00
## 81 BRMA Both Correlation -0.84808 -0.9839 -8.980e-01 -4.497e-01
## n_eff Rhat WAIC
## 9 154.238 1.0066 236.4
## 10 24.342 1.0542 236.4
## 23 30.089 1.0690 235.7
## 24 8.532 1.1128 235.7
## 37 76.410 1.0326 227.5
## 38 2.945 1.4613 227.5
## 51 2422.935 1.0007 245.1
## 52 2550.145 0.9997 245.1
## 65 2700.000 NaN 238.3
## 66 2700.000 NaN 238.3
## 81 102.983 1.0254 233.7Clayton90模型具有最低的WAIC。
因此，这个例子表明，检查模型的拟合度和合理性是否充分是至关重要的，而不是盲目地依赖信息标准来选择最适合数据的标准。
从下面绘制的后验相对敏感性和特异性，所有收敛的模型通常认为重复细胞学比HC2敏感性低，而特异性没有显着损失。
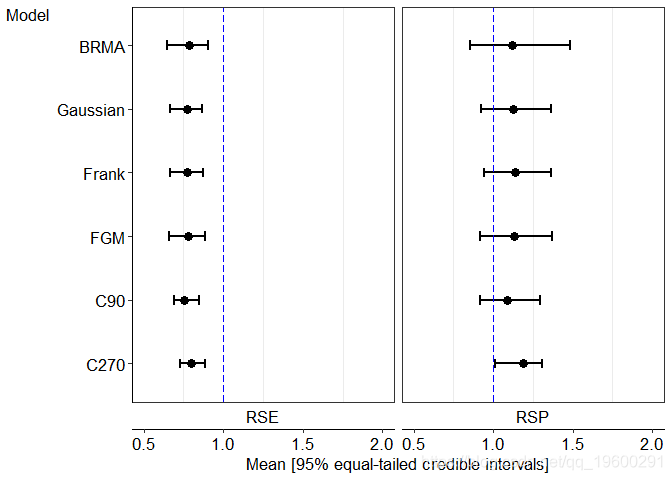
讨论
基于Copula的模型提供了极大的灵活性和易用性，但它们需要谨慎使用。虽然本文中使用的copula具有吸引力，因为它们在数学上易于处理，但（Mikosch 2006）和（Genest and Remillard 2006）指出，从数据中估算copula可能很困难。此外，copula模型背后的概念稍微复杂一些，因此需要统计专业知识来理解和编程，因为它们尚未作为统计软件中的标准程序。
在本文中，简要讨论了几种用于诊断准确性研究的metat统计模型。
在评估meta分析的敏感性和特异性以及相关性时，模型之间存在一些差异。因此，有必要进一步研究某些参数的影响，例如研究数量，样本量和联合分布的指定对meta分析的估计。
结论
提出的贝叶斯模型使用copula来构建二元β分布，该模型估计特定研究的敏感性和特异性，具有特定的随机效应值。
在ASCUS分类数据中，基于拟合模型的结论与作者得出的结论一致：HC2比重复细胞学检查更敏感但更轻微，并且没有明显低于特异性巴氏涂片诊断宫颈癌前病变的女性。
虽然BRMA对于两个数据集都具有最低的WAIC，但我们仍然建议使用双变量β分布对灵敏度和特异性进行建模，因为它们可以直接提供meta分析估计。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言贝叶斯分析：INLA 、MCMC混合模型、生存分析肿瘤临床试验、间歇泉喷发时间数据应用|附数据代码
R语言基于贝叶斯分层、层次Hierarchical Bayesian模型的房价数据空间分析
【视频讲解】Python贝叶斯卷积神经网络BCNN分类胸部X光图像数据集实例
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
