
和宏观经济数据不同,金融市场上多为高频数据,比如股票收益率序列。
直观的来说 ,后者是比前者“波动”更多且随机波动的序列,在一元或多元的情况下,构建Copula函数模型和GARCH模型是最好的选择。
可下载资源
多元GARCH家族中,种类非常多,需要自己多推导理解,选择最优模型。本文使用R软件对3家上市公司近十年的每周收益率为例建立模型。
首先我们可以绘制这三个时间序列。
经济全球化的发展致使各国之间愈加紧密的经济联动,如果某一国家的金融领域发生危机,危机将在各国金融市场间快速传播。为了降低金融危机的负面影响,人们愈加重视金融市场间关联性的研究。在准确把握市场关联性的基础上进行金融对冲,投资获利的同时有效降低商业风险。
研究金融资产相关性最重要的前提条件是确定资产收益率序列的拟合模型,即边缘拟合模型。Engle Robert 发明了ARCH模型(自回归条件异方差模型),但当模型残差序列的异方差函数具有长期自相关性时,ARCH模型的拟合精度会受到影响。为此Bollerslev [以ARCH模型为基础,提出了GARCH模型(广义自回归条件异方差模型),该模型很好地描述出市场波动的异方差性和波动集群性。
在动态研究金融变量间的相依关系领域,Copula-GARCH模型建立金融市场间的非线性相关关系,优点是边缘拟合GARCH模型残差择优服从t分布或GED分布,缺点是高维相关结构整体为Gaussian Copula函数。
Copula函数
Copula理论即可以将一个联合分布函数分解成多个边缘分布函数和一个Copula函数,适合描述多维随机变量相关关系的复杂性。
定理 :令 F 为一个 n 维随机向量的联合分布函数,其中各变量的边缘分布函数记为 Fi ,那么一定存在一个Copula函数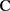 ,使得 ,其中 Fi(xi)∈(0,1),i=1,⋯,n 。若边缘分布函数 Fi 是连续的一元函数,则Copula函数 C 的形式是唯一确定的。
,使得 ,其中 Fi(xi)∈(0,1),i=1,⋯,n 。若边缘分布函数 Fi 是连续的一元函数,则Copula函数 C 的形式是唯一确定的。
Copula理论发展出了各种形式的家族函数,经常使用的类型主要分为两类:一类是椭球Copula,常用的包括Gaussian Copula和t-Copula;另外一类是由生成函数 φ(t) ( t 为边缘分布)生成的阿基米德Copula,包括Clayton Copula、Gumbel Copula和Frank Copula。其中以边缘分布函数( u,v )为自变量的二元Gaussian Copula、t-Copula、Clayton Copula、Gumbel Copula、Frank Copula分布函数具体的表达式分别如式(1)~(5)所示。
C1(u,v;ρ)=∫Φ−1(u)−∞∫Φ−1(v)−∞12π√1−ρ2exp(−(s2+r2−2ρsr)2(1−ρ2)) dsdr(1)
式中: Φ−1(•) 为标准正态分布函数 Φ(•) 的逆函数;相关系数 ρ∈(−1,1) ; s,r 分别为 的自变量。
C2(u,v;ρ,m)=∫T−1m(u)−∞∫T−1m(v)−∞12π√1−ρ2exp[1+−(s2+r2−2ρsr)m(1−ρ2)]−m+22dsdr(2)
式中: T−1m(•) 为自由度是 的一元t分布函数 Tm(•) 的逆函数;相关系数 ; 分别为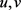 的自变量。
的自变量。
C3(u,v;θ)=(u−θ+v−θ−1)−1θ(3)
式中:生成函数 φ(t)=t−θ−1θ,θ∈(−1,∞)\{0} 。
C4(u,v;θ)=exp(−[(−lnu)1θ+(−lnv)1θ]θ)(4)
式中:生成函数 。
C5(u,v;θ)=−1θln(1+(e−θu−1)(e−θv−1)e−θ−1)(5)
式中:生成函数 φ(t)=−lne−θt−1e−θ−1,θ≠0 。
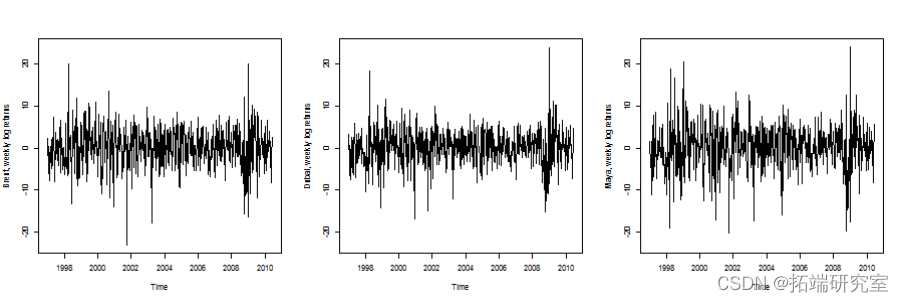
在这里使用多变量的ARMA-GARCH模型。
本文考虑了两种模型
1 ARMA模型残差的多变量GARCH过程
2 ARMA-GARCH过程残差的多变量模型(基于Copula)
ARMA-GARCH模型
> fit1 = garchFit(formula = ~arma(2,1)+ garch(1,1),data = dat [,1],cond.dist =“std”)可视化波动
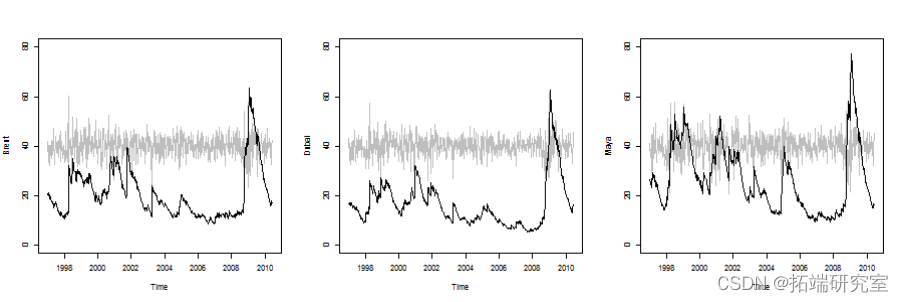
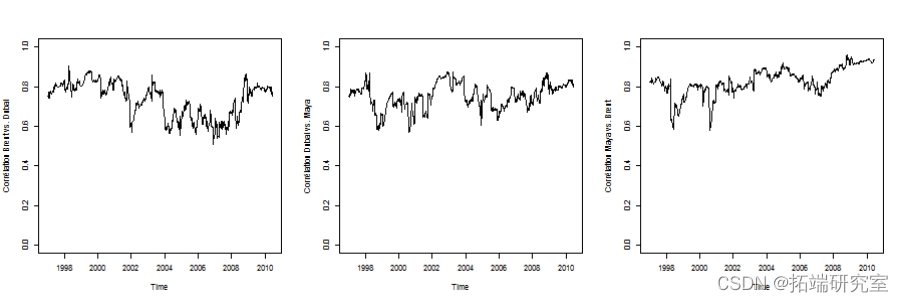
隐含的相关性
> emwa_series_cor = function(i = 1,j = 2){
+ if((min(i,j)== 1)&(max(i,j)== 2)){+ a = 1; B = 5; AB = 2}
+}
BEKK(1,1)模型:
BEKK11(dat_arma)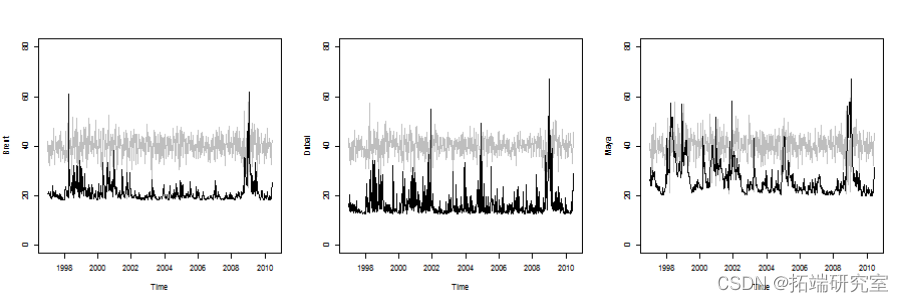
隐含的相关性
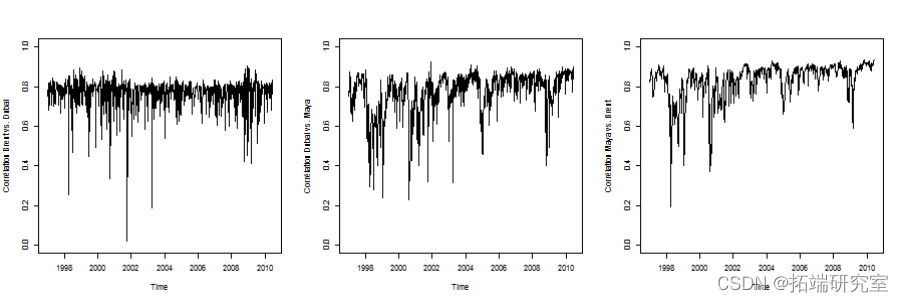
对单变量GARCH模型残差建模
对单变量GARCH模型残差建模
第一步可能是考虑残差的静态(联合)分布。单变量边际分布是
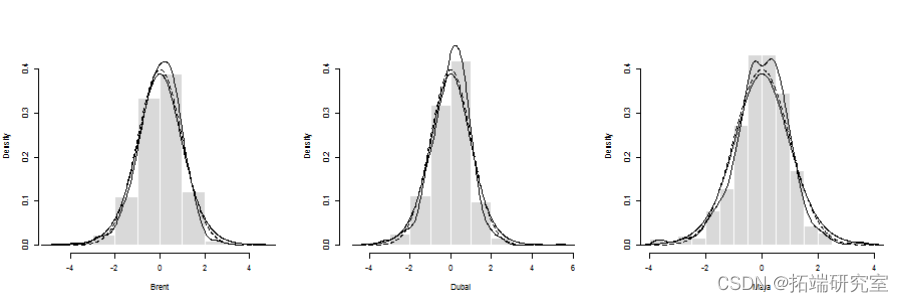
而联合密度为
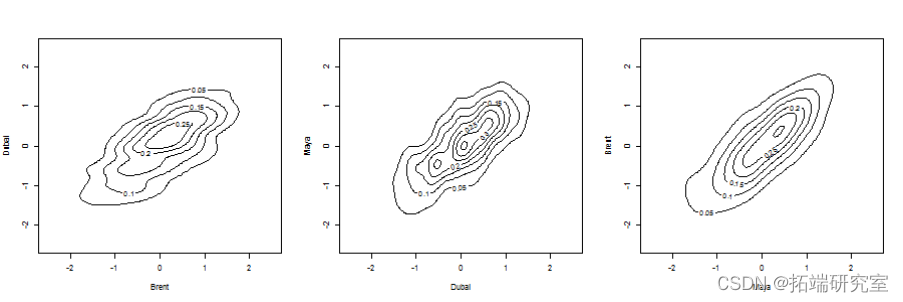
可视化密度
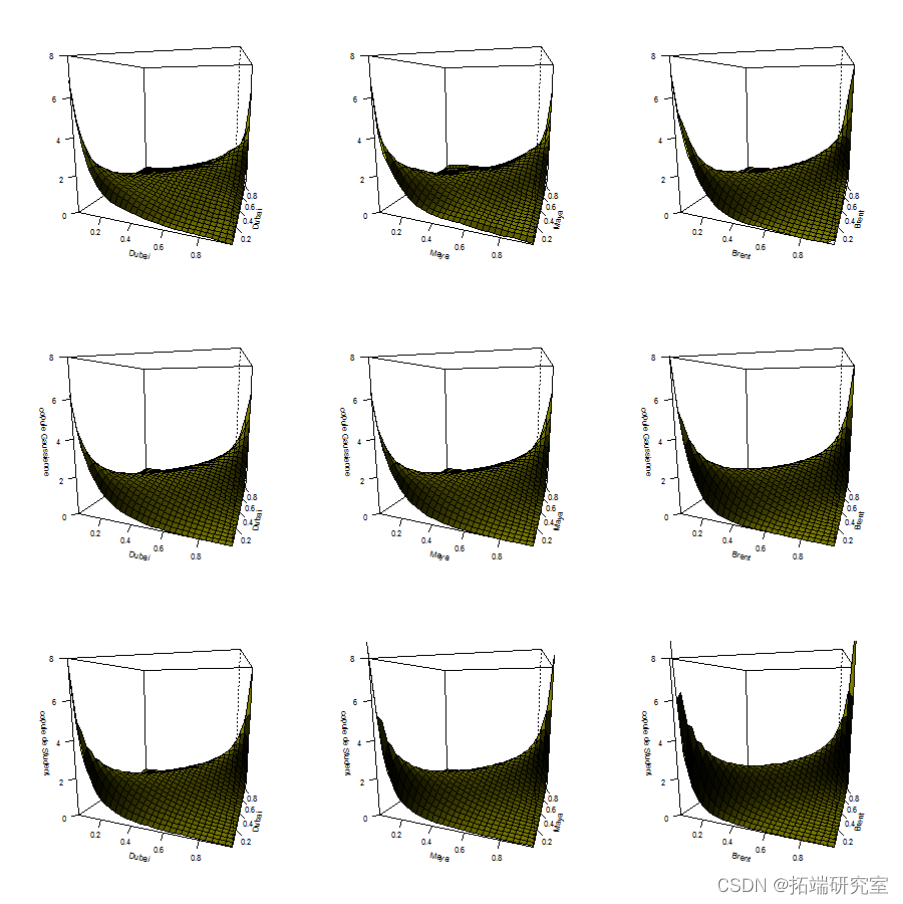
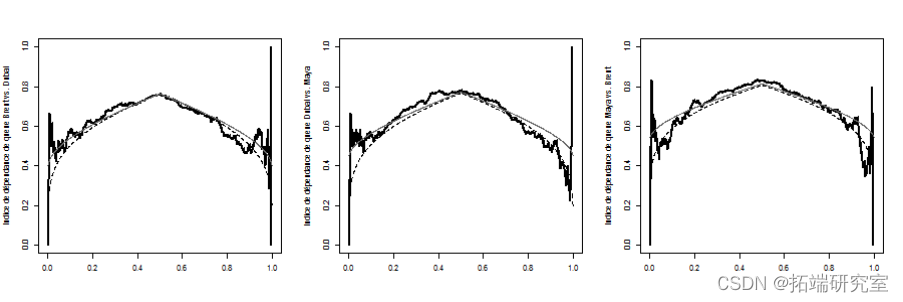
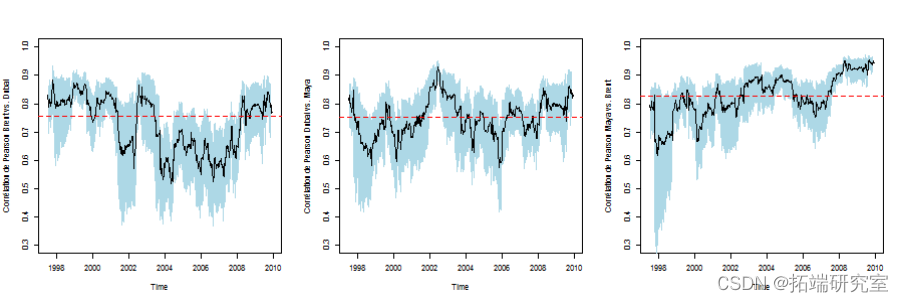
查看相关性是否随着时间的推移而稳定。
斯皮尔曼相关性
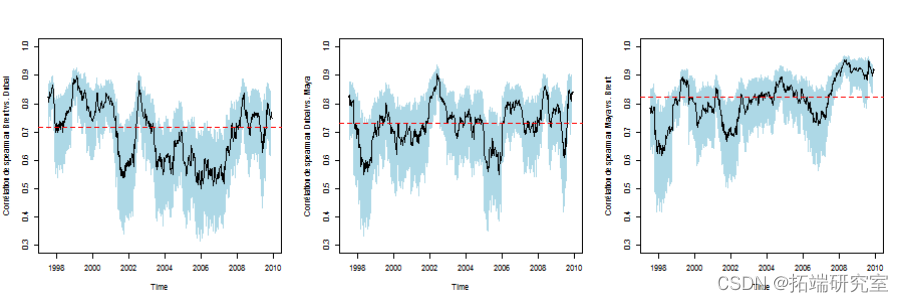
肯德尔相关性
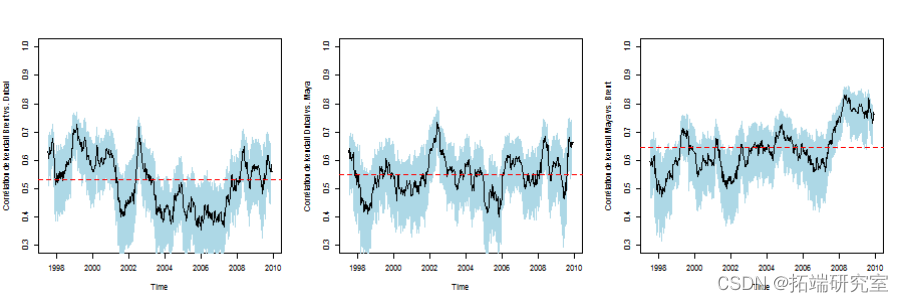
随时关注您喜欢的主题
对相关性建模,考虑DCC模型
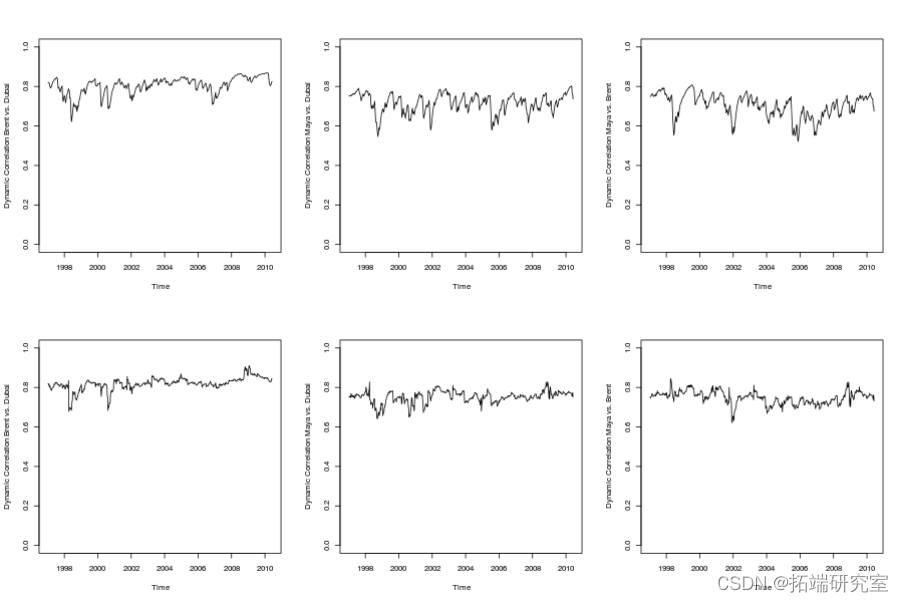
对数据进行预测
> fcst = dccforecast(dcc.fit,n.ahead = 200)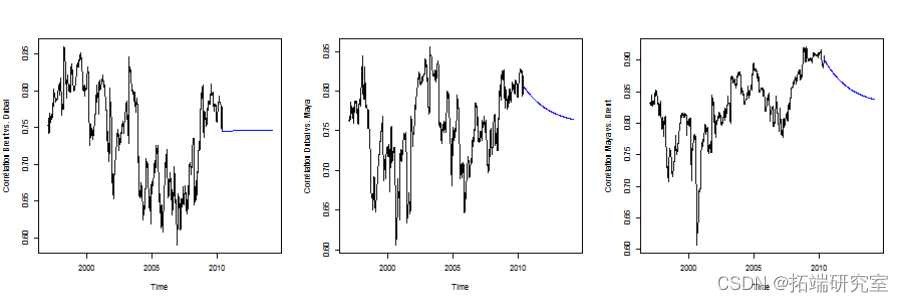
我们已经完全掌握了多元GARCH模型的使用,接下来就可以放手去用R处理时间序列了!


 Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据
Python实现Transformer神经网络时间序列模型可视化分析商超蔬菜销售数据筛选高销量单品预测|附代码数据 Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据
Python梯度提升树GBT、随机森林、决策树对链家多城市二手房价格数据预测与区域差异可视化分析——基于数据爬取与特征工程优化|附代码数据 Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究
Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究 Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证
Python农业气象预测:优化决策树、SHAP模型可解释性、滑动窗口时序分析及交叉验证



