作为先决条件,我们将使用几行代码
在代码中,我们创建了一些测试数据,其中因变量 y 线性依赖于自变量 x(预测变量)
定义线性模型拟合数据的可能性和先验
我们理解一下为什么拒绝抽样是可行的,这对我们之后运用随机模拟思想非常关键!
该简单分布与高斯分布的趋势大致相同,中间大两头小,因此取到中间的z zz的概率比较大;
通过u 0
进一步筛选z ,p ( z ) 较低时拒绝率较大,反之接受率较高,大致符合p ( z ) 分布要求。
一句话,通过简单抽样和设置接受率,“强迫”结果趋于复杂分布。
这样,我们就通过简单的高斯分布采样,以及计算机可直接实现的均匀采样,间接实现了复杂的p ( z ) p(z)p(z)采样。
然而,在高维情况下,该方法的劣势很明显:
合适的简单分布q ( z ) q(z)q(z)很难找到。
合适的k kk值很难找到。
这两个问题会导致拒绝率极高,计算效率很低。其根本缺陷在于:样本之间是独立无关的。
并实现一个简单的 Metropolis-Hastings MCMC 从该模型的后验分布中采样。
x = (-(sleze-1)/2):((sple-1)/2) y = treA * x + tuB + rnorm(n=sapeize,mean=0,sd=tuSd)
所以,让我们运行 MCMC:
stavalue = c(4,2,8) cn = rmtrisMCC(avae, 10000)
由 coda 促成的链的一些简单总结
好吧,coda 是一个 R 包,它提供了许多用于绘制和分析后验样本的标准函数。为了使这些功能起作用,您需要将输出作为“mcmc”或“mcmc.list”类的对象,我们将在后面讨论。
可下载资源
拥有一个 coda 对象的好处是我们通常想要用链做的很多事情都已经实现了,所以例如我们可以简单地 summary() 和 plot() 输出
summary(chn) plot(cn)
视频
R语言中RStan贝叶斯层次模型分析示例
视频
贝叶斯推断线性回归与R语言预测工人工资数据
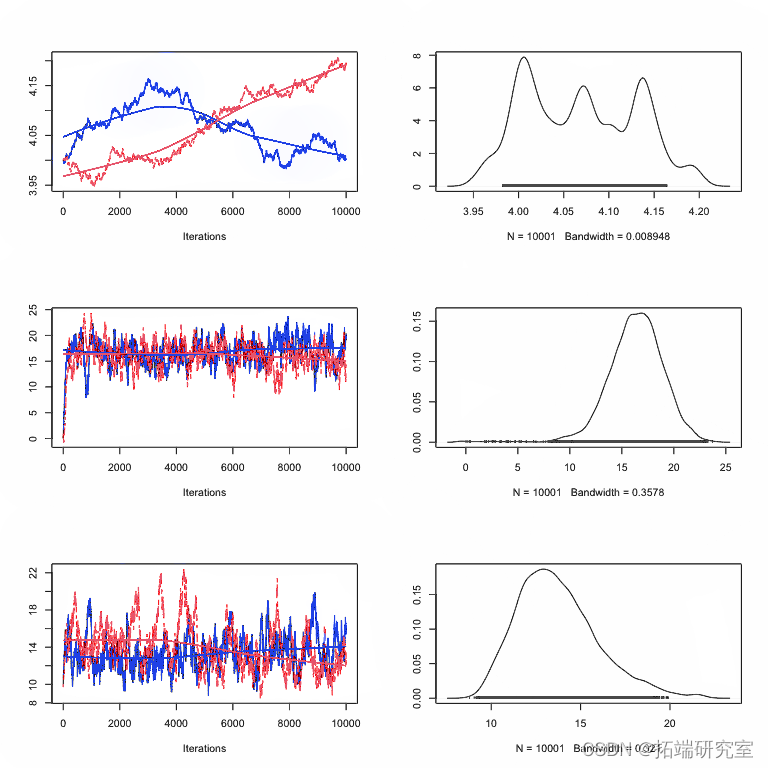
它提供了一些关于控制台的有用信息和一个大致如下所示的图:
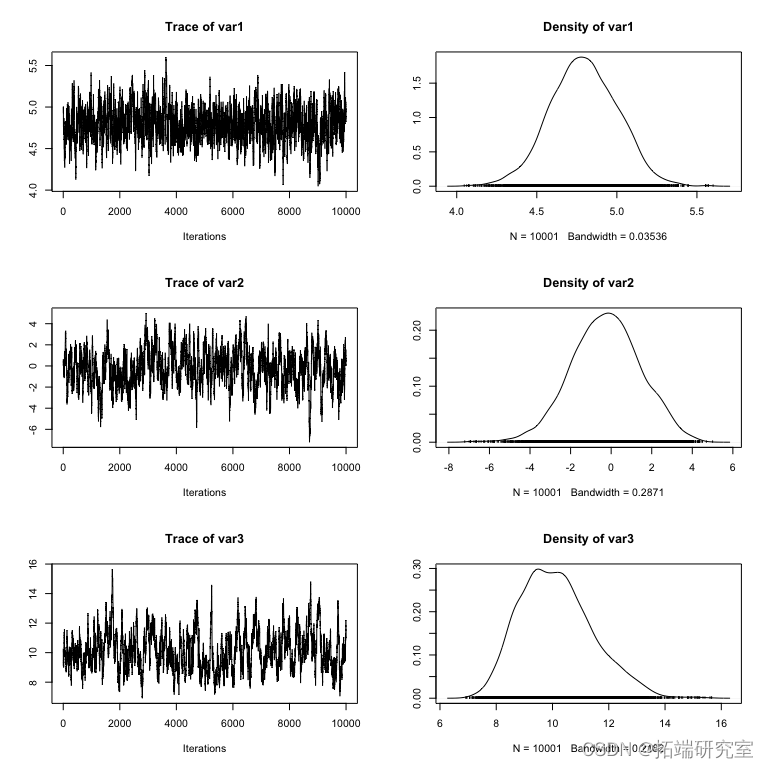
图: 一个 coda 对象的 plot() 函数的结果
plot() 函数的结果:每一行对应一个参数,因此每个参数有两个图。左边的图称为轨迹图——它显示了参数在链运行时所取的值。右图通常称为边际密度图。基本上,它是轨迹图中值的(平滑的)直方图,即参数值在链中的分布。
边际密度隐藏了相关性
边际密度是参数取值与所有其他“边缘化”参数的平均值,即其他参数根据其后验概率具有任何值。通常,边际密度被视为贝叶斯分析的主要输出(例如,通过报告它们的均值和标准差),但我强烈建议不要进一步分析这种做法。原因是边际密度“隐藏”了参数之间的相关性,如果存在相关性,参数的不确定性在边际中似乎要大得多。
随时关注您喜欢的主题
Plot(data.frame(can))
在我们的例子中,应该没有大的相关性,因为我以这种方式设置了示例
x = (-(samee-1)/2):((smeie-1)/2) + 20
再次运行 MCMC 并检查相关性应该会给你一个完全不同的画面。
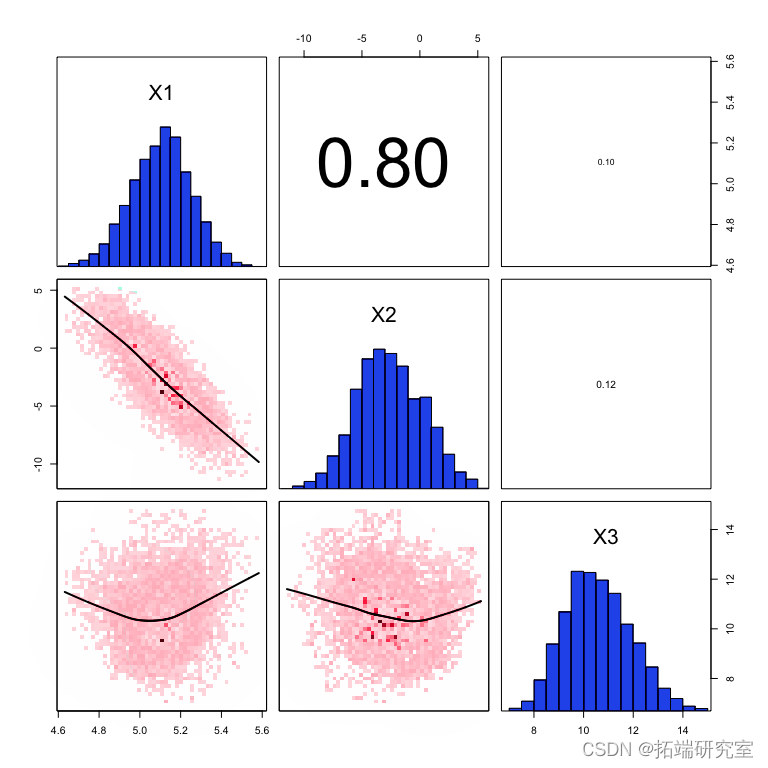
图: 不平衡 x 值拟合的边际密度(对角线)、配对密度(下图)和相关系数(上图)
您可以看到第一个和第二个参数(斜率和截距)之间的强相关性,并且您还可以看到每个参数 X2 的边际不确定性增加了。
请注意,我们在这里只检查了配对相关性,可能仍然有更高阶的交互不会出现在这样的分析中,所以你可能仍然遗漏了一些东西。
收敛诊断
现在,到收敛:一个 MCMC 从后验分布创建一个样本,我们通常想知道这个样本是否足够接近后验以用于分析。有几种标准方法可以检查这一点,但我建议使用 Gelman-Rubin 诊断。
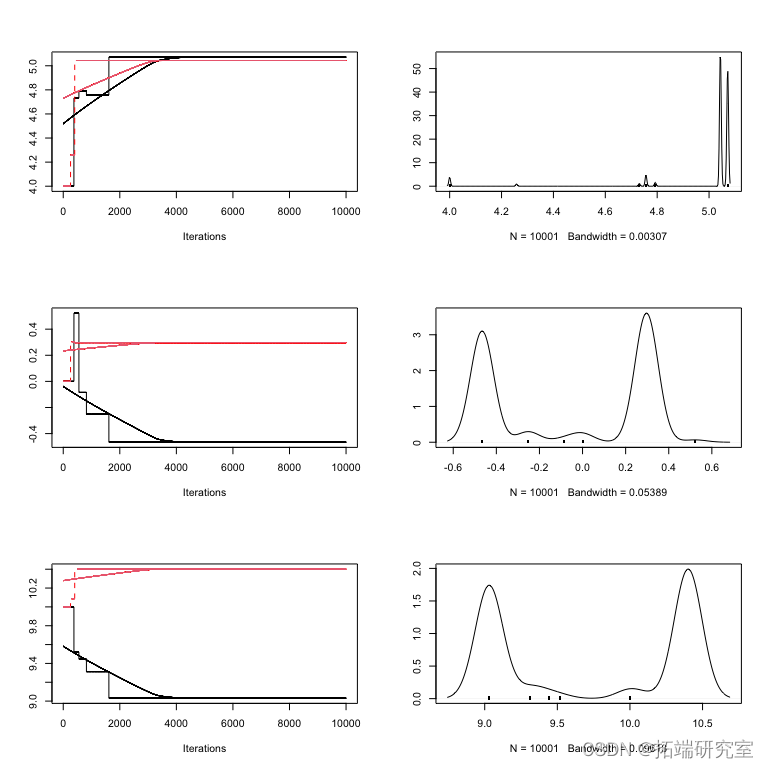
结果图应该是这样的
cha2 = runmeooi_MCMC(arvue, 10000) cominchns = mcmc.list(cai, ain2) plot(coinchns)
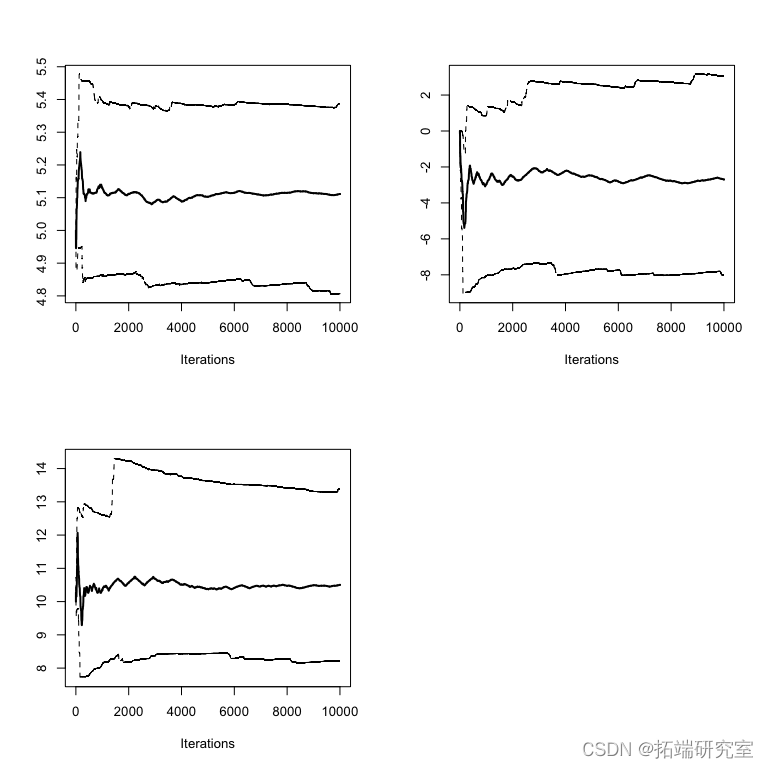
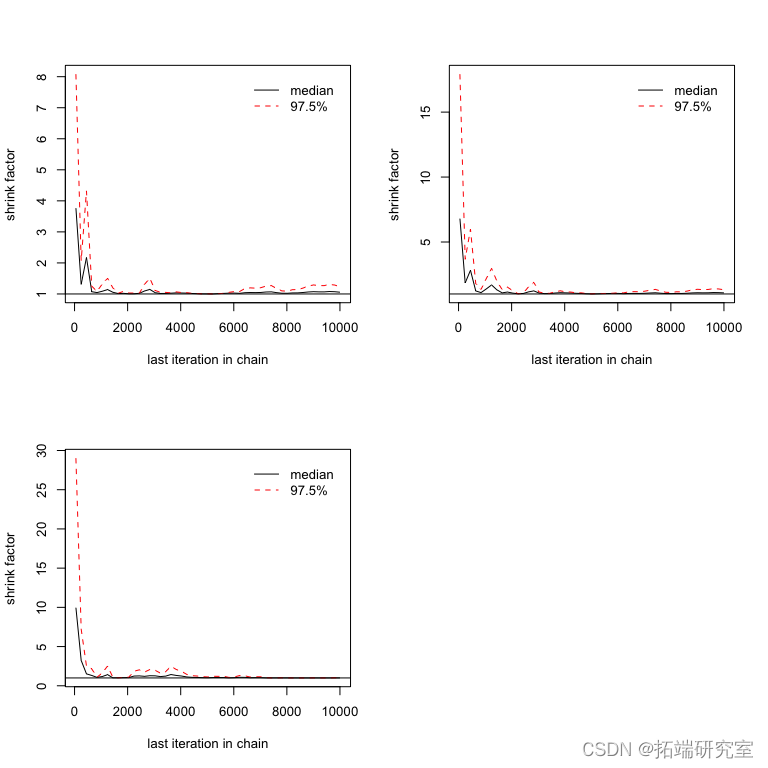
图: 结果
diag 为您提供每个参数的比例缩减因子。因子 1 意味着方差和链内方差相等,较大的值意味着链之间仍然存在显着差异。
改善收敛/混合
那么,如果还没有收敛怎么办?当然,你总是可以让 MCMC 运行更长时间,但另一个选择是让它收敛得更快。可能会发生两件事:
- 与我们从中抽样的分布相比,您的提议函数很窄——接受率高,但我们没有得到任何结果,混合不好
- 与我们从中抽样的分布相比,您的提议函数太宽了——接受率低,大部分时间我们都呆在原地
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据 【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用
【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用 Python电影票房预测模型研究——贝叶斯岭回归Ridge、决策树、Adaboost、KNN分析猫眼豆瓣数据
Python电影票房预测模型研究——贝叶斯岭回归Ridge、决策树、Adaboost、KNN分析猫眼豆瓣数据 Python员工数据人力流失预测:ADASYN采样CatBoost算法、LASSO特征选择与动态不平衡处理及多模型对比研究
Python员工数据人力流失预测:ADASYN采样CatBoost算法、LASSO特征选择与动态不平衡处理及多模型对比研究



