此示例显示如何 lasso 识别和舍弃不必要的预测变量。
我们围绕Lasso技术进行一些咨询，帮助客户解决独特的业务问题。使用各种方法从指数分布生成 200 个五维数据 X 样本。
rng(3,'twister') % 实现可重复性 for i = 1:5 X(:,i) = exprnd end
可下载资源
生成因变量数据 Y = X * r + eps ，其中 r 只有两个非零分量，噪声 eps 正态分布，标准差为 0.1。
用 拟合交叉验证的模型序列 lasso ，并绘制结果。
Plot(ffo);
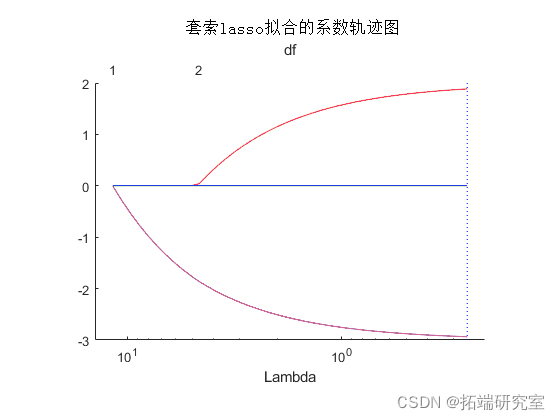
Lambda 该图显示了正则化参数的各种值的回归中的非零系数 。较大的值 Lambda 出现在图的左侧，意味着更多的正则化，导致更少的非零回归系数。
虚线代表最小均方误差的Lambda值（在右边），以及最小均方误差加一个标准差的Lambda值。
后者是Lambda的一个推荐设置。这些线条只在你进行交叉验证时出现。
通过设置’CV’名-值对参数来进行交叉验证。
这个例子使用了10折的交叉验证。
图的上半部分显示了自由度（df），即回归中非零系数的数量，是Lambda的一个函数。在左边，Lambda的大值导致除一个系数外的所有系数都是0。
在右边，所有五个系数都是非零的，尽管该图只清楚显示了两个。其他三个系数非常小，几乎等于0。
对于较小的 Lambda 值（在图中向右），系数值接近最小二乘估计。
求 Lambda 最小交叉验证均方误差加上一个标准差的值。
检查 MSE 和拟合的系数 Lambda 。
MSE(lm)
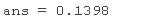
b(:,lam)
随时关注您喜欢的主题
lasso 很好地找到了系数向量 r 。
为了比较，求 r的最小二乘估计 。
rhat
估计 b(:,lam) 的均方误差略大于 rhat 的均方误差 。
res; % 计算残差 MSEmin
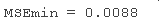
但 b(:,lam) 只有两个非零分量，因此可以对新数据提供更好的预测估计。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python、R语言Lasso、Ridge岭回归、XGBoost分析Airbnb房屋数据：旅游市场差异、价格预测
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
Python个人收入影响因素模型构建：回归、决策树、梯度提升、岭回归
