“应用线性模型”中,我们打算将一种理论(线性模型理论)应用于具体案例。
通常,我会介绍理论的主要观点:假设,主要结果,并进行示范来直观地解释。这里查看一个真实的案例研究,它包含真实数据,2400个观测值,34个变量。

这里只有11个观察值,一个简单的线性模型。让我们对这些数据进行线性回归
最大似然估计,就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
例如:一个麻袋里有白球与黑球,但是我不知道它们之间的比例,那我就有放回的抽取10次,结果我发现我抽到了8次黑球2次白球,我要求最有可能的黑白球之间的比例时,就采取最大似然估计法:
我假设我抽到黑球的概率为p,那得出8次黑球2次白球这个结果的概率为:
P(黑=8)=p^8*(1-p)^2,现在我想要得出p是多少啊,很简单,使得P(黑=8)最大的p就是我要求的结果,接下来求导的的过程就是求极值的过程啦。
可能你会有疑问,为什么要ln一下呢,这是因为ln把乘法变成加法了,且不会改变极值的位置(单调性保持一致嘛)这样求导会方便很多~
同样,这样一道题:设总体X 的概率密度为
已知 X1,X2..Xn是样本观测值,求θ的极大似然估计
P{x1=X1,x2=X2,…xn=Xn}= f(X1,θ)f(X2,θ)…f(Xn,θ)
然后我们就求使得P最大的θ就好啦,一样是求极值的过程,不再赘述。
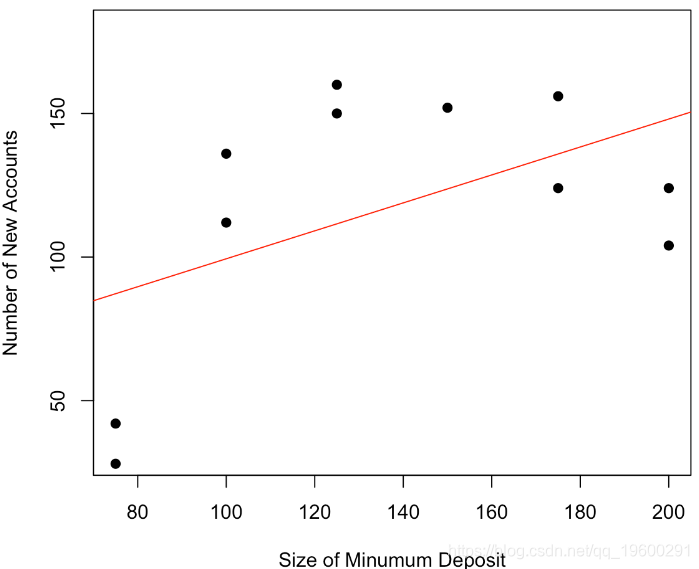
plot(base,pch=19,ylim=c(30,180))
abline(lm(y~x,data=base),col="red")回归线(最大程度地减少误差平方和)是红色曲线
scatter.smooth(x, y,
lpars = list(col = "red")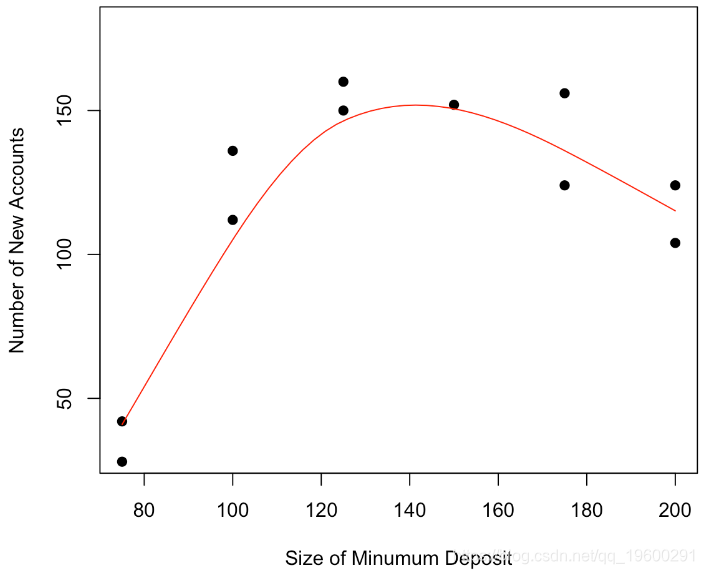
我们可以进一步回答“最大数目在哪里吗”,可以建议一个值,找到一个置信区间吗?
我们可以考虑一个二次模型,换句话说,我们的预测将是 抛物线。
lm(y~x+I(x^2),data=base)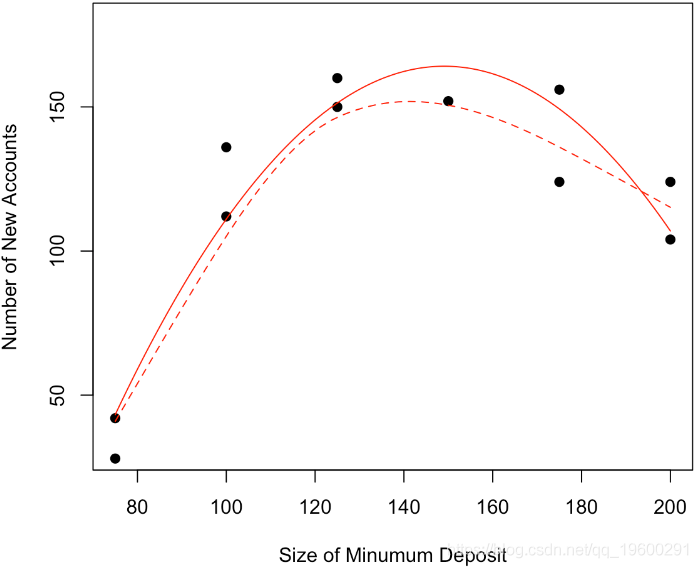
我们可以看到,该模型不仅在视觉上看起来更加符合实际,如果我们看一看回归的结果,该模型也更好
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -3.255e+02 5.589e+01 -5.824 0.000394 ***
x 6.569e+00 8.744e-01 7.513 6.84e-05 ***
I(x^2) -2.203e-02 3.143e-03 -7.011 0.000111 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1现在我们可以证明,对于形式为y =β2×2 +β1x +β0的抛物线,最优值以x⋆=θ= −β1 /2β2来获得。那么θ的自然估计量就是θ= −β 1 /2β2,通过最小化误差平方和。但是如何获得该估计量的方差?通过考虑以下因素,我们自然可以尝试Delta方法
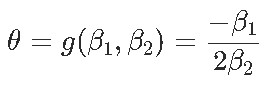
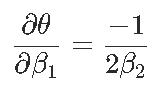
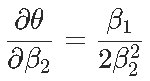
(渐近)方差在这里
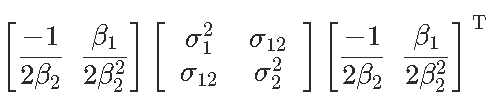
是
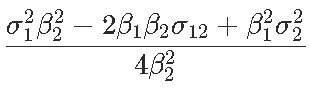
然后我们通过用未知量的估计值替换未知值来获得此渐近方差的估计量。
theta=-beta[2]/(2*beta[3])
theta
[1] 149.0676
s2=t(dg) %*% sigma %*% dg
s2
[,1]
[1,] 94.59911
sqrt(s2)
[,1]
[1,] 9.726207换句话说,如果假设估计量的正态性,我们有以下置信区间
arrows(vx-qt(.975,n-3)*sqrt(s2),vy,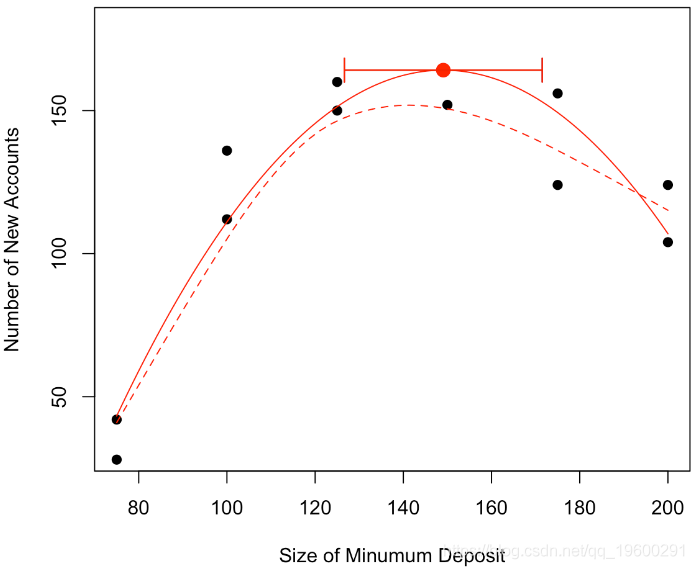
我们还可以尝试另一种策略 。对于我们的二次模型,我们通常在高斯假设下对数似然函数
logL = function(pm){
-sum(log(dnorm (base$y-(b0+b1*base$x+b2*base$x^2)) ,0,b3
}在这里,第一个方法是引入θ(其中抛物线的最大值是)作为模型参数之一-例如代替β2
logL = function(pm){
-sum(log(dnorm( base$y-b0+b1 base$x-.5*b1/theta base$x^2) ,0,b3如果我们寻找最大似然函数,我们得到
optim(par=c(-213,3.5,110,2),logL)
$par
[1] -325.5 6.5 149.0 13.6
$value
[1] 44.3 这与我们之前的计算是一致的。第二个方法是分析似然函数:我们说在多元参数中,一个比另一个更重要。在给定θ的情况下,其他函数才最大化。从技术上讲,参数θ的轮廓对数似然是
logL=function(theta){
-sum(log(dnorm( base$y- b0+b1*base$x-.5*b1/theta*base$x^2 ,0,b3)
optim(par )$value我们可以绘制结果
plot(v1,-v2,type="l",xlim=range(base$x) 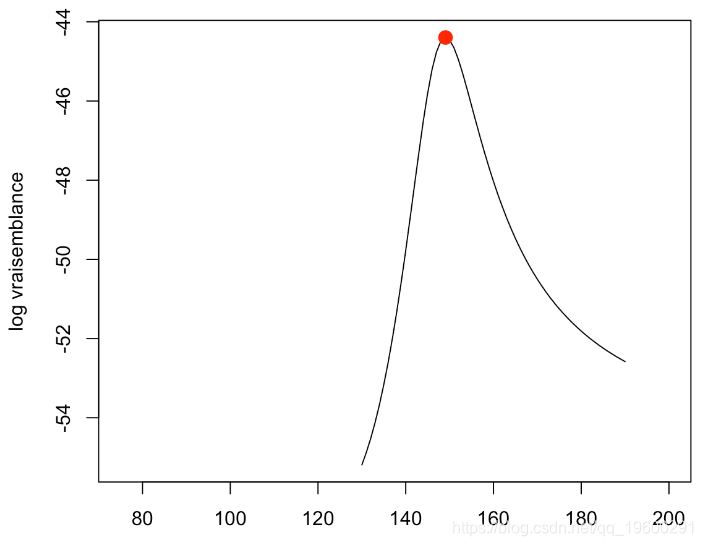
在这里达到最大值
opt
$minimum
[1] 149.068这与我们的计算是一致的。然后,我们可以得到结果的似然比检验。
abline(h=ref,lty=2,col="red")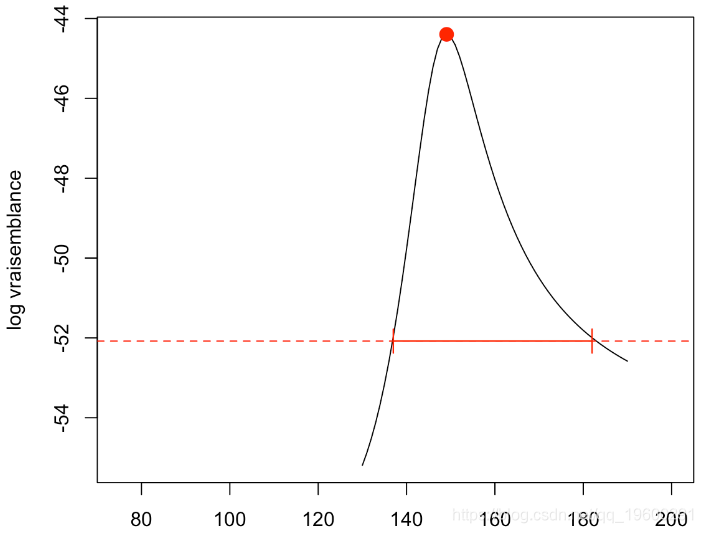
然后我们可以在初始图中绘制置信区间
points(vx,vy,pch=19,cex=1.5,col="red")
arrows(min(v1[id]),vy,max(v1[id]),vy,code=3,angle=90,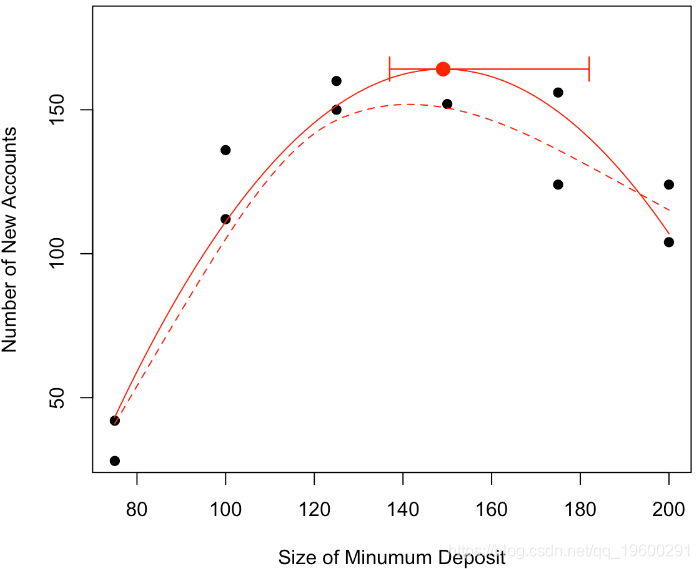
就像大多数统计技术一样,这些都是渐近结果,仅凭11个观察结果无法保证其有效性。
另一个解决方案是使用模拟。我们假设观测值是模型,并且是噪声。我们可以将非参数模型(局部平滑)作为模型并假设高斯噪声。为了生成其他样本,我们将观测值保存在x中,另一方面,对于y,我们将使用y +ε,其中ε将根据正态分布绘制
loess.smooth(x = newbase$x, y= newbase$y
lines(reg$x,reg$y
for(i in 1:20) simu(TRUE)
lines(loess.smooth(x = base$x, y= base$y, evaluation = 501)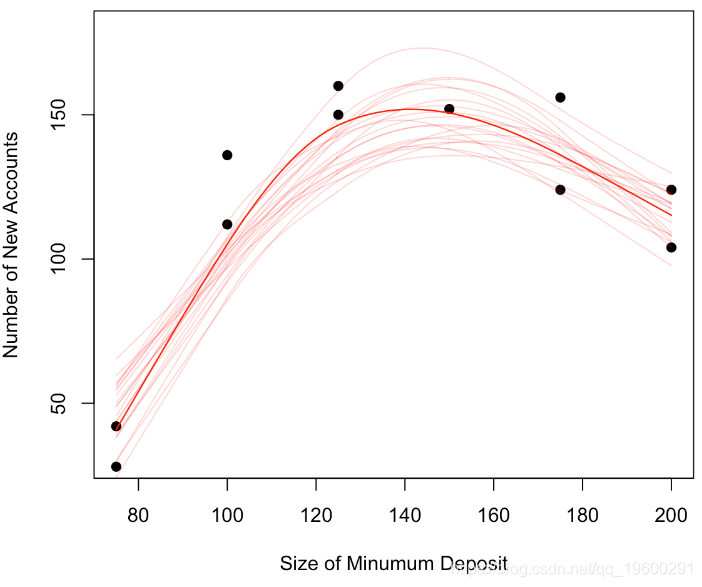
给定数据的不对称性,我们再次使用非参数模型。并且我们通过数值计算最大值。我们重复10,000次。
hist(V,probability = TRUE
lines(density(V) 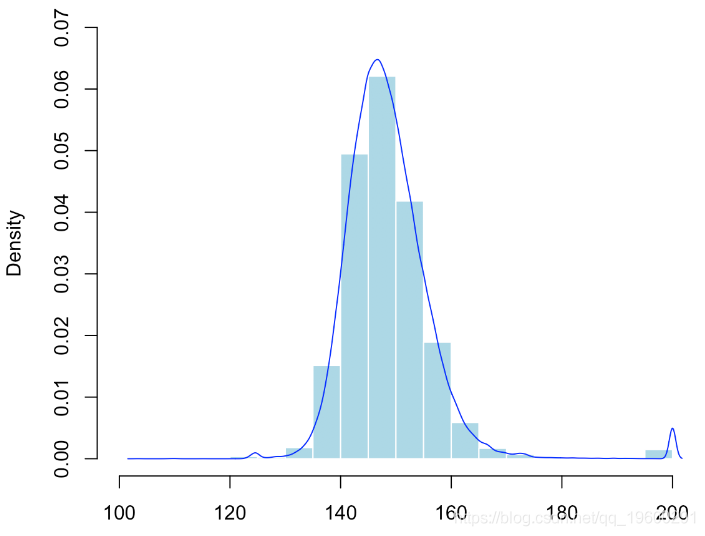
在这里,我们有在10,000个模拟样本上观察到的最大值的经验分布。我们可以通过经验分位数来获得置信区间
arrows(quantile(V,.025 ,vy,quantile(V,.975 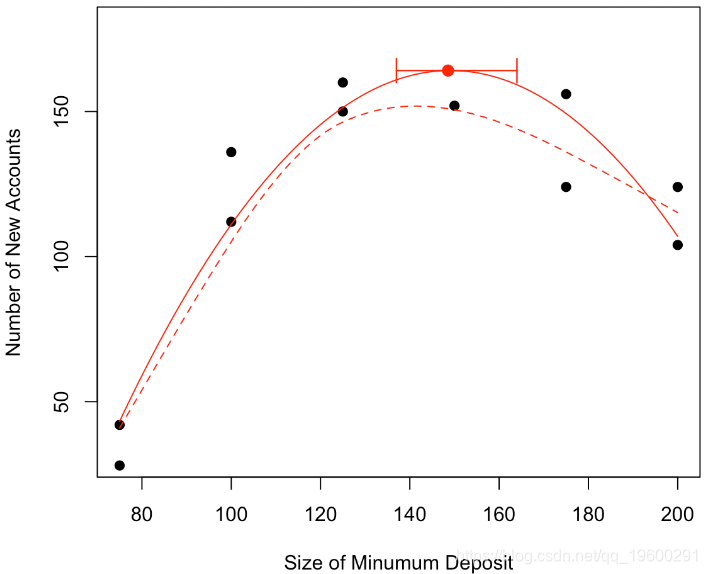
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据 R软件线性模型与lmer混合效应模型对生态学龙类智力测试数据层级结构应用
R软件线性模型与lmer混合效应模型对生态学龙类智力测试数据层级结构应用 R语言非线性方程数值分析生物降解、植物生长数据:多项式、渐近回归、负指数方程、幂函数曲线、米氏方程、逻辑曲线、Gompertz、Weibull曲线
R语言非线性方程数值分析生物降解、植物生长数据:多项式、渐近回归、负指数方程、幂函数曲线、米氏方程、逻辑曲线、Gompertz、Weibull曲线



