
本文档用于比较六个不同统计软件程序(SAS,Stata,HLM,R,SPSS和Mplus)的两级多层(也称分层或层次)线性模型的过程和输出。
下面介绍的六个模型都是两级分层模型的变体,也称为多级模型,这是混合模型的特殊情况。
可下载资源
简介
本文档用于比较六个不同统计软件程序(SAS,Stata,HLM,R,SPSS和Mplus)的两级分层线性模型的过程和输出。
下面介绍的六个模型都是两级分层模型的变体,也称为多级模型,这是混合模型的特殊情况。此比较仅对完全嵌套的数据有效(不适用于交叉或其他设计的数据,可以使用混合模型进行分析)。尽管HLM软件的网站声明可以用于交叉设计,但这尚未得到确认。下面的SAS,Stata,R,SPSS和Mplus中使用的过程是其多层次或混合模型过程的一部分,并且可以扩展为非嵌套数据。
一、简介
1、介绍
分层线性模型 (Hierarchical linear Model,简称 HLM,又称多层线性模型,Multilevel Linear Model)。
HLM常用于社会科学和行为科学,因为它常有嵌套结构(Nested Structure)的数据,因此需用次模型(Sub-Model)或分层线性模型(Hierarchical Model),HLM就是设计来专门解决此类问题的,HLM提供的模型包括2-level models、3-level models、Hierarchical Generalized Linear Models (HGLM)和Hierarchical Multivariate Linear Models (HMLM)等。
二、模型描述
1、模型举例
Level-1 学生层:学生成绩=β0+β1*学生自我效能感+r
Level-2 学校层:β0=γ00+γ01*学校社会经济生活水平+μ1(截距)
β1=γ10+γ11*学校社会经济生活水平+μ2)(斜率)
第一层。学生层的特征变量,是该层想要研究的对应属性(比如:学生家庭社会地位、学生目前学龄等)。系数项代表效应。
第二层。将学生层的系数项,作为下一层的结果因变量,而第二层中的自变量是学校层面的特征。(学校属性,公立、私立学校;学校师资力量程度等)
但是出于比较的目的,我们将仅研究完全嵌套的数据集。除了HLM(完全由GUI运行)以外,所有程序的下面都包含用于每个模型的代码/语法。我们提供了HLM和SPSS的屏幕截图。此外,每个模型均以分层格式和混合格式指定。尽管模型的这两个表达式是等效的,但一些研究领域更倾向于可视化层次结构,因为它更容易看到层次之间的分离,而另一些研究领域则更喜欢混合格式,在其中容易区分固定效果和随机效果。
模型注意事项将预测变量添加到本文档讨论的六个模型中时,我们选择以均值居中为中心,这意味着我们从每个受试者的得分中减去了该变量的总体均值。
正如Enders&Tofighi(2007)所详细讨论的那样,以总体平均值为中心,而不是以组平均值(每个组的平均值均以该组中受试者的得分为准)为中心,并不适合所有模型。 。使用哪种居中方法的选择应由所询问的具体研究问题决定。另一个考虑因素是这些程序使用的估计方法来产生参数估计,即最大似然(ML)或受限最大似然(REML)。每种都有自己的优点和缺点。ML更适合不平衡的数据,但是会产生偏差的结果。REML是无偏的,但是在将两个嵌套模型与似然比检验进行比较时,不能使用REML。
两种方法将产生相同的固定效应估计,但它们对随机效应的估计却有所不同(Albright&Marinova,2010)。正如我们将在下面讨论的模型中看到的那样,这两种方法产生的结果非常相似,并且不会极大地影响随机因素的p值。但是,重要的是要意识到,方法的选择会影响随机因素的估计,标准误差和p值,并且可能会影响宣布随机因素是否重要的决策。SAS,HLM,R和SPSS默认使用REML,而Stata和Mplus使用ML。在本文档中的Stata示例中,我们告诉Stata使用REML以便将输出与其他四个程序进行比较。
类内相关系数
我们还报告了每种模型的类内相关系数(ICC)ρ。ICC是结果变量中方差的比例,由分层模型的分组结构解释。它是根据组级别误差方差与总误差方差之比来计算的:
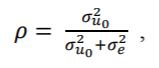
其中,是2级残差的方差,是1级残差的方差。换句话说,与总的无法解释的方差(方差之内和之间)相比,ICC报告了模型中任何可归因于分组变量的预测变量无法解释的变化量。
示例数据集
流行的数据集由来自不同班级的学生组成,并且由于每个学生都属于一个唯一的班级,因此它是一个嵌套设计。因变量是“流行”,它是一个自评的流行度,范围为0-10。预测指标包括学生级别的性别(二分法)和Extrav(连续的自我评价的外向得分),以及班级的Texp(多年的老师经验, 是连续的)。
仅截距模型(无条件模型)
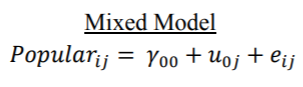
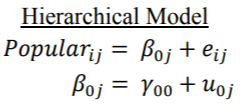
无条件混合模型规范类似于单因素方差分析,其总体均值和类效应。但是,我们将其视为随机效应(均值为零的正态分布变量),而不是像方差分析中那样的固定因子效应。因此,我们将估计值解释为每个类别的平均数在总体平均人气得分附近的方差。
估算值是每个班级的“大众”平均值的平均值,而不是研究中所有学生的平均值。如果数据完全平衡(即每个班级的学生人数相同),则无条件模型的结果将与方差分析程序的结果相同。
SAS结果
proc mixed data=popdata covtest;
model popular = /solution;
random intercept /subject=class type=un;
run;

需要“ covtest”选项来报告方差分量估计的标准误差。另外, 需要指定非结构化协方差矩阵类型,这是HLM和R默认情况下使用的类型,我们在这里使用它进行比较。SAS的输出等于Hox的书表2.1中的结果。我们可以得出结论,各类别之间的平均人气得分为5.078,并且各类别之间的差异(1.221)比不同类别之间的差异(0.702)多。当我们为该模型计算ICC时,将对此进行进一步讨论。
Stata结果
xtmixed popular || class: , variance reml
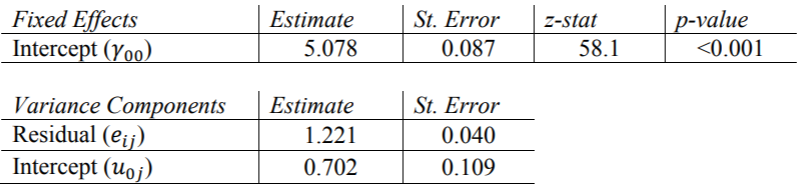
Stata的xtmixed命令需要因变量,后跟“ ||” 指定固定变量和随机变量之间的分隔。我们必须包括方差选项以查看输出中方差分量的估计值,以及reml选项以使用受限的最大似然估计。还要注意,Stata不会输出随机分量估计的p值,但是可以通过置信区间中是否包含零来确定有效值。这些结果与SAS的结果完全匹配
HLM结果
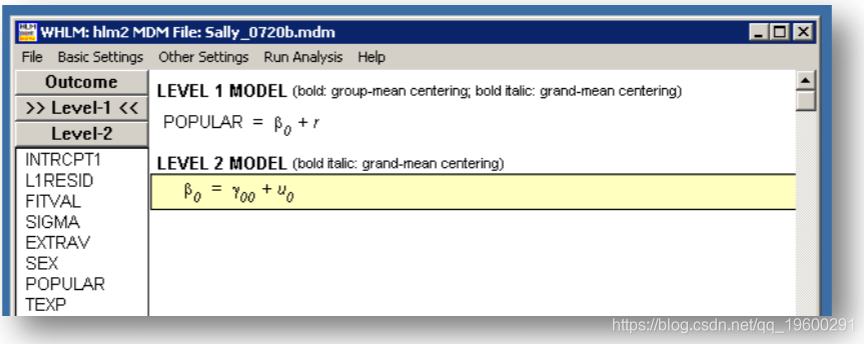
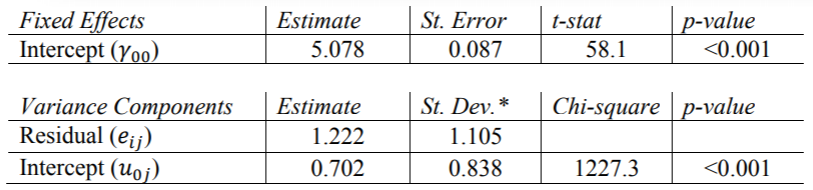
HLM报告方差组件的标准偏差,而不是标准误差。同样,对于随机效应,他 仅报告截距的卡方统计量和p值。这些结果与其他程序的结果相同。
R结果
library(lme4)
library(languageR)
lmer(popular ~ 1 + (1|class))
pvals.fnc(my_intonly)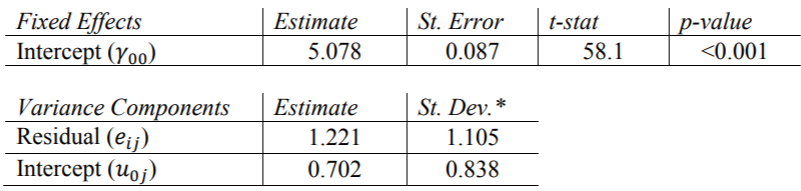
R报告方差成分(例如HLM)的标准偏差,而lme4软件包报告固定效应的t统计量。
SPSS结果
MIXED popular
/FIXED=| SSTYPE(3)
/METHOD=REML
/PRINT=G SOLUTION
/RANDOM=INTERCEPT | SUBJECT(class) COVTYPE(UN).屏幕截图:
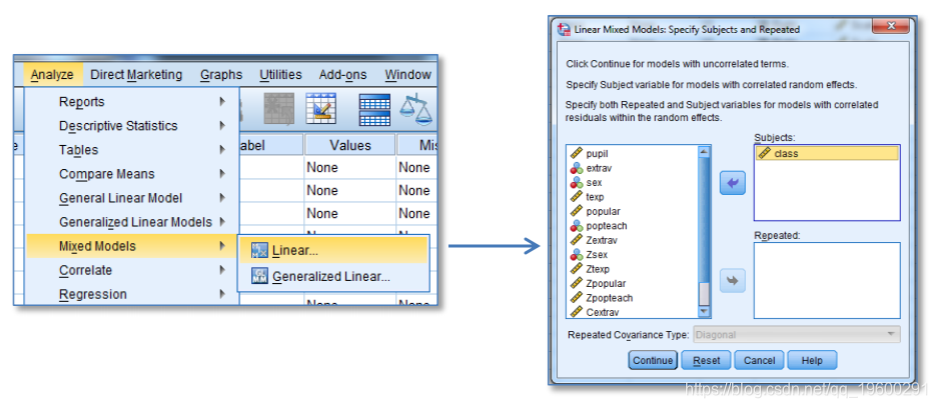

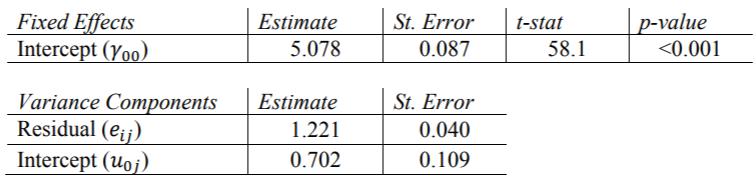
需要在“随机”窗口中指定非结构化协方差类型。这些结果与其他程序和本文得出的结果相同。请注意,像SAS和Mplus一样,SPSS报告方差分量的标准误差,而HLM和R报告标准差。
我们无法得出结论,哪个更适合报告,但是差异不会影响这些参数的p值。
TITLE: HLM Popular Data - Unconditional Model
DATA: FILE IS C:\popular_mplus.csv;
VARIABLE: NAMES ARE pupil class extrav sex texp popular popteach Zextrav
Zsex Ztexp Zpopular Zpopteach Cextrav Ctexp Csex;
USEVARIABLES ARE class popular;
CLUSTER = class;
ANALYSIS: TYPE = twolevel random;
MODEL: %WITHIN%
%BETWEEN%
OUTPUT: sampstat;
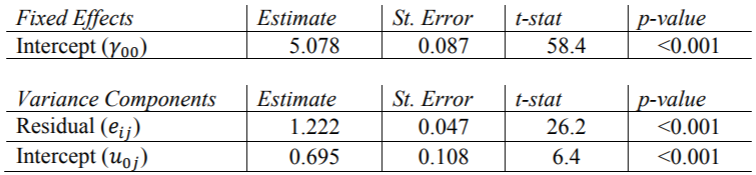
因为这是一个无条件模型,所以我们不需要指定任何WITHIN或BETWEEN变量。下面列出了在MODEL语句中列出变量的标准。在以下各节中,我们将看到前三个示例:
1.%WITHIN%– 1级固定因子(非随机斜率)2.具有潜在斜率变量的%WITHIN%– 1级随机因子3.%BETWEEN%– 2级固定因子4.在任一个陈述–在学生水平上测得的变量,但具有1级和2级方差估计 。
上表显示了Mplus输出底部的“模型结果”部分的结果。Mplus确实会报告每个估计的p值,并且所有估计都与其他程序的p值匹配,但随机截距的方差估计相差约0.007。这种差异是由于Mplus使用ML估计这一事实造成的。尽管存在这种差异,但我们看不到任何变量的重要性发生变化。
汇总
总体而言,这六个程序对于仅截取模型产生了非常相似的结果(唯一的差异发生在随机效应的Mplus估计中)。唯一的区别是他们如何报告随机方差估计的精度。此模型的ICC等于:
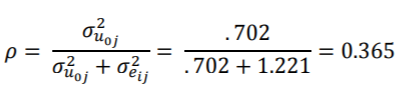
这告诉我们,“流行”课程总变化的大约三分之一可以由每个学生所在的班级解释。
具有一个固定的Level-1因子的随机截距(非随机斜率)模型
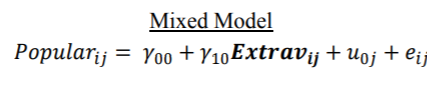

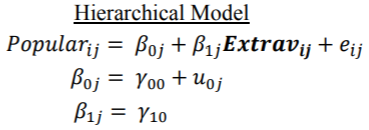

该模型增加了一个学生级别的固定因子Extrav,即自我报告的外向得分。混合模型看起来像是基于带有协变量Extrav的类的ANCOVA,但请记住,我们仍然认为这是随机效应,而不是固定效应。因此, 估算值与ANCOVA程序所得出的估算值不同。
在此数据的实际应用中,Extrav应该具有固定的效果而不是随机的效果是没有意义的,因为学生外向性的水平应随班级而变化。但是,出于比较这四个程序的目的,我们仍然希望调查一个具有一个学生级别固定因子的案例。
随时关注您喜欢的主题
SAS结果
proc mixed data=popdata covtest;
model popular = extrav_c /solution;
random intercept /subject=class type=un;
run;
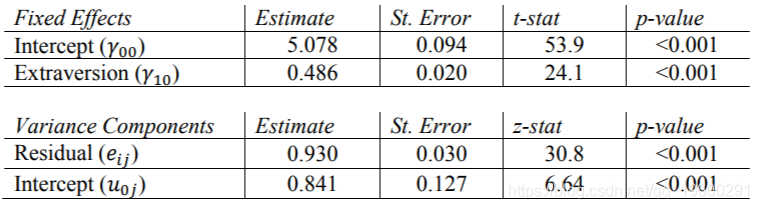

现在,我们对Extrav的固定效果进行了估算。学生报告的外向得分每增加一个单位,他们的受欢迎度得分就会增加0.486。这些结果等于使用REML的其他程序的结果。
Stata结果
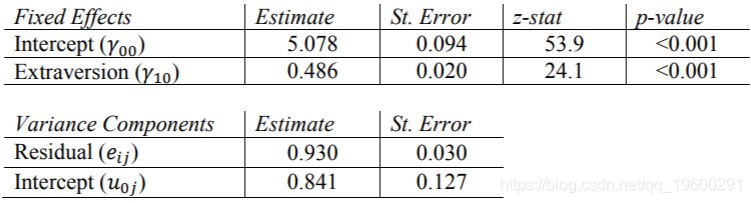

当我们向Stata中的模型添加预测变量时,我们添加了cov(un)选项,指定了非结构化协方差矩阵。我们将 Extraversion变量放在“ ||”之前 表示它是一个固定因子(具有非随机斜率)。这些结果与其他程序的结果相同。
HLM结果
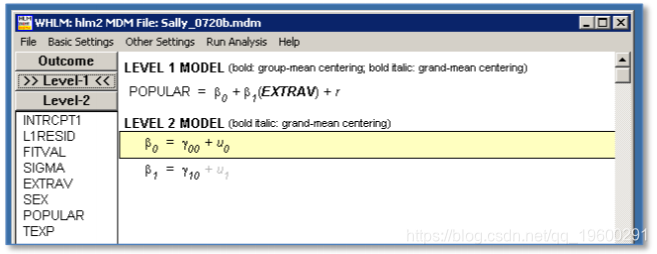

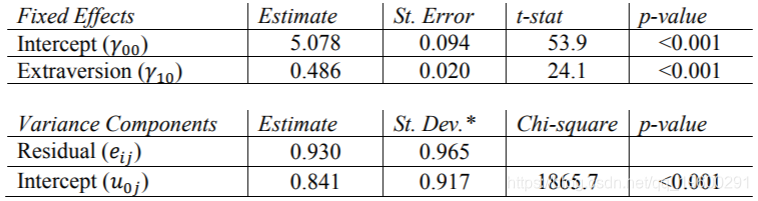

R结果
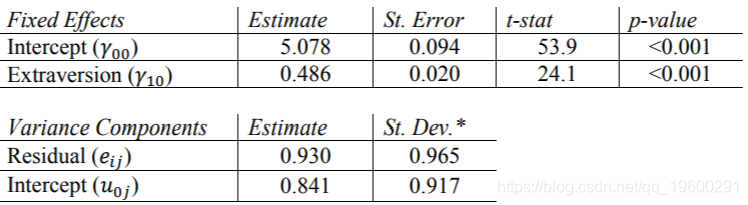

SPSS结果
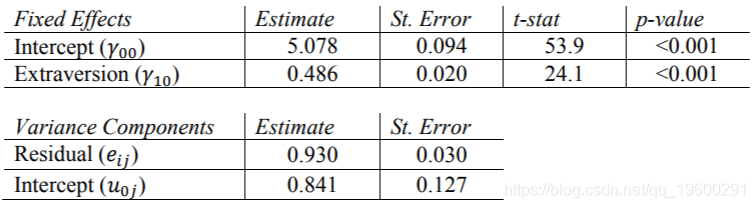

Mplus结果
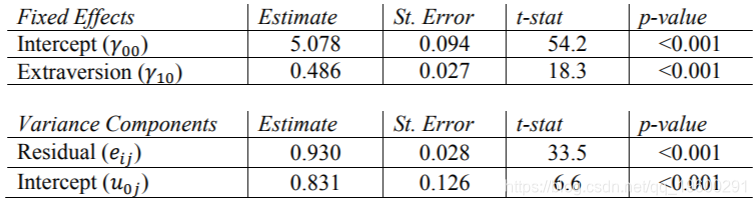

现在,我们在VARIABLE语句的WITHIN选项中包括居中的Extrav变量。对于内部MODEL规范,我们必须使用“ ON”选项,以告知Mplus Extrav是固定的1级因子。 可以看到由于使用ML估计而不是REML,许多估计和估计的标准误差(以及t统计量)存在细微差异。由于方差的估计值与其他程序不同,因此Mplus报告的ICC与下面报告的有所不同。
汇总
对于此模型,前五个程序的结果完全相同,而Mplus的估算值相差很小。此模型的ICC大于无条件模型的ICC(正如预期的那样,因为我们通过添加固定因子来控制某些学生水平的变化):
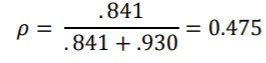

使用一个学生水平的固定因子,“流行”总变化的几乎一半可以由该学生的班级和学生水平的固定因子“外向”解释
一个一级因子的随机截距和斜率模型
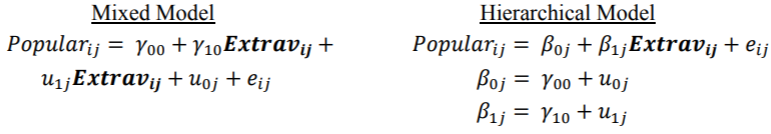

该模型包含Extrav的随机斜率,这意味着我们允许回归方程的斜率随类而变化。该模型比以前的模型更适合于所使用的变量,因为可以直观地假设外向因类而异。
SAS结果
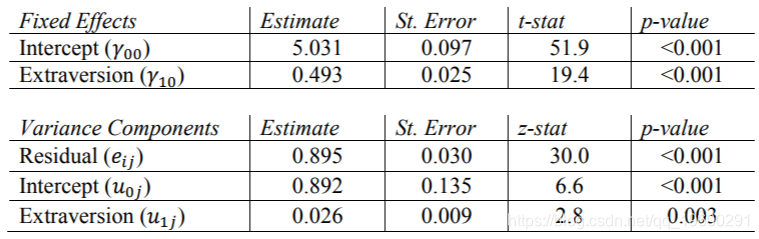

随机Extrav斜率的估计值很重要(p值为0.003),因此我们可以说学生的外向性得分随班级的不同而变化。这些结果与其他程序的结果完全匹配,除了固定效果的t统计量存在一些细微差异。
Stata结果
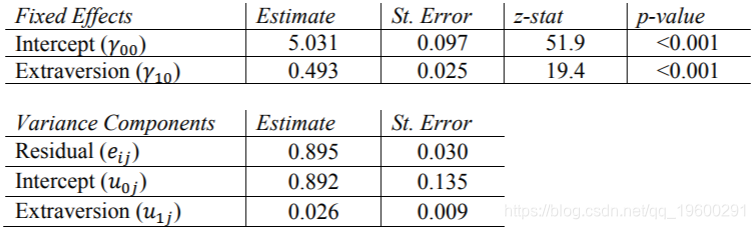

HLM结果
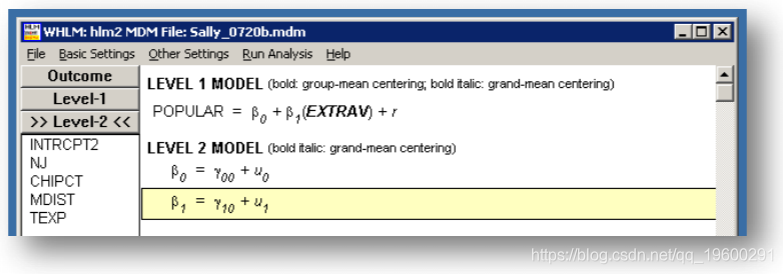

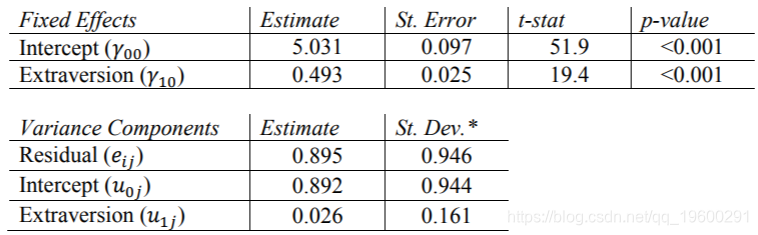

SPSS结果
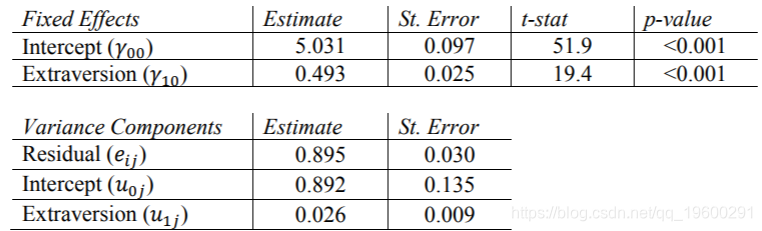

Mplus结果
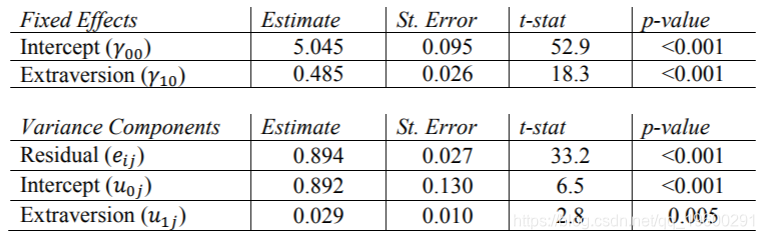

这次我们在WITHIN语句中包括一个潜在的斜率变量,以将Extrav指定为随机因子,该变量告诉Mplus不要在数据集中寻找“ randoms1”,因为没有观察到它。 可以将此变量的输出解释为Extrav的随机斜率分量。我们必须这样做,因为Mplus是为结构方程模型设计的,其多级模型功能是其潜在潜伏分析程序的改编。
汇总
总体而言,前五个程序对该模型产生相同的结果,而Mplus再次由于ML估计而相差很小。此模型的ICC为:
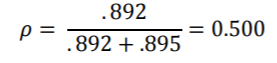

通过将Extrav的影响从固定变为随机,由于我们正在考虑在学生级别上更多随机变化,因此ICC会略有增加。
两个1级因子的随机斜率模型
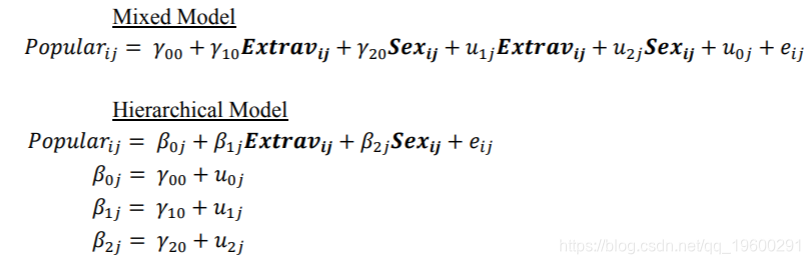
对于此模型,我们包括第二个学生级别的变量Sex,该变量也具有随机斜率。这意味着我们既要考虑学生的性别,又要考虑他们的外向得分,并且允许这两个因素的斜率随班级而变化。
SAS结果


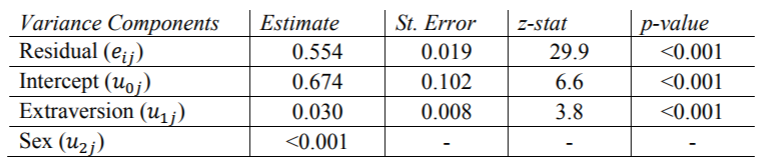

在此输出中,我们可以看到性别确实对学生自我报告的知名度有重大影响(p值<0.001)。对Sex的固定估计意味着,在Extrav不变的情况下,女学生(Sex = 1)的普遍得分比男学生(基线组,Sex = 0)高1.244。
SAS不喜欢在该模型中,Sex的估计方差非常接近零,因此没有输出标准误差或p值。因为非常接近于零,所以我们可以得出结论,性别不会因类别而显着变化。
但是,该输出中的所有估计均与其他程序不同,因此我们选择使用非结构化协方差矩阵规范报告输出。我们不确定这是否是在Stata中运行此类模型的常见问题,但重要的是要意识到它会发生。
Stata结果
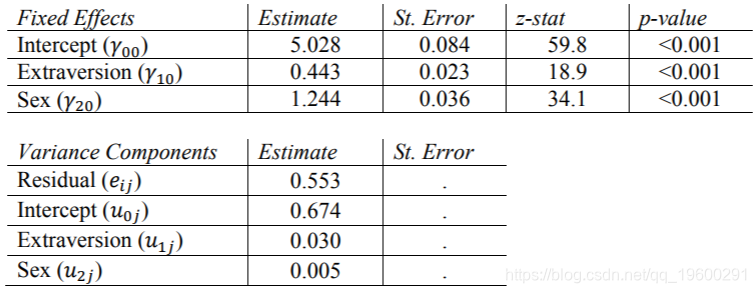
Stata在运行该模型时引用了一个错误:标准误差计算失败,这意味着未计算随机效应的标准误差。我们发现通过删除cov(un)选项,不会出现此错误。
HLM结果
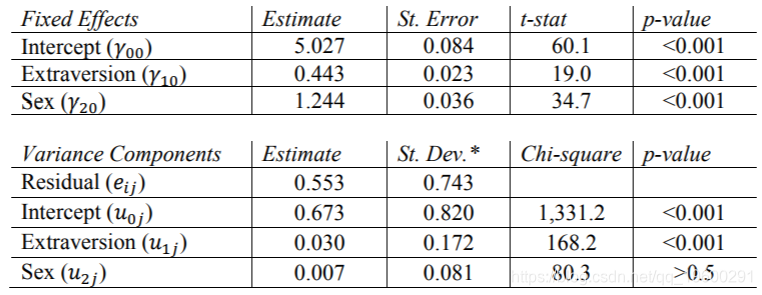
这些估计大致等于其他计划的结果,但随机性别影响的估计除外。由于这种影响非常接近于零,因此程序不会报告完全相同的值,但是所有结果都表明该值远非重要。
R结果


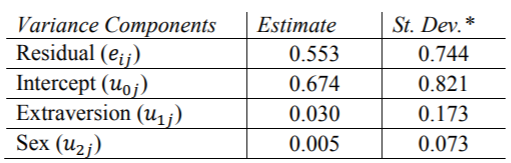

SPSS结果


Mplus结果


这次,我们在WITHIN语句中包括了两个潜在的斜率变量,以将Extrav和Sex指定为随机因子。我们可以将“ randoms1”的输出解释为Extrav的估计,将“ randoms2”的输出解释为Sex的估计。
Mplus针对此模型的输出所得出的估计值与先前模型中的其他程序相距甚远。我们看到,由于模型必须估计更多随机参数,因此估计程序(ML与REML)之间的差异变得更加明显。但是,Mplus同意其他程序的观点,即“性别”的随机方差部分以外的所有估计值都非常重要。
汇总
对于方差非常接近零的随机效应,六个程序以不同的方式处理估计值。SAS和Stata无法报告随机效应的标准误差或p值,而其他变量的估计值和标准误差均具有相当大的差异。Mplus结果也显示出比以前的模型更大的差异。此模型的ICC为:
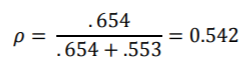

同样,当我们在模型中添加另一个学生级别的效果(包括随机斜率)时,ICC略有增加。
一个2级因子和两个随机1级因子(无交互)
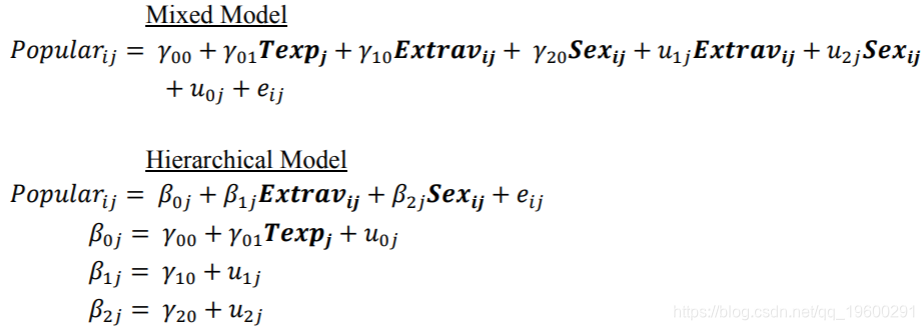

这是我们看到的第一个具有2级(班级)变量的模型:教师的多年经验(Texp),也是以均值为中心的。正如Enders和Tofighi(2007)指出的那样,级别2变量的唯一居中选项是均值居中。 无法对均值中心Texp进行分组,因为它已经在班级水平上进行了度量,这意味着“分组均值”将等于原始值。
在分层中, 可以看到它具有固定的斜率系数,并且对于每个类j都是唯一的。
SAS结果
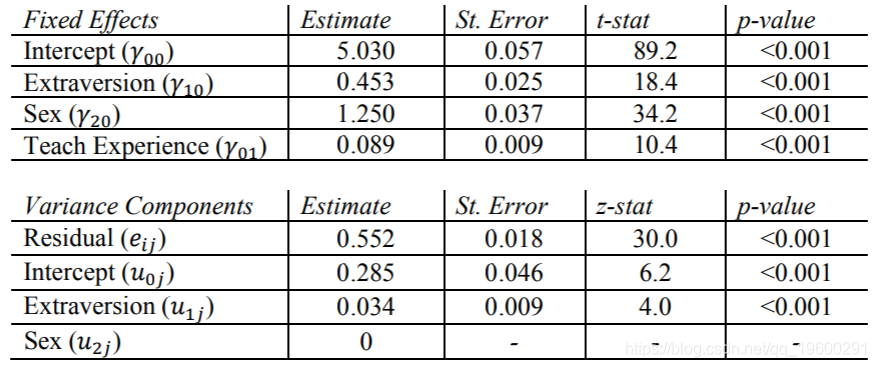
现在,我们在固定效果表中看到了Texp,估计值为0.089,p值很大。这意味着,在使学生的性别和性取向得分保持不变的情况下,每增加一年的教师经验,该学生的热门得分就会增加0.089。
该模型在教师的经验和学生水平的变量之间没有任何相互作用。如果我们有理由相信Texp不会缓和Sex和Extrav对Popular的影响,那么我们将使用此模型,这意味着我们的学生水平变量的斜率是相同的,无论学生是否有新教师或新教师。一位拥有多年经验的人。
同样,我们看到SAS无法处理随机性别效应的很小变化。因此,没有报告标准误差,z统计量或p值。
Stata结果


与以前的模型一样,我们收到一个错误,告诉我们Stata无法计算方差分量的标准误差。但是,这些估计值与其他程序的估计值大致相同。
HLM结果




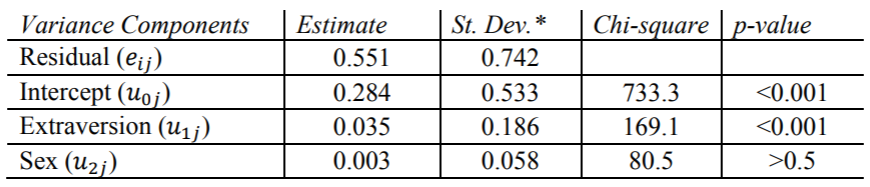

这些估计值与其他程序的结果略有不同 。
R结果
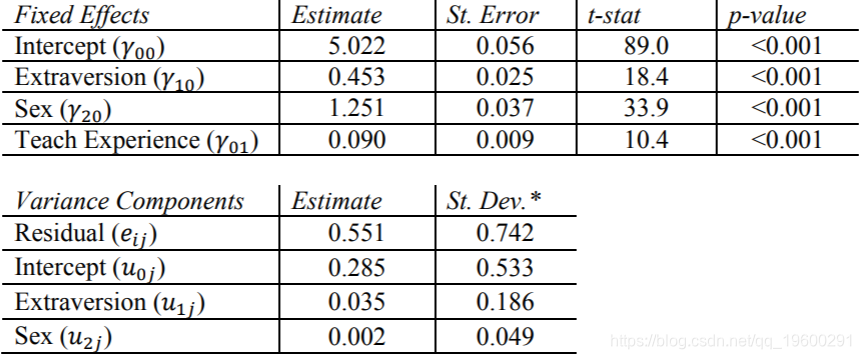

SPSS结果
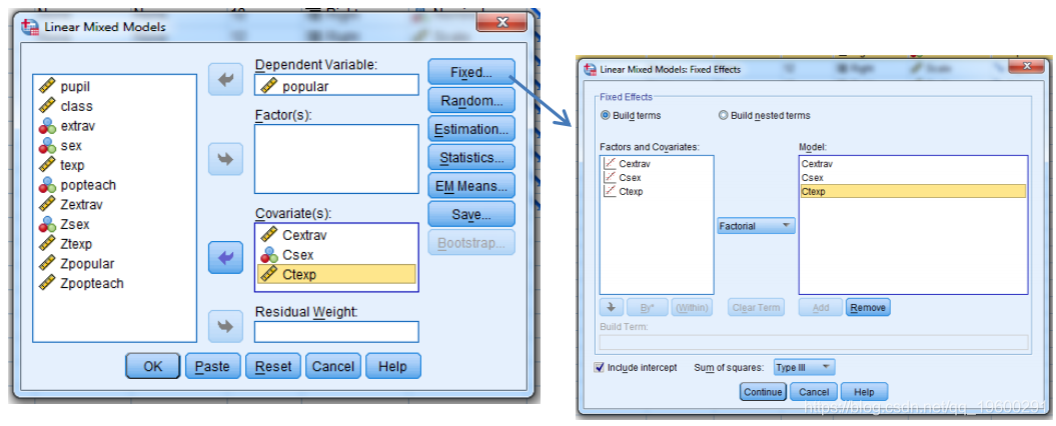

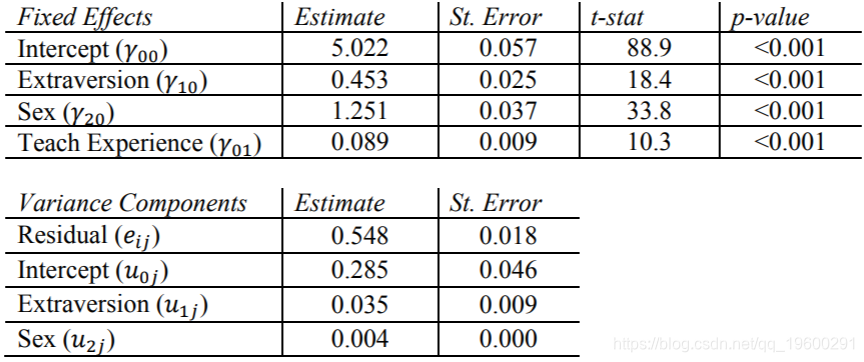

Mplus结果


对于Level-2因子,我们在BETWEEN语句中包括Ctexp。我们再次看到这些估计数与其他五个计划的输出有微小出入
汇总
使用REML的五个程序的输出实质上是相等的,仅相差几千个单位。与以前的模型一样,最大的差异出现在随机性别效应的方差估计中,因为它非常接近零。
请注意,此模型的ICC比以前的模型有所降低(= 0.542):
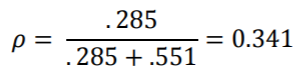

请记住,ICC是衡量 所在的班级可以解释多少无法解释的变化的方法。通过添加班级级别的预测变量,我们可以解释不同班级中较大比例的变化。因此,与没有任何2级预测变量的模型相比,该模型的随机截距存在较少的变异,因此ICC也较低。
具有相互作用的一个2级因子和两个随机1级因子

这是我们在班级变量Texp与学生级变量Sex和Extrav之间进行跨级交互的唯一模型。例如,如果我们想找出具有更多经验的教师是否比新教师对学生的外向性或性别与他们自我报告的知名度之间的关系有不同的影响,则可以使用此模型。换句话说,教师的经历是否适度了性格外向或性别对受欢迎程度的影响?
可以看到,在分层格式中,Texp在三个方程式的每个方程式内都有一个斜率系数。这与混合模型中的交互项有关,即通过外向的教师体验和按性别的教师体验。
SAS结果
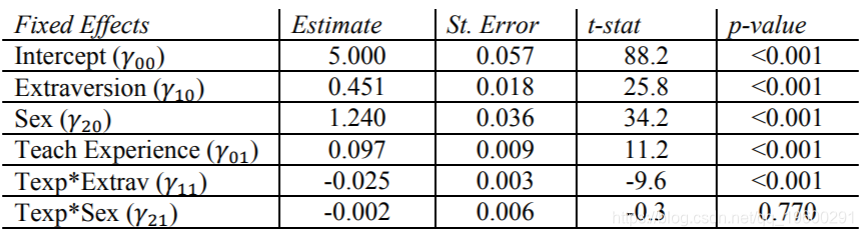

在固定效果表中,有两个交互作用项,其中一个()远不重要,p值> 0.5。
在随机方差分量表中,我们看到外向随机斜率的估计值和性别随机斜率的估计值与零没有显着差异。这意味着没有证据表明这两个因素实际上在该模型中因类别而异。
Stata结果
Stata无法自动识别变量之间的交互项,因此我们必须为两个跨级别的交互手动创建变量(请参见上面的代码中的gen语句)。当我们使用带有非结构化协方差矩阵选项的xtmixed命令运行时,Stata给出了一个错误,指出Hessian不是负半定性,一致性错误,并且没有产生任何输出。
HLM结果

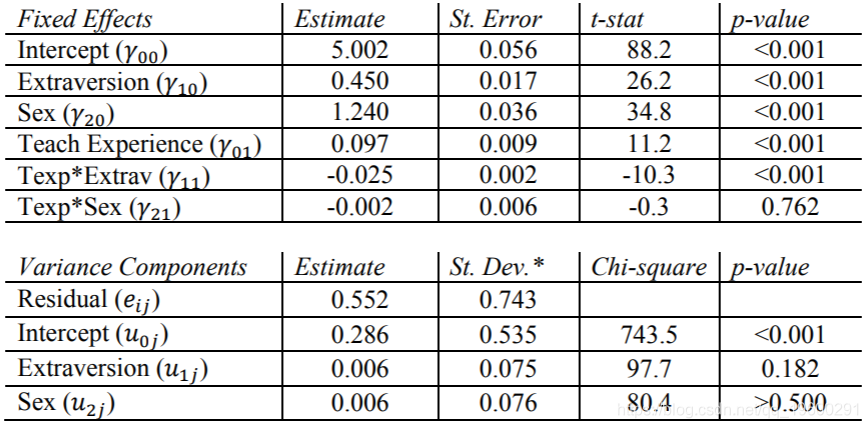
这些估计值大致等于其他程序的结果。
R结果

SPSS结果
对于SPSS 19而言,此模型实在太多了。对于具有非结构化协方差矩阵的更复杂的模型,其他程序可能会运行更有效的算法,因此优于SPSS。
Mplus结果
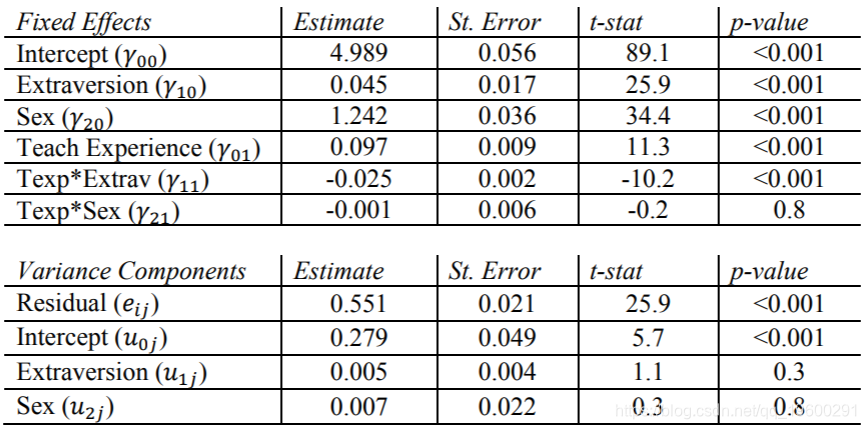
现在,我们在BETWEEN模型部分中包含两个ON语句,以指示与教师经验的跨层次交互。同样,我们发现与其他输出之间的细微差异,但Mplus同意Texp和Sex之间的固定交互作用不显着,而Extrav和Sex的随机组成也并不重要。
汇总
加上两个跨层交互项,Stata和SPSS无法使用非结构化协方差选项运行模型。这并不是说不应该将它们用于这种类型的分析,但是在向具有非结构化协方差矩阵的模型中添加更复杂的参数时,应谨慎使用。
与以前的模型一样,SAS,HLM和R的结果相对接近相等,而Mplus的估计略有不同。另外,ICC与模型5几乎完全相同,这意味着交互作用项不会改变按类别说明的差异比例:
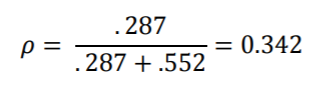
总结
进行比较的目的是调查来自六个不同统计软件程序的嵌套两级层次模型的过程和结果可能存在的差异。总体而言,我们发现SAS,Stata(带有reml选项),HLM,R和SPSS产生的实际估计值之间没有太大差异。Mplus使用另一种估算方法ML,这导致其估算值与其他估算值有所不同。另外,重要的是要注意以下几点:
1.对于方差估计非常接近零的随机效应,SAS无法产生标准误差或p值。其他三个程序在估计这些参数方面的差异与其他效果相比更大。
2. Stata和SPSS无法处理最复杂的模型,该模型包含两个跨级别的交互项。建议使用其他程序来分析复杂模型并指定非结构化协方差矩阵。
此外,我们研究了每种模型中类内相关系数的值。通过添加1级预测因子,ICC有所增加。但是,当我们添加2级预测变量时,ICC会大大降低,甚至比无条件模型更低。这是由于在类级别添加了预测变量时,无法解释的Level-2变异(随机截距项)减少了。
尽管本文档可以用作为嵌套数据集运行各种两级分层模型的指南,但我们强烈建议读者仅在适合回答您的特定研究问题时使用这些模型。在确定固定因素和随机因素之间,以及对于中心平均值为1的总体平均值或组平均值时,必须谨慎使用。
参考文献
Enders, Craig K. and Tofighi, Davood (2007). “Centering Predictor Variables in Cross-Sectional Multilevel Models: A New Look at an Old Issue.” Psychological Methods, vol. 12, pg. 121-138.
Hox, Joop J. (2010). Multilevel Analysis (2nd ed.). New York: Routledge


 Stata空间面板数据模型SAR、中介效应模型、分位数回归分析数字普惠金融指数与农村人均消费支出关系及区域异质性研究|附代码数据
Stata空间面板数据模型SAR、中介效应模型、分位数回归分析数字普惠金融指数与农村人均消费支出关系及区域异质性研究|附代码数据 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 SPSS modeler关联规则、卡方模型探索北京平谷大桃产业发展与电商化研究
SPSS modeler关联规则、卡方模型探索北京平谷大桃产业发展与电商化研究 数据分享|spss modeler用贝叶斯网络分析糯稻品种影响因素数据可视化
数据分享|spss modeler用贝叶斯网络分析糯稻品种影响因素数据可视化



