最近我们被客户要求撰写关于股票收益率时间序列的研究报告,包括一些图形和统计输出。在本文中,我们展示了 copula GARCH 方法拟合模拟数据和股票数据并进行可视化。
r还提供了一个特殊情况(具有正态或学生 t残差)。
一、如何在R中对股票x和y的收益率拟合copula模型
数据集
为了这个例子的目的,我使用了一个简单的股票x和y的收益率数据集(x.txt和y.txt)。
由于金融资产波动剧烈,传统的线性相关建模方法并不能准确度量资产间的相关结构,Sklar提出了Copula函数不仅可以描述金融资产之间非线性相关关系,还消除了对边缘分布和联合分布正态性假设的依赖 [1],因此Copula理论在金融风险度量的研究中得到广泛的应用 [2]。Embrechts等把Copula理论引入到金融风险度量中,且进一步探讨了传统的线性相关系数在实际运用当中的不足,证实了此理论在研究相依关系的有效性 [3] [4] [5]。由于GARCH模型可以刻画金融时间序列的波动聚集现象,Jondeau和Rockinger提出了Copula-GARCH模型,并基于此模型分析国际上四个主要股票市场之间的相关性 [6]。然后国内学者也开始研究Copula理论在金融领域的应用。张尧庭研究分析了Copula模型在我国金融市场的可应用性 [7]。也有学者用Copula函数模型对不同的相依性进行研究 [8] [9],Copula函数是将多个一元分布连接起来构成联合分布的连接函数,度量风险时单个金融资产边缘分布的准确刻画至关重要。GARCH族模型是用以刻画金融时间序列最常用的波动模型,吴振翔等结合Copula和GARCH两个函数优势建立了Copula-GARCH 模型,对我国股票市场的风险进行精准分析 [10]。何其祥等运用Copula-GARCH模型对金融投资组合的风险度量问题进行实证研究 [11] [12] [13] [14] [15]。韦艳华和张世英提出了可用于资产投资组合分析的多元Copula-GARCH模型,结合Monte Carlo模拟法,对上海股市进行了实证研究 [16]。以上学者对投资组合风险的研究主要集中于股票、期货、外汇市场,对开放式基金风险的研究相对较少。因此文中将基于Copula理论对开放式基金的在险价值进行研究。
参考文献
[1] Sklar, A. (1959) Fonctions de répartition àn dimensions et leurs marges. Publication de I’Institut de Statistique de I’Universitd de Paris, 8, 229-231.
[2] Nelsen, R.B. (1998) An Introductions to Copulas. Springer, New York.
[3] Embrechts, P., Mcneil, A. and Straumann, D. (1999) Correlation: Pitfalls and Alternative. Risk-London Risk Magazine Limited, No. 12, 69-71.
[4] Embrechts, P., Hoein, A. and Juri, A. (2003) Using Copula to Bound the Value-at-Risk for Function of Dependent Risks. Finance and Stochastics, 7, 145-167.
https://doi.org/10.1007/s007800200085
[5] Embrechts, P., Lindskog, F. and Mcneil, A. (2002) Modeling Dependence with Copulas and Applications to Risk Management. In: Rachev, S., Ed., Handbook of Heavy Tailed Distributions in Finance, Elsevier, Amsterdam, 329-384.
[6] Jondeau, E. and Rockinger, M. (2006) The Copula-GARCH Model of Conditional Dependencies: An International Stock Market Application. Journal of International Money and Finance, 25, 827-853.
https://doi.org/10.1016/j.jimonfin.2006.04.007
[7] 张尧庭. 连接函数(Copula)技术与金融风险分析[J]. 统计研究, 2002(4): 48-51.
[8] 童中文, 何建敏. 基于Copula风险中性校准的违约相关性研究[J]. 中国管理科学, 2008, 16(5): 22-27.
[9] 刘琼芳, 张宗义. 基于Copula房地产与金融行业的股票相关性研究[J]. 管理工程学报, 2011, 25(1): 165-169+164.
[10] 吴振翔, 陈敏, 叶五一, 缪柏其. 基于Copula-GARCH 的投资组合风险分析[J]. 系统工程理论与实践, 2006, 26(3): 45-52.
[11] 何其祥, 张晗, 郑明. 包含股指期货的投资组合之风险研究——Copula方法在金融风险管理中的应用[J]. 数理统计与管理, 2009, 28(1): 159-166.
[12] 史道济, 李璠. 基于Copula的股票市场VaR和最优投资组合分析[J]. 天津理工大学学报, 2007, 23(3): 13-16.
[13] 李楠. 外汇投资组合的风险分析[D]: [硕士学位论文]. 天津: 天津财经大学, 2014.
[14] 刘红玉. 基于Copula-GARCH的投资组合风险度量的实证应用[J]. 齐齐哈尔大学学报, 2015, 31(1): 73-76.
[15] 曹境鸽. 基于Copula-GARCH模型的ETF基金相关性风险研究[D]: [硕士学位论文]. 北京: 首都经济贸易大学, 2018.
[16] 韦艳华, 张世英. 多元Copula-GARCH模型及其在金融风险分析上的应用[J]. 数理统计与管理, 2007, 26(3): 432-439.
首先,我们需要加载数据并将其转换成矩阵格式。也可以选择绘制数据。
x <- read.table
y <- read.table
# 实际观察结果
plot
数据的图表
视频
时间序列分析模型 ARIMA-ARCH GARCH模型分析股票价格数据
视频
量化交易陷阱和R语言改进股票配对交易策略分析中国股市投资组合

现在我们已经加载了我们的数据,可以清楚地看到,存在正相关。
下一步是拟合。为了拟合数据,我们需要选择一个copula模型。该模型应根据数据的结构和其他因素来选择。作为第一种近似值,我们可以说我们的数据显示了正相关,因此一个可以复制这种相关的copula模型应该是不错的。我选择使用正态copula。对于其他类型的copula模型来说,拟合过程是相同的。
让我们来拟合数据
# 正态Copula
normalCopula
fiop<- fit
# 系数
rho <- coef
print
请注意,数据必须通过函数pobs()输入,该函数将真实观测值转换为单位平方[0,1]的伪观测值。
还要注意的是,我们使用的是 “ml “方法(最大似然法),但是也有其他方法,如 “itau”。

在我们的例子中,拟合的协整参数rho等于0.73。让我们模拟一些伪观察结果

通过绘制伪观测值和模拟观测值,我们可以看到使用copula的模拟与伪观测值的匹配情况。
# 伪观察
pobs
plot
# 模拟数据
u1 = rCopula
随时关注您喜欢的主题
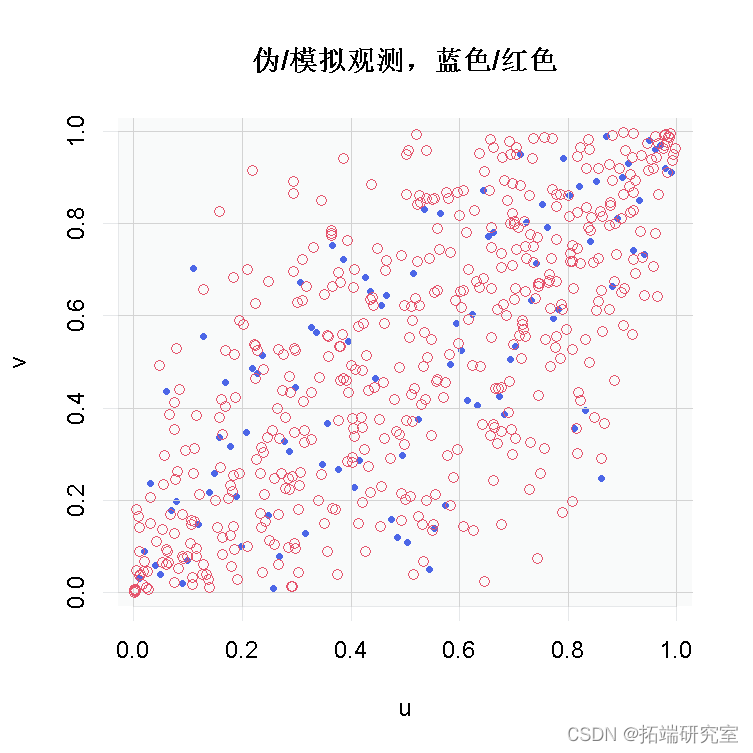
这个特定的copula可能不是最好的,因为它显示了严重的尾部相关性,而这在我们的数据中并不强烈,不过这只是一个开始。
在开始的时候,我们可以选择将数据与每个随机变量的分布画在一起,如下所示
# 用柱状图绘制数据 hst <- hist top <- max layout par plot barplot
并得到我们的原始数据集的这种表现形式

将 t copula 拟合到标准化残差 Z。对于边缘分布,我们还假设 t分布,但具有不同的自由度;为简单起见,此处省略了估计。

n <- rep # 边际自由度;为了简单起见,这里使用已知的自由度 es <- cbind # 拟合与真实 rownames

从拟合的时间序列模型中模拟
从拟合的 copula 模型进行模拟。
并为每个边缘绘制结果序列 (Xt)
X <- sapply # 模拟序列X_t matplot

二、模拟数据
首先,我们模拟了分布。为了演示的目的,我们选择了一个小的样本量。
##模拟 Copula # 定义copula对象 set.seed(21) # 可重复性 # 对copula进行采样 sqrt * qt # 对于ugarchpath()来说,边际必须具有均值0和方差1!
现在我们使用依赖于 copula 来模拟两个 ARMA(1,1)-GARCH(1,1) 过程。 ARMA(p1,q1)-GARCH(p2,q2) 模型由下式给出

## 固定边缘模型的参数 fixedp <- list var <- list(model = "sGARCH") # 标准GARCH garch # 条件创新密度(或者使用,例如,"std")。 ## 使用从属创新模拟ARMA-GARCH模型 garch n.sim = n, # 模拟的路径长度 m.sim = d, # 要模拟的路径数量 ##提取结果系列 fit# X\_t = mu\_t + eps_t (模拟过程) sig # sigma_t (条件性标准偏差) resid # epsilon\_t = sigma\_t * Z_t (残差) ## 绘制 matplot

基于模拟数据的拟合
我们现在展示如何将 ARMA(1,1)-GARCH(1,1) 过程拟合到 X
garchspec fit <- apply
检查(标准化的)Z,即残差Z的伪观测值。
Z <- sapply U <- pobs plot

将 t copula 拟合到标准化残差 Z。对于边缘分布,我们还假设 t分布,但具有不同的自由度;为简单起见,此处省略了估计。
fitCopula

n <- rep # 边际自由度;为了简单起见,这里使用已知的自由度 es <- cbind # 拟合与真实 rownames

从拟合的时间序列模型中模拟
从拟合的 copula 模型进行模拟。
set.seed(21) # 可重复性 U <- rCopula Z. <- sapply ## => 标准化的garchsim() sim <- lapply
并为每个边缘绘制结果序列 (Xt)
X <- sapply # 模拟序列X_t matplot


可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化
Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 专题|LSTM-XGBoost,ARMA-LSTM,LDA-LSTM黄金比特币价格混合预测,蔬菜包发放时空协同调配,知乎综艺评论情感时序洞察
专题|LSTM-XGBoost,ARMA-LSTM,LDA-LSTM黄金比特币价格混合预测,蔬菜包发放时空协同调配,知乎综艺评论情感时序洞察 Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据


