本教程将介绍如何使用SAS进行单因素方差分析。
我们想研究不同疗法对焦虑症的有效性。我们收集了以下类别的75个样本：
可下载资源
我们想研究不同疗法对焦虑症的有效性。我们收集了以下类别的75个样本：
- 无处理（ñ1n1 = 27）。
- 生物反馈（ñ2n2 = 24）。
- 认知行为治疗（n3n3 = 24）。
因变量是焦虑水平。零假设是所有三个均值均相等。
- H0H0：μ1=μ2=μ3μ1=μ2=μ3
- HAHA：至少有两个μiμi的是不同
如果甚至两种方法均存在显着差异，我们将拒绝原假设。
SAS中的单因素ANOVA
我们可以使用条形图将数据可视化，以检查组之间方差的正态性和均等性。当我们运行ANOVA时，SAS会自动打印。
我们可以进行方差分析并查看以下结果：
proc anova data=anova;
class treatment;
model anxiety = treatment;
means treatment / tukey;
run; 
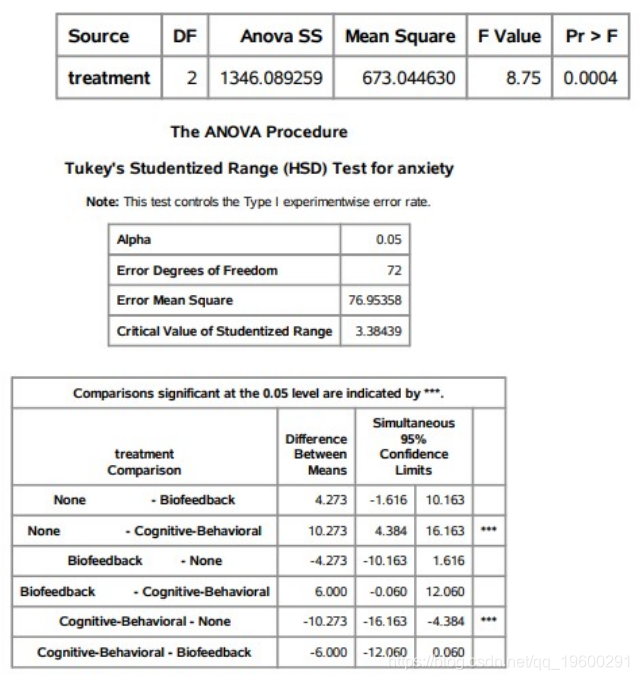
该class声明告诉SAS处理是一个类别变量。该means语句将提供所有成对比较，并使用Tukey方法调整p值。
这将为我们提供下图：
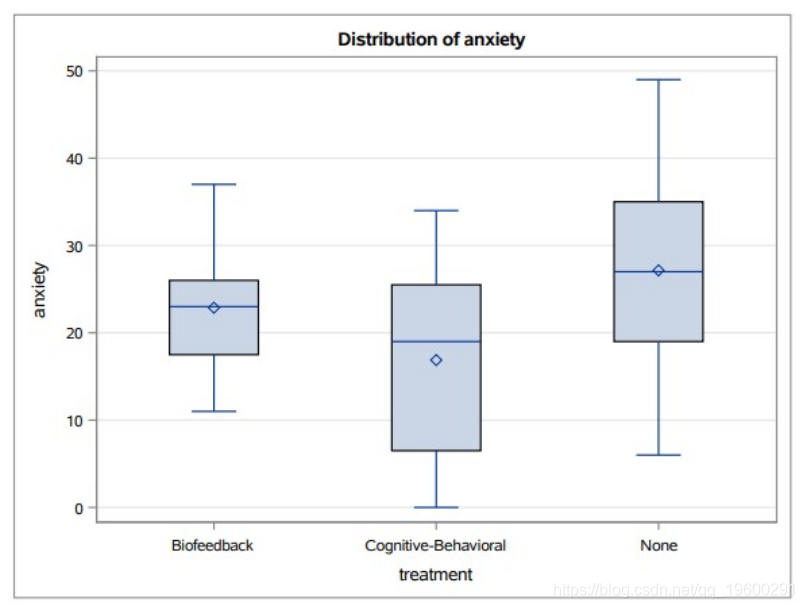
常态看起来不错。方差齐次性假设似乎令人怀疑（可以测试）。我们还将获得以下输出：
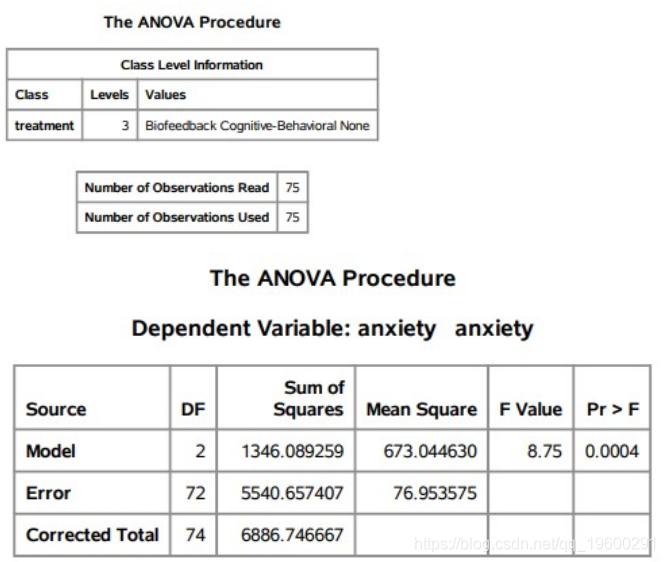
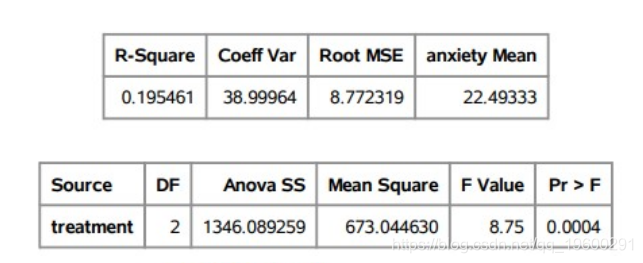
前两个表给出了类别级别变量（处理）及其可能的级别（1、2或3），以及所使用的观察次数（n=75n=75）。
FFFFdf1 df2 df p<.001 p<.001μi
R语言用逻辑回归预测BRFSS中风数据、方差分析anova、ROC曲线AUC、可视化探索
R语言分析糖尿病数据：多元线性模型、MANOVA、决策树、典型判别分析、HE图、Box’s M检验可视化
SAS数据挖掘EM贷款违约预测分析：逐步Logistic逻辑回归、决策树、随机森林
SAS与eviews用ARIMA模型对我国大豆产量时间序列预测、稳定性、白噪声检验可视化
