本文包含一些直观的示例来说明 copula 理论的核心概念。
以下是脚本及其各自用途的简短列表：
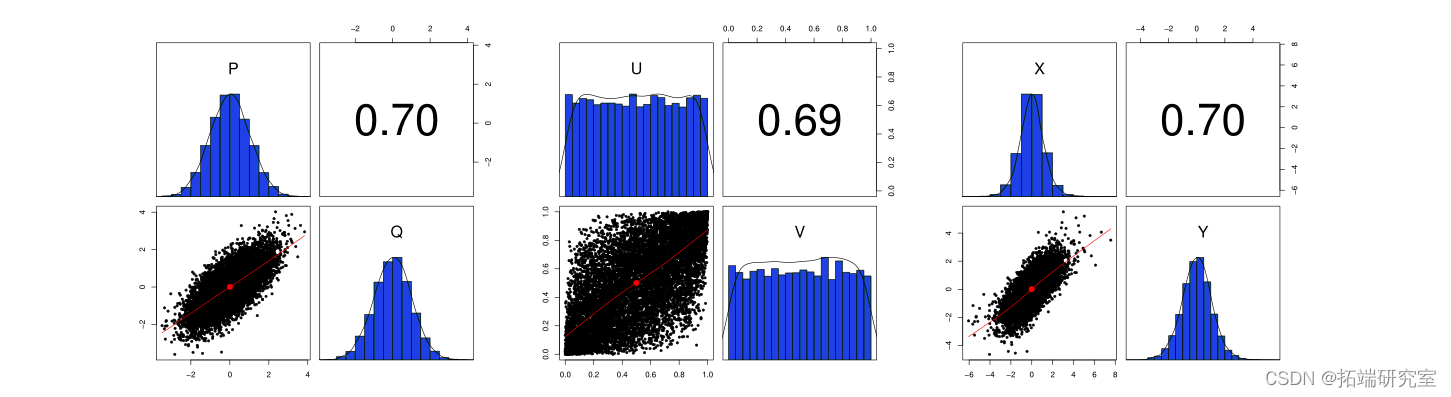
- 首先演示如何使用高斯 copula 来模拟具有任意边际分布的两个相关随机变量。
它使用基本的 R 代码实现了这一点，因此无需使用 copula 包来揭开这个概念的神秘面纱。
library(MASS) # 用于从多元法线绘制 set.seed(206) # 确保可重复性 d <- 2 # 随机变量的数量 n <- 10000 # 样本数 v <- pnorm(pq) # 概率积分变换 ################################################# ##### x <- qt(v\[, 1\], df = 7) # 用学生 t 的分位数函数变换 (smirnov) 第一个 rv，其中 nu = 7 y <- qt(v\[, 2\], df = 15) # 用 nu = 15 的学生 t 的分位数函数变换 (smirnov) 第二个 rv pair.panels(xy, rug = FALSE, cex.cor = 0.7, hist.col = "dodgerblue4") # 绘图
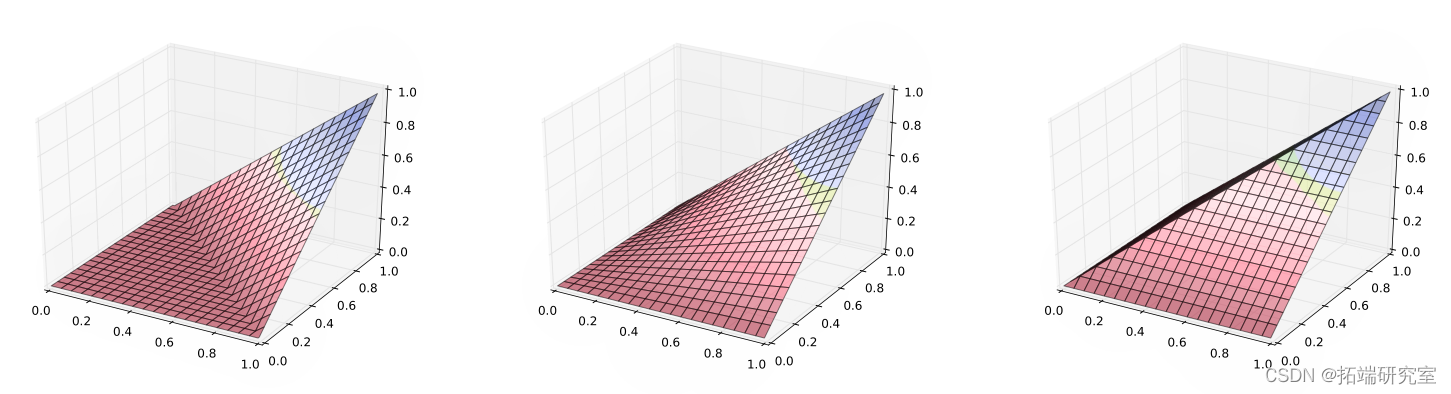
- Python 脚本，可在双变量设置中生成三个基本 copula（反单调性、独立性和同调性）的 3D 可视化。反单调性 copula 构成了 Fréchet-Hoeffding 下界，而同调性 copula 构成了 Fréchet-Hoeffding 上界。
### 定义 3 个基本的 Copula 函数 ### Z = np.maximum(X + Y - 1, 0) Z = X * Y 定义上限（X，Y）： Z = np.minimum(X, Y) ### 创建数据点### X, Y = np.meshgrid(x, y) # 创建“基础网格” Z = upperBound(X, Y) # z 轴上的点 ### 绘图### plot_surface(X, Y, Z1
- 加强您对 copula 类和族的理解。通过使用散点图，我们强调了 Gaussian、t、Clayton 和 Gumbel copula 之间的差异。
随时关注您喜欢的主题
＃ 清理 set.seed(206) # 确保可重复性 # 创建 copula 对象 normalCopula(param = 0.7, dim = 2) # 模拟 n <- rCopula(10000, normCop) # 绘图 par(mfrow = c(2, 2)) plot(R\[, 1\], R\[, 2\], pch='.', col='dodgerblue4', xlab = "", ylab = "",)
- 绘制了“copula”的文献计量分析使用情况。
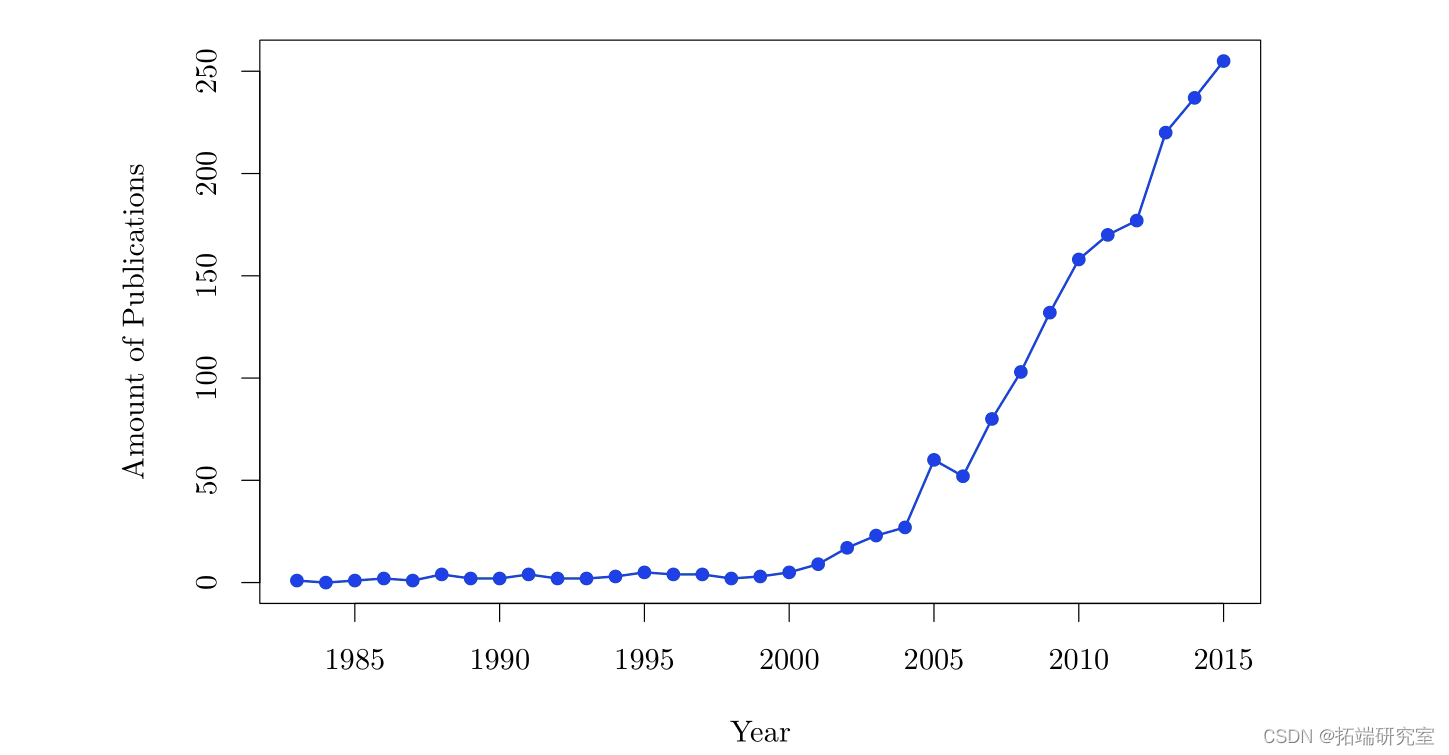
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
R语言股价跳跃点识别：隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析
【视频讲解】Python用LSTM长短期记忆网络GARCH对SPX指数金融时间序列波动率滚动预测
