最近我们被客户要求撰写关于copulas的研究报告。这篇文章是关于 copulas 和重尾的。
在全球金融危机之前，许多投资者是多元化的。
看看下面这张熟悉的图：
黑线是近似正态的。红线代表Cauchy分布，它是具有一个自由度的T分布的一个特殊情况。
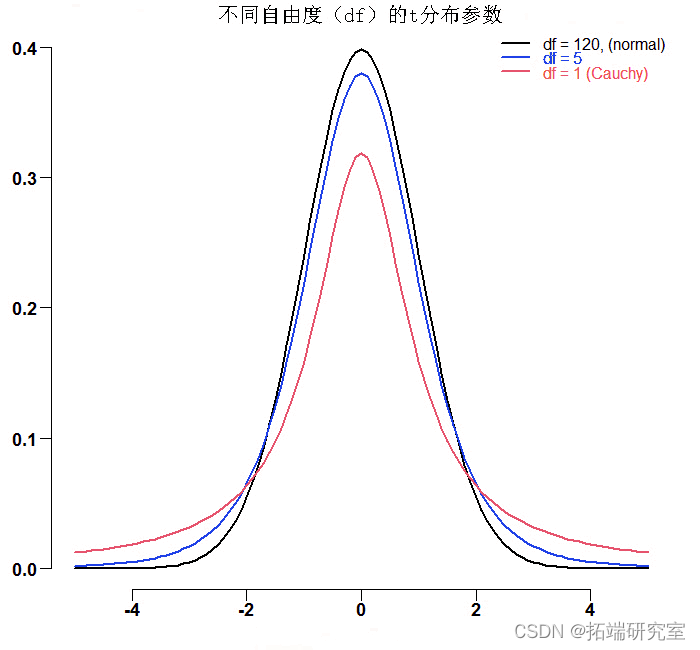
也许是因为Cauchy和t分布混在一起。我们总是可以计算出经验方差。请看下图。这是对1自由度的t分布（红色的Cauchy分布）和5自由度的t分布（蓝色）的模拟结果。
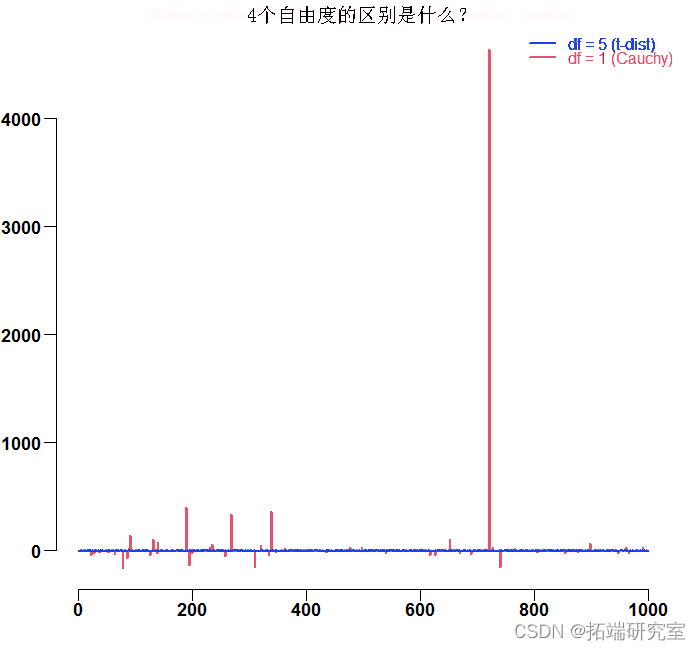
为了比较不同的尾部行为，我们有我们所谓的尾部指数。简而言之，在几乎任何分布中，某个阈值之后的观测值（比如说最差的5%的情况下的观测值）都是渐进式的帕累托分布。
![[F(x) = Pr(X > x) = \left{ \begin{array}{rl} (\frac{x_m}{x} )^ \alpha & \; \mbox{ if $ x \geq x_m$}, \ 1 & \qquad \mbox{if $x < x_m$,} \end{array} \right]](https://img-blog.csdnimg.cn/img_convert/ae15be9b9942853adf8e2ba3d92c9f0f.png "[F(x) = Pr(X > x) = \left{ \begin{array}{rl} (\frac{x_m}{x} )^ \alpha & \; \mbox{ if $ x \geq x_m$}, \ 1 & \qquad \mbox{if $x < x_m$,} \end{array} \right]")
其中x_m是截止点，α将决定尾巴的形状。α也被称为尾部指数。
随时关注您喜欢的主题
现在大家都知道，金融收益呈现出厚尾。这使得保持投资组合为左尾事件做好准备变得更加重要，因为在那个区域，由于相关性的增加，你会同时受到所有资产的影响（正如金融危机所证明的那样）。
在这个讨论中，_copulas_发挥了重要的作用。
_copulas_的概念是相当巧妙的。copula这个词起源于拉丁语，它的意思是捆绑。
当我们有两个（或更多）资产类别的收益，我们可以假设或模拟它们的分布。
做完这些之后，我们可以把它们 “粘贴 “在一起，只对相关部分进行建模，而不考虑我们最初对它们各自分布的建模方式。怎么做？
我们从英国统计学家 Ronald Fisher 开始，他在 1925 年证明了一个非常有用的性质，即任何连续随机变量的累积分布函数都是均匀分布的。形式上，对于任何随机变量 X，如果我们表示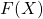 
作为 X 的累积分布，则 
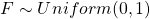。请记住，当我们说 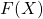，它仅意味着概率， 
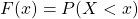。这就是 [0,1] 的来源，因为它只是一个概率。从三种不同的分布进行模拟：指数、伽玛和学生-t，变换它们并绘制直方图：
par(mfrow=c(3,1)) # 分割屏幕 apply(tm, 2, hist,xlab="", col = "azue") # 绘制
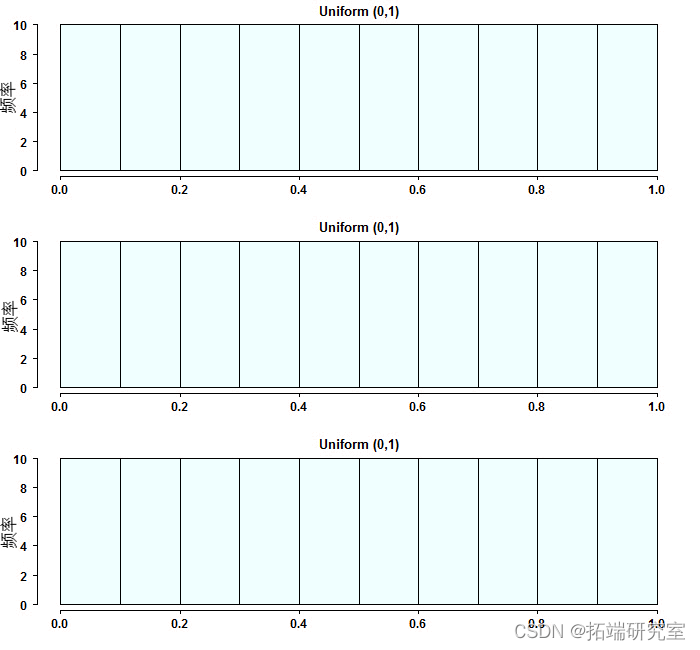
您可以通过这种方式转换任何连续分布。现在，将两个变换后的随机数表示为 u和 v。我们可以将它们“绑定”（copula）： C(u,v)。 其中， C是一些函数，并且因为原始变量是“不可见的”（当我们将其转换为 Uniform 时消失了），所以我们现在只讨论两个变量之间的相关性。例如 ，C可以是具有一些相关参数的二元正态分布。我不会在这里写出双变量正态密度，但它只是一个密度，因此，它将说明在中心地带观察到两个变量在一起的概率，和/或在尾部一起的概率。这是绕过原始变量的分布，只谈相关结构的一种方式。
现在让我们对金融和消费必需品之间的相关结构进行建模。从拉取数据开始：
da0 = (getSymbols(sym\[1\])
for (i in 1:l){
da0 = getSymbols
w <- dailyReturn
w0 <- cbind(w0,w1)
}
apply(rt0, 2, mean) # 定义平均数
apply(rt0, 2, var) # 和标准差
cor(et0) # 无条件的相关关系。
我们现在要做的是按照讨论的方法对数据进行转换（称之为概率积分转换），并将其绘制出来。同时，我们模拟两个具有相同（量化-非条件）相关性的随机常模，并比较这两个数字。
desiy <- kde2d contour # 现在从两个具有相同相关性进行模拟。 smnom <- rmvnorm trnorim_rm <- appl mdni_im <- kde2d plot contour title
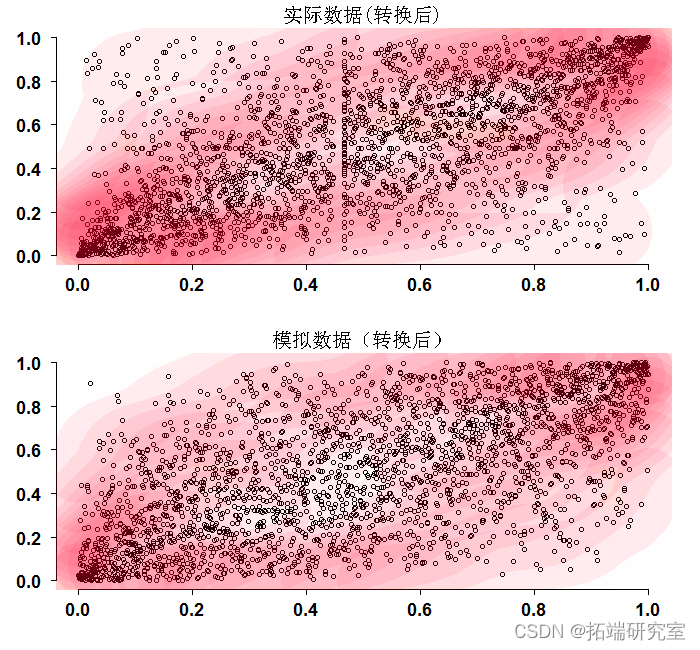
乍一看，这两个数字看起来差不多。但更详细的观察发现，角落更快地收敛到（0,0）、（1,1）坐标。这也是由这些区域的深色等值线颜色表明的。请记住，模拟数据使用的是与真实数据相同的经验相关性，所以我们在这里讨论的其实只是结构。
现在让我们生成一个copula函数
，我们可以用它来 “包裹 “或 “捆绑 “我们的转换后的收益。我们定义了一个重尾（df=1）和一个轻尾（df=6）的copula。我们可以直观地看到这个函数实际上是什么样子的。这样做的方式与我们可视化正态密度的方式差不多，但现在因为它是一个双变量函数，所以它是一个三维图。
she <- 0.3 persp(colahevy)
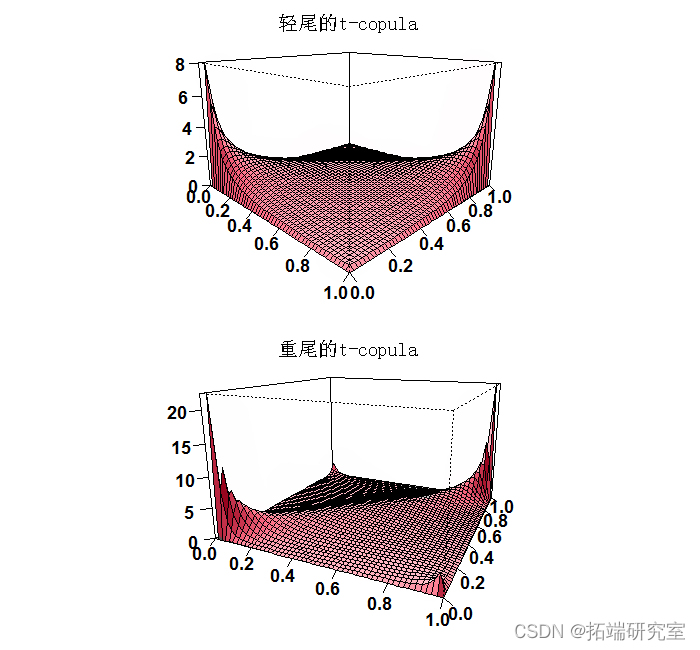
接下来你可以看到通常的相关性度量是相同的，除了尾部指数，因为我们只讨论结构，而不是大小。
tau(colight)
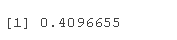
tau(coheavy)
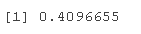
rho(colight)
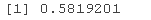
rho(copheavy)
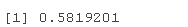
tailIpulight)
tailIheavy)
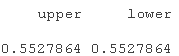
上下尾不一定相同。这只是 t-copula 是对称函数的一个特征。在应用中，应该使用更真实的非对称 copula。
现在我们定义边缘，并估计 copula 参数。为简单起见，我为收益定义了 Normal 边缘分布，但 copula 仍然是 t-dist 且重尾：
# 用从数据中估计的参数来定义你的边际。 copurmal <- mvdc # 拟合copula。这个函数的默认值是隐藏警告，所以如果发生错误。 # 添加 "hideWarnings=FALSE"，这样它就会告诉你是否有什么错误 coporm <- fitMvdc 该函数返回一个有那些可用的S4类。 copurm@mvc@cpla coporm@estiat coporm@fittng.sas coporm@va.st print summary
est <- coeffic # 我们自己的估计值 mycop <- mvdc # 从拟合的copula进行模拟 simd <- rMvdc plot
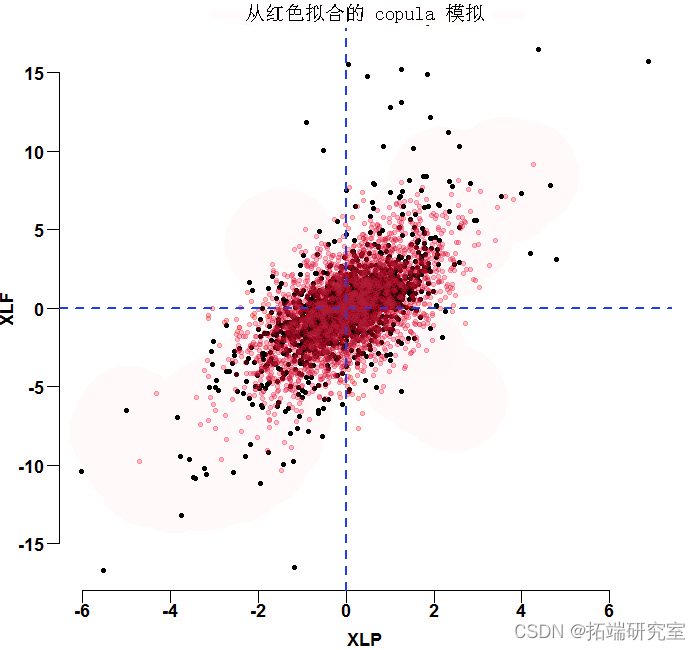
相关结构看起来还不错–但你肯定可以看到正态边缘是不够的，有几个黑点（真实数据）在红色模拟簇之外。
顺便提一下，现在我们也可以估计那些没有预先指定形状的copulas，比如正态或t，但它们本身就是估计。这属于 “非参数copulas “这个更复杂的主题。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python用CNN – LSTM、ARIMA、Prophet股票价格预测的研究与分析|附数据代码
BC变换的EWMA控制图对顺丰控股股票的分析研究
