使用glmnet软件包中的相关函数对岭回归和lasso套索回归进行分析。
拟合岭回归和LASSO回归，解释系数，并对其在λ范围内的变化做一个直观的可视化。
可下载资源
# 加载CBI数据
# 子集所需的变量（又称，列）
CBI_sub <- CBI
# 重命名变量列(节省大量的输入)
names(CBI_sub)\[1\] <- "cbi"
# 只要完整案例，删除缺失值。
CBI\_sub <- CBI\_sub\[complete.cases(CBI_sub),\]
#现在检查一下CBI_sub里面的内容
names(CBI_sub)其实，并没有绝对的好坏。从预测的角度看，如果真实模型（或数据生成过程）确实是稀疏的，则 Lasso 一般表现更优。但如果真实模型并非稀疏，则岭回归可能预测效果优于 Lasso。
另一方面，从模型易于解释（interpretability）的角度，则 Lasso 显然是赢家，因为岭回归一般不具有变量筛选的功能。由于经济学通常强调模型易于解释，故 Lasso 在经济学中的应用更加广泛。
当然，Lasso 在计算上比岭回归略为复杂。由于使用了带绝对值的 1-范数，Lasso 的目标函数并不可微，故不存在解析解。但由于 Lasso 的目标函数仍为凸函数（convex function），故存在很有效率的数值迭代算法（比如，Least Angle Regression，Coordinate Descent Algorithm），在计算上也不是问题。
自从 Lasso 出现以后，学者们脑洞大开，相继提出了一系列有关 Lasso 的推广与变形，以适应不同的研究对象与数据特点，比如 grouped lasso，fused lasso，adaptive lasso，square-root lasso 等。特别值得一提的是 “弹性网估计量”（Elastic Net），它同时将 2-范数与 1-范数引入目标函数的惩罚项，在岭回归与套索估计的性质之间作了折衷，在此不再赘述。
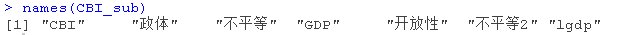
# 设置控制参数
control = method = "cv",number=5) # 5折CV
cbi ~ ., data = CBI_sub, method = "glmnet",
trControl = control, preProc = c("center","scale"), # 中心和标准化数据
# 得到系数估计值（注意，我们真正关心的是β值，而不是S.E.）。
coef(ridge_caret.fit, bestTune$lambda)视频
Lasso回归、岭回归等正则化回归数学原理及R语言实例
视频
什么是Bootstrap自抽样及R语言Bootstrap线性回归预测置信区间
cbi ~ ., data = CBI_sub, method = "glmnet",
tuneGrid = expand.grid(alpha = 1,
# 获得系数估计
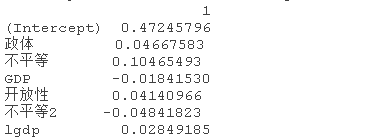
coef(lasso_caret,bestTunelambda)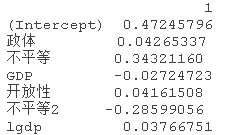
使用glmnet软件包中的相关函数对岭回归和lasso套索回归进行分析。
准备数据
注意系数是以稀疏矩阵格式表示的，因为沿着正则化路径的解往往是稀疏的。使用稀疏格式在时间和空间上更有效率
# 拟合岭回归模型
glmnet(X, Y, alpha = 0)
#检查glmnet模型的输出（注意我们拟合了一个岭回归模型
#记得使用print()函数而不是summary()函数
print(glmnet.fit)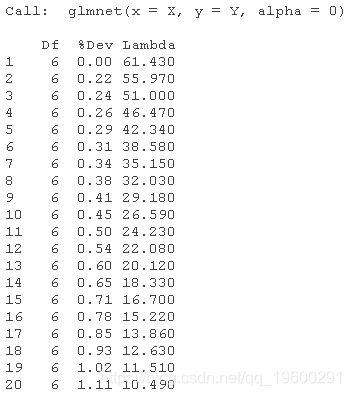
# 输出最佳lamda处的岭回归coefs
coef(glmnet.fit, s = lambda.1se)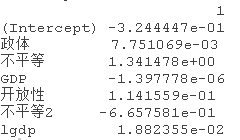
绘制结果
#
plot(ridge_glmnet.fit, label = TRUE)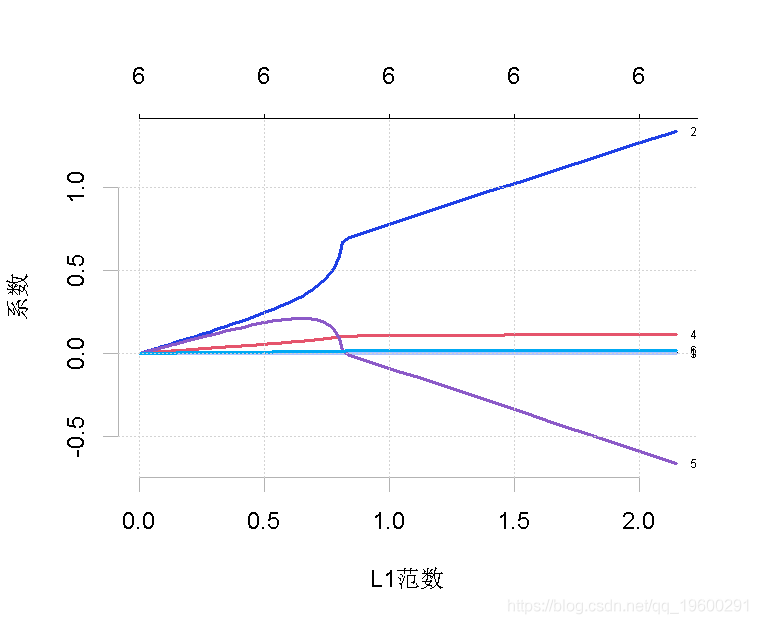
图中显示了随着lambda的变化，模型系数对整个系数向量的L1-norm的路径。上面的轴表示在当前lambda下非零系数的数量，这也是lasso的有效自由度（df）。
par(mfrow=c(1,2)) # 建立1乘2的绘图环境
plot\_glmnet(ridge\_glmnet.fit, xvar = "lambda", label=6, xlab = expression(paste("log(", lambda, ")")), ylab = expression(beta)) # "标签"是指你想让图表显示的前N个变量。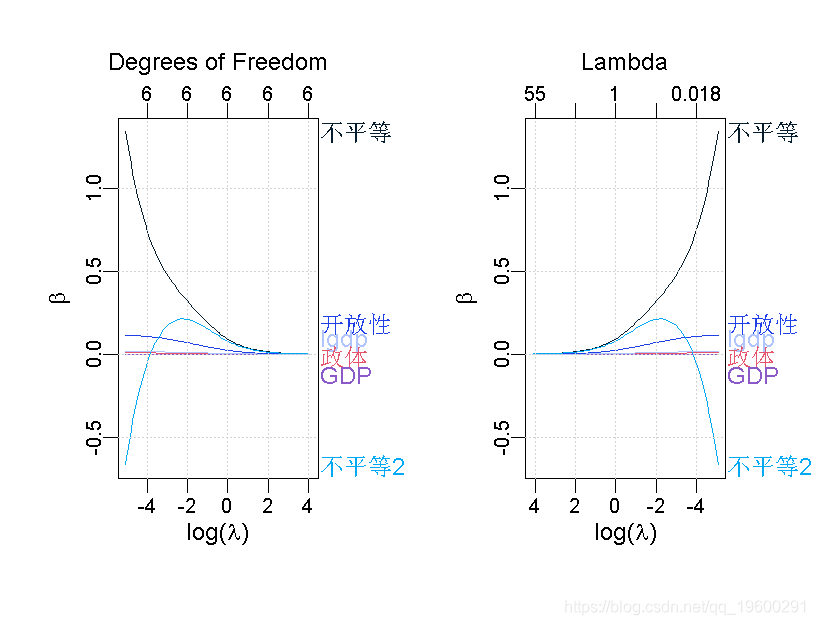
随时关注您喜欢的主题
# 进行变量选择，比如说，我想根据λ>0.1的标准或其他一些值来选择实际系数。
coef(ridge_glmnet.fit, s = 0.1)
交叉验证的岭回归
#
plot(cv.ridge)
# 我们可以查看选定的lambda和相应的系数。例如：
lambda.min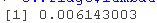
# 根据最小的lambda（惩罚）选择变量
# lambda.min是λ的值，它使交叉验证的平均误差最小
# 选择具有最大惩罚性的一个
coef
## 对lasso模型做同样的处理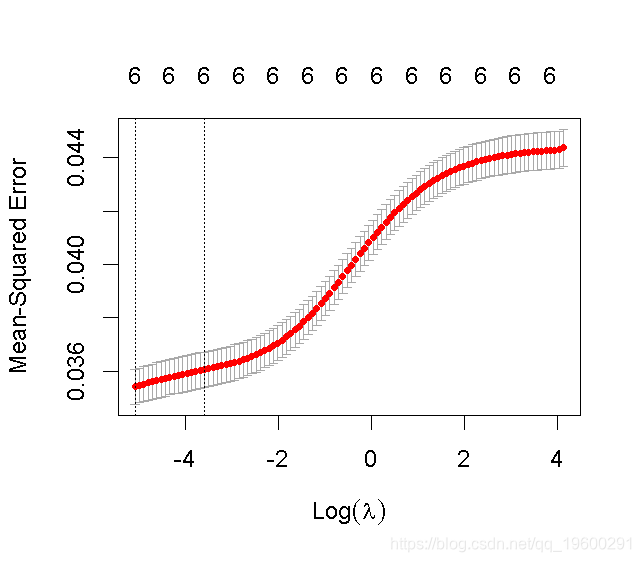
数据挖掘
使用自适应LASSO进行函数形式规范检查
# 加载CBI数据
CBI <- read.csv("dat.csv")
#对需要的变量进行取子集（列）
names(CBI)<- "cbi"fitpoly(degree = 2, thre = 1e-4) # 设置多项式的度数为2
bootstrap
boot(poly.fit1, nboot = 5) #5次bootstrap迭代
交叉验证
# 交叉验证，10折CV
cbi ~ ., data = CBI_sub, degrees.cv = 1:3,)
# 提取最佳模型并进行bootstrap
boot(cv.pred, nboot = 5) # 5次bootstrap
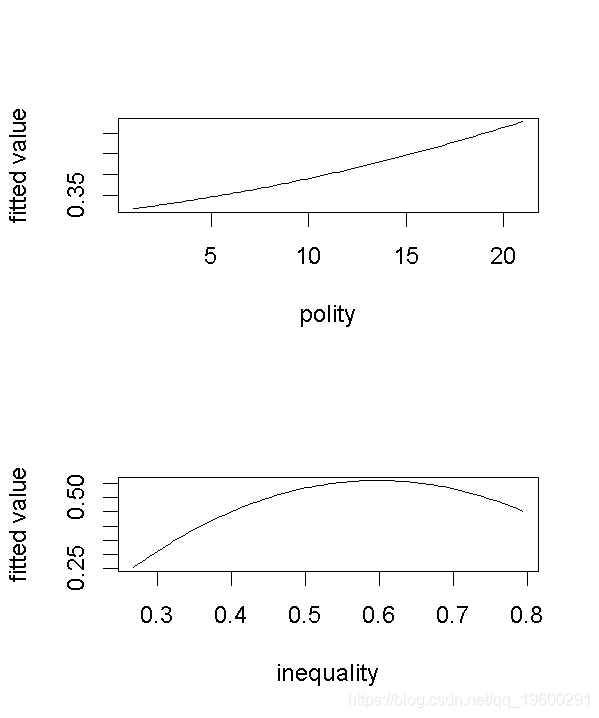
# 绘制cv.boot的预测值的边际效应
marg(cv.boot))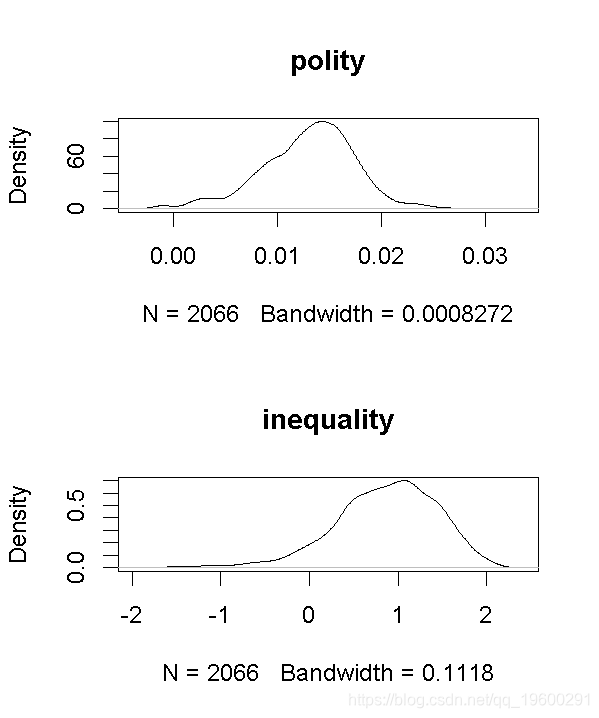
补充
获得岭回归和LASSO模型的bootstrap平均数
#如果你想要S.E.，通过bootstrap模拟得到它。
library(boot)
boot(CBI_sub, function(data, idx)
bootSamples可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言混合模型回归GBTM群组轨迹模型绘图可视化研究
Python深度强化学习智能体DDPG自适应股票交易策略优化道琼斯30股票数据可视化研究
Python、R语言Lasso、Ridge岭回归、XGBoost分析Airbnb房屋数据：旅游市场差异、价格预测
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
