在这个例子中,我们考虑随机波动率模型 SV0 的应用,例如在金融领域。
最近我们被客户要求撰写关于随机波动率(SV)的研究报告,包括一些图形和统计输出。
在金融市场的研究与实践中,准确预测资产价格波动是投资者和金融分析师追求的重要目标。
标准普尔 500 指数(S&P 500)作为反映美国股市整体表现的重要指标,其波动特性的分析与预测一直备受关注。
随机波动率(Stochastic Volatility,SV)模型和马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法中的 Metropolis-Hastings 算法,为研究金融时间序列的波动提供了强大的工具。
本文将深入探讨如何运用 R 语言,结合 SV 模型与 Metropolis-Hastings 算法,对标准普尔 500 指数进行预测分析。
随机波动率模型定义如下
统计模型

很多人用贝叶斯统计Mcmc方法估计主要是因为与GARCH 类模型相比,SV 类模型的参数估计要复杂和困难得多。由于在SV模型中波动率过程是潜藏的,不能够被直接观察。因此,在估计参数每一步骤中务必处理好潜在变量,处理潜在变量常使用的方法有寻找替代变量或者在似然函数中通过用积分的方法将潜在变量消去,这两种方法对于SV 模型都不适用。正是由于这些原因,常见的参数估计方法很难对SV 模型中的参数进行估计。
在sv模型中,需要对序列内所有对数隐含波动进行积分,公式如下:
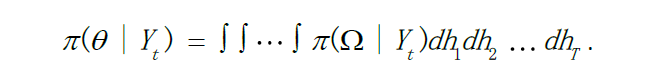
h是潜在波动率,t是样本观测量,这样积分计算量非常的大边缘后验分布密度分布和似然函数是一个高维积分过程,因为计算复杂,不适合用极大似然估计方法进行参数估计。然而在基于贝叶斯的MCMC 抽样算法框架下,未知参数和对数隐含波动向量的联合后验分布可以直接通过Gibbs 抽样方法进行估计,也就是将参数空间扩展为一个包含对数隐含波动向量在内的新的参数空间,从而将问题转化成从完全条件后验分布中抽取随机样本。
关于参数的先验分布和初始值
根据WinBUGS User Manual,给出的解释是

先验值的设立影响到后续的迭代,最好根据所参考文献推荐的先验值进行设立,随机生成的先验值可能回生成极端值从而影响迭代。
根据R语言stochvol包,给出的建议是:

而根据
Jun Yu, Renate Meyer. Multivariate Stochastic Volatility Models: Bayesian Estimation and Model Comparison[J]. Econometric Reviews, 2006, 25(2-3):24.
这篇论文,多元随机波动率模型先验参数设立为

总之,先验值的设立影响到后续的迭代,最好根据所参考文献推荐的先验值进行设立,随机生成的先验值可能回生成极端值从而影响迭代。
并为


其中 yt 是因变量,xt 是 yt 的未观察到的对数波动率。N(m,σ2) 表示均值 m 和方差 σ2 的正态分布。
αα、β 和 σ 是需要估计的未知参数。
BUGS语言统计模型
文件内容 'sv.bug':
moelfle = 'sv.bug' # BUGS模型文件名 cat(readLies(moelfle ), sep = "\\n")
# 随机波动率模型SV_0
# 用于随机波动率模型
var y\[t\_max\], x\[t\_max\], prec\_y\[t\_max\]
model
{
alha ~ dnorm(0,10000)
logteta ~ dnorm(0,.1)
bea <- ilogit(loit_ta)
lg_sima ~ dnorm(0, 1)
sia <- exp(log_sigma)
x\[1\] ~ dnorm(0, 1/sma^2)
pr_y\[1\] <- exp(-x\[1\])
y\[1\] ~ dnorm(0, prec_y\[1\])
for (t in 2:t_max)
{
x\[t\] ~ dnorm(aa + eta*(t-1\]-alha, 1/ia^2)
pr_y\[t\] <- exp(-x\[t\])
y\[t\] ~ dnorm(0, prec_y\[t\])
}
设置
设置随机数生成器种子以实现可重复性
set.seed(0)
加载模型并加载或模拟数据
sample_data = TRUE # 模拟数据或SP500数据
t_max = 100
if (!sampe_ata) {
# 加载数据 tab = read.csv('SP500.csv')
y = diff(log(rev(tab$ose)))
SP5ate_str = revtab$te\[-1\])
ind = 1:t_max
y = y\[ind\]
SP500\_dae\_r = SP0dae_tr\[ind\]
SP500\_e\_num = as.Date(SP500_dtetr)
模型参数
if (!smle_dta) {
dat = list(t_ma=ax, y=y)
} else {
sigrue = .4; alpa_rue = 0; bettrue=.99;
dat = list(t\_mx=\_mx, sigm_tue=simarue,
alpatrue=alhatrue, bet\_tue=e\_true)
}
如果模拟数据,编译BUGS模型和样本数据

data = mdl$da()
绘制数据


对数收益率
Biips粒子边际Metropolis-Hastings
我们现在运行Biips粒子边际Metropolis-Hastings (Particle Marginal Metropolis-Hastings),以获得参数 α、β 和 σ 以及变量 x 的后验 MCMC 样本。
PMMH的参数
n_brn = 5000 # 预烧/适应迭代的数量
n_ir = 10000 #预烧后的迭代次数
thn = 5 #对MCMC输出进行稀释
n_art = 50 # 用于SMC的nb个粒子
para\_nmes = c('apha', 'loit\_bta', 'logsgma') # 用MCMC更新的变量名称(其他变量用SMC更新)。
latetnams = c('x') # 用SMC更新的、需要监测的变量名称
初始化PMMH

运行 PMMH
update(b\_pmh, n\_bun, _rt) #预烧和拟合迭代
随时关注您喜欢的主题

samples(oj\_mh, ter, n\_art, thin=hn) # 采样

汇总统计
summary(otmmh, prob=c(.025, .975))
计算核密度估计
density(out_mh)
参数的后验均值和置信区间
for (k in 1:length(pram_names)) {
suparam = su\_pmm\[\[pam\_as\[k\]\]\]
cat(param$q)
}

参数的MCMC样本的踪迹
if (amldata)
para\_tue = c(lp\_tue, log(dt$bea_rue/(-dta$eatru)), log(smtue))
)
for (k in 1:length(param_aes)) {
smps_pm = tmmh\[\[paranesk\]\]
plot(samlespram\[1,\]

PMMH:跟踪样本参数
参数后验的直方图和 KDE 估计
for (k in 1:length(paramns)) {
samps\_aram = out\_mmh\[\[pramnaes\[k\]\]\]
hist(sple_param)
if (sample_data)
points(parm_true)
}
PMMH:直方图后验参数

for (k in 1:length(parm) {
kd\_pram =kde\_mm\[\[paramames\[k\]\]\]
plot(kd_arm, col'blue
if (smpldata)
points(ar_true\[k\])
}

PMMH:KDE 估计后验参数
x 的后均值和分位数
x\_m\_mean = x$mean
x\_p\_quant =x$quant
plot(xx, yy)
polygon(xx, yy)
lines(1:t\_max, x\_p_man)
if (ame_at) {
lines(1:t\_ax, x\_true)
} else
legend(
bt='n)

PMMH:后验均值和分位数
x 的 MCMC 样本的踪迹
par(mfrow=c(2,2))
for (k in 1:length) {
tk = ie_inex\[k\]
if (sample_data)
points(0, dtax_t
}
if (sml_aa) {
plot(0
legend('center')
}

PMMH:跟踪样本 x
x 后验的直方图和核密度估计
par(mfow=c(2,2))
for (k in 1:length(tie_dex)) {
tk = tmnex\[k\]
hist(ot_m$x\[tk,\]
main=aste(t=', t, se='')
if (sample_data)
points(ata$x_re\[t\],
}
if (saml_dta) {
plot(0, type='n', bty='n', x
legend('center
bty='n')
}

PMMH:后_边际_直方图
par(mfrow=c(2,2))
for (k in 1:length(idx)) {
tk =m_dx\[k\]
plot(kmmk\]\] if (alata)
point(dat_r\[k\], 0)
}
if (aldt) {
plot(0, type='n', bty='n', x, pt.bg=c(4,NA)')
}


可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
专题:Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据 【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用
【视频讲解】R语言海七鳃鳗性别比分析:JAGS贝叶斯分层逻辑回归MCMC采样模型应用 专题|Python贝叶斯金融数据应用实例合集:随机波动率SV模型、逻辑回归、参数更新、绩效比较BEST分析亚马逊股票、标准普尔500指数|附数据代码
专题|Python贝叶斯金融数据应用实例合集:随机波动率SV模型、逻辑回归、参数更新、绩效比较BEST分析亚马逊股票、标准普尔500指数|附数据代码 Python用PyMC3马尔可夫链蒙特卡罗MCMC对疾病症状数据贝叶斯推断
Python用PyMC3马尔可夫链蒙特卡罗MCMC对疾病症状数据贝叶斯推断



