在这里，我们放宽了流行的线性方法的假设。有时线性假设只是一个很差的近似值。
视频
非线性模型原理与R语言多项式回归、局部平滑样条、 广义相加模型GAM分析
总览
本文本专注于线性模型的扩展
- 多项式回归 这是对数据提供非线性拟合的简单方法。
- 阶跃函数 将变量的范围划分为 K个 不同的区域，以生成定性变量。这具有拟合分段常数函数的效果。
- 回归样条 比多项式和阶跃函数更灵活，并且实际上是两者的扩展。
- 局部样条曲线 类似于回归样条曲线，但是允许区域重叠，并且可以平滑地重叠。
- 平滑样条曲线 也类似于回归样条曲线，但是它们最小化平滑度惩罚的残差平方和准则 。
- 广义加性模型 允许扩展上述方法以处理多个预测变量。
在实际应用中，我们常常对总体进行某种分布的假设，抽样得到样本信息，去估计总体参数，这种方法称为参数估计方法。但当对总体信息一无所知，或不假定总体分布形式，只通过样本信息对总体参数进行估计，此时，非参数估计就展现了很强的灵活性。
非参数回归分为局部回归、光滑样条回归、正交回归。光滑样条回归，因其在抽取样本对总体进行回归时，不必依赖总体分布形式，在减小误差、提高预测精确度、提高拟合曲线的光滑度上都体现了良好的特性。
非参数回归模型的一般形式及模型
设Y为因变量 X1,X2,⋯,Xp 为自变量，非参数回归模型的一般形式为
Y=η(X1,X2,⋯,Xp)+ε
其中对p元回归函数只作一些连续性或光滑性的要求。由于非参数回归模型不假定回归函的具体形式而增加了模型的灵活性和适应性。
设 (yi,xi) Math_12#为来自总体 (Y,X) 的一个样本容量为n的独立同分布的样本，需要基于观测值 (yi,xi) Math_15#估计 η(x) 并进行有关的统计推断。
非参数回归的模型为:
E(Y|X=x)=g(X)
数据和模型是统计分析的两个信息来源，数据带有“噪声”，但无偏，而模型实际上是种约束，有助于降低噪声，是响应的。在“偏差–方差”的平衡表上，代表两个极值的分别是标准参数模型和无约束非参数模型。在两个极值之间，存在着大量的非参数或半参数模型，其中大多数被称为平滑方法。非参数估计族可通过惩罚似然法导出各种随机环境下的模型。
多项式回归
这是扩展线性模型的最传统方法。随着我们增加 多项式的项，多项式回归使我们能够生成非线性的曲线，同时仍使用最小二乘法估计系数。
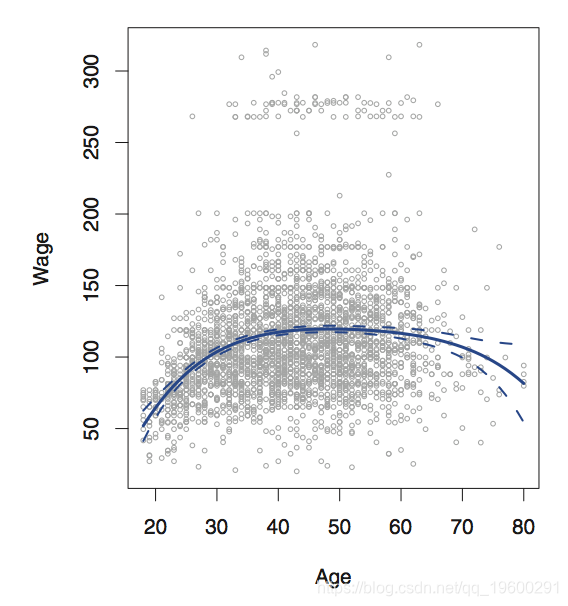
逐步回归
它经常用于生物统计学和流行病学中。
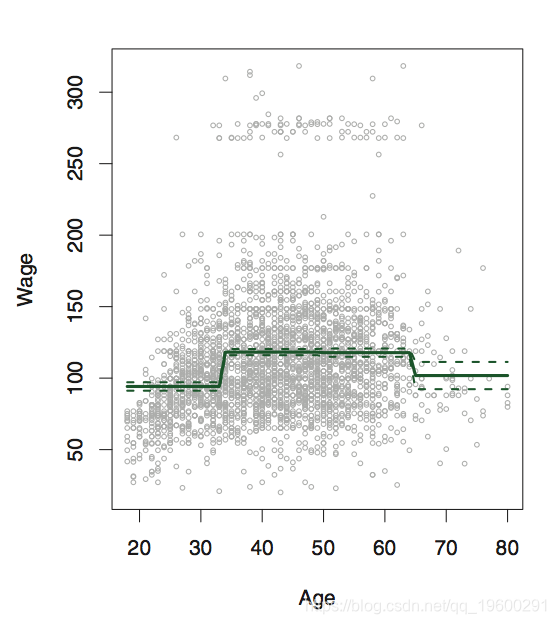
回归样条
回归样条是 扩展多项式和逐步回归技术的许多基本函数之一 。事实上。多项式和逐步回归函数只是基 函数的特定情况 。
这是分段三次拟合的示例（左上图）。
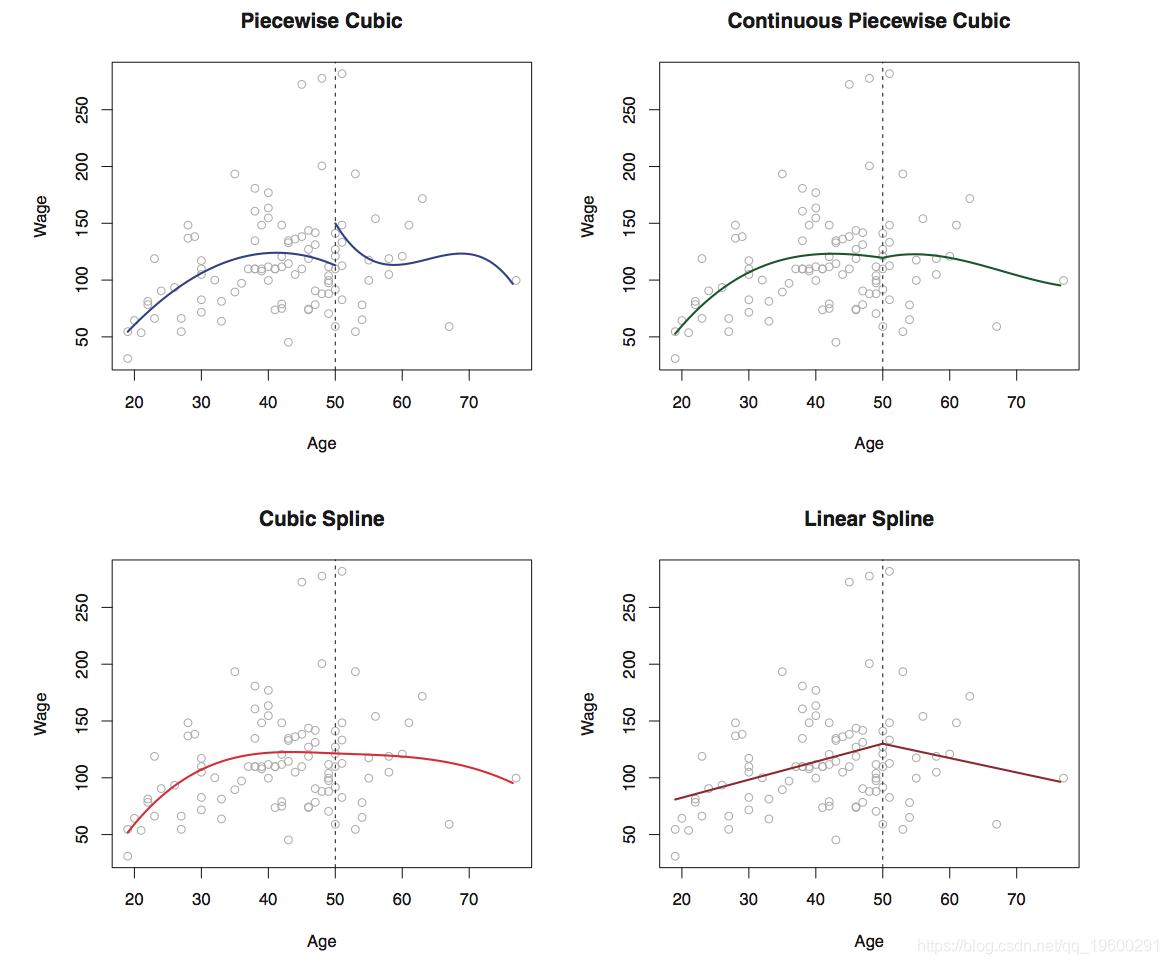
为了解决此问题，更好的解决方案是采用约束，使拟合曲线必须连续。
选择结的位置和数量
一种选择是在我们认为变化最快的地方放置更多的结，而在更稳定的地方放置更少的结。但是在实践中，通常以统一的方式放置结。
要清楚的是，在这种情况下，实际上有5个结，包括边界结。
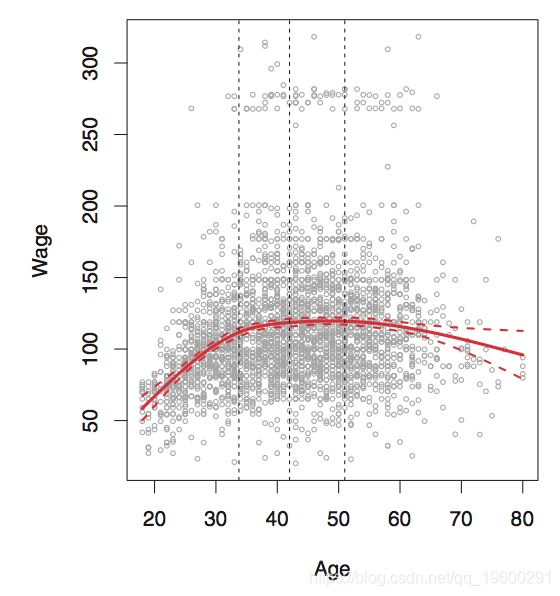
那么我们应该使用多少个结？一个简单的选择是尝试许多个结，然后看哪个会产生最好的曲线。但是，更客观的方法是使用交叉验证。
与多项式回归相比，样条曲线可以显示出更稳定的效果。
平滑样条线
我们讨论了回归样条曲线，该样条曲线是通过指定一组结，生成一系列基函数，然后使用最小二乘法估计样条系数而创建的。平滑样条曲线是创建样条曲线的另一种方法。让我们回想一下，我们的目标是找到一些非常适合观察到的数据的函数，即最大限度地减少RSS。但是，如果对我们的函数没有任何限制，我们可以通过选择精确内插所有数据的函数来使RSS设为零。
选择平滑参数Lambda
同样，我们求助于交叉验证。事实证明，我们实际上可以非常有效地计算LOOCV，以平滑样条曲线，回归样条曲线和其他任意基函数。
平滑样条线通常比回归样条线更可取，因为它们通常会创建更简单的模型并具有可比的拟合度。
局部回归
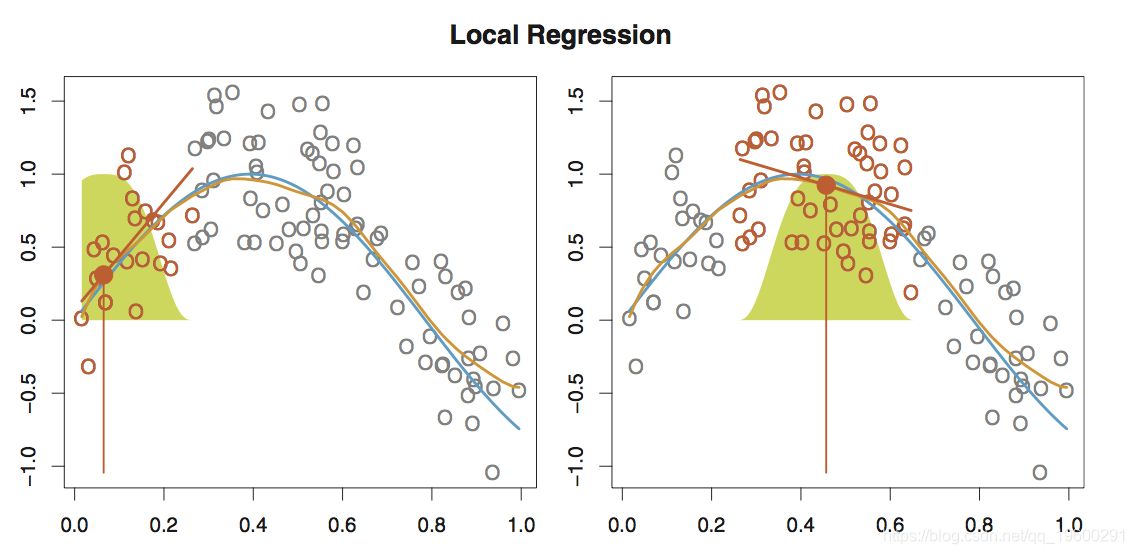
局部回归涉及仅使用附近的训练观测值来计算目标点x 0 处的拟合度 。
可以通过各种方式执行局部回归，尤其是在涉及拟合_p_ 线性回归模型的多变量方案中尤为明显 ，因此某些变量可以全局拟合，而某些局部拟合。
广义相加（加性）模型
GAM模型提供了一个通用框架，可通过允许每个变量的非线性函数扩展线性模型，同时保持可加性。
具有平滑样条的GAM并不是那么简单，因为不能使用最小二乘。取而代之的 是使用一种称为_反向拟合_的方法 。
GAM的优缺点
优点
- GAM允许将非线性函数拟合到每个预测变量，以便我们可以自动对标准线性回归会遗漏的非线性关系进行建模。我们不需要对每个变量分别尝试许多不同的转换。
- 非线性拟合可以潜在地对因变量_Y_做出更准确的预测 。
- 因为模型是可加的，所以我们仍然可以检查每个预测变量对_Y_的影响， 同时保持其他变量不变。
缺点
- 主要局限性在于该模型仅限于累加模型，因此可能会错过重要的交互作用。
范例
多项式回归和阶跃函数
library(ISLR)
attach(Wage)我们可以轻松地使用来拟合多项式函数，然后指定多项式的变量和次数。该函数返回正交多项式的矩阵，这意味着每列是变量的变量的线性组合 age， age^2， age^3，和 age^4。
如果要直接获取变量，可以指定 raw=TRUE，但这不会影响预测结果。它可用于检查所需的系数估计。
fit = lm(wage~poly(age, 4), data=Wage)
kable(coef(summary(fit)))
现在让我们创建一个ages 我们要预测的向量。最后，我们将要绘制数据和拟合的4次多项式。
ageLims <- range(age)
age.grid <- seq(from=ageLims[1], to=ageLims[2])
pred <- predict(fit, newdata = list(age = age.grid),
se=TRUE) plot(age,wage,xlim=ageLims ,cex=.5,col="darkgrey")
lines(age.grid,pred$fit,lwd=2,col="blue")
matlines(age.grid,se.bands,lwd=2,col="blue",lty=3)随时关注您喜欢的主题
在这个简单的示例中，我们可以使用ANOVA检验 。
数据集包含159571条记录
## Analysis of Variance Table
##
## Model 1: wage ~ age
## Model 2: wage ~ poly(age, 2)
## Model 3: wage ~ poly(age, 3)
## Model 4: wage ~ poly(age, 4)
## Model 5: wage ~ poly(age, 5)
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 2998 5022216
## 2 2997 4793430 1 228786 143.59 <2e-16 ***
## 3 2996 4777674 1 15756 9.89 0.0017 **
## 4 2995 4771604 1 6070 3.81 0.0510 .
## 5 2994 4770322 1 1283 0.80 0.3697
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 我们看到，_M_1 与二次模型 相比，p值 _M_2 实质上为零，这表明线性拟合是不够的。 因此，我们可以得出结论，二次方或三次模型可能更适合于此数据，并且偏向于简单模型。
我们也可以使用交叉验证来选择多项式次数。
在这里，我们实际上看到的最小交叉验证误差是针对4次多项式的，但是选择3次或2次模型并不会造成太大损失。接下来，我们考虑预测个人是否每年收入超过25万。
但是，概率的置信区间是不合理的，因为我们最终得到了一些负概率。为了生成置信区间，更有意义的是转换对 数 预测。
绘制：
plot(age,I(wage>250),xlim=ageLims ,type="n",ylim=c(0,.2))
lines(age.grid,pfit,lwd=2, col="blue")
matlines(age.grid,se.bands,lwd=1,col="blue",lty=3)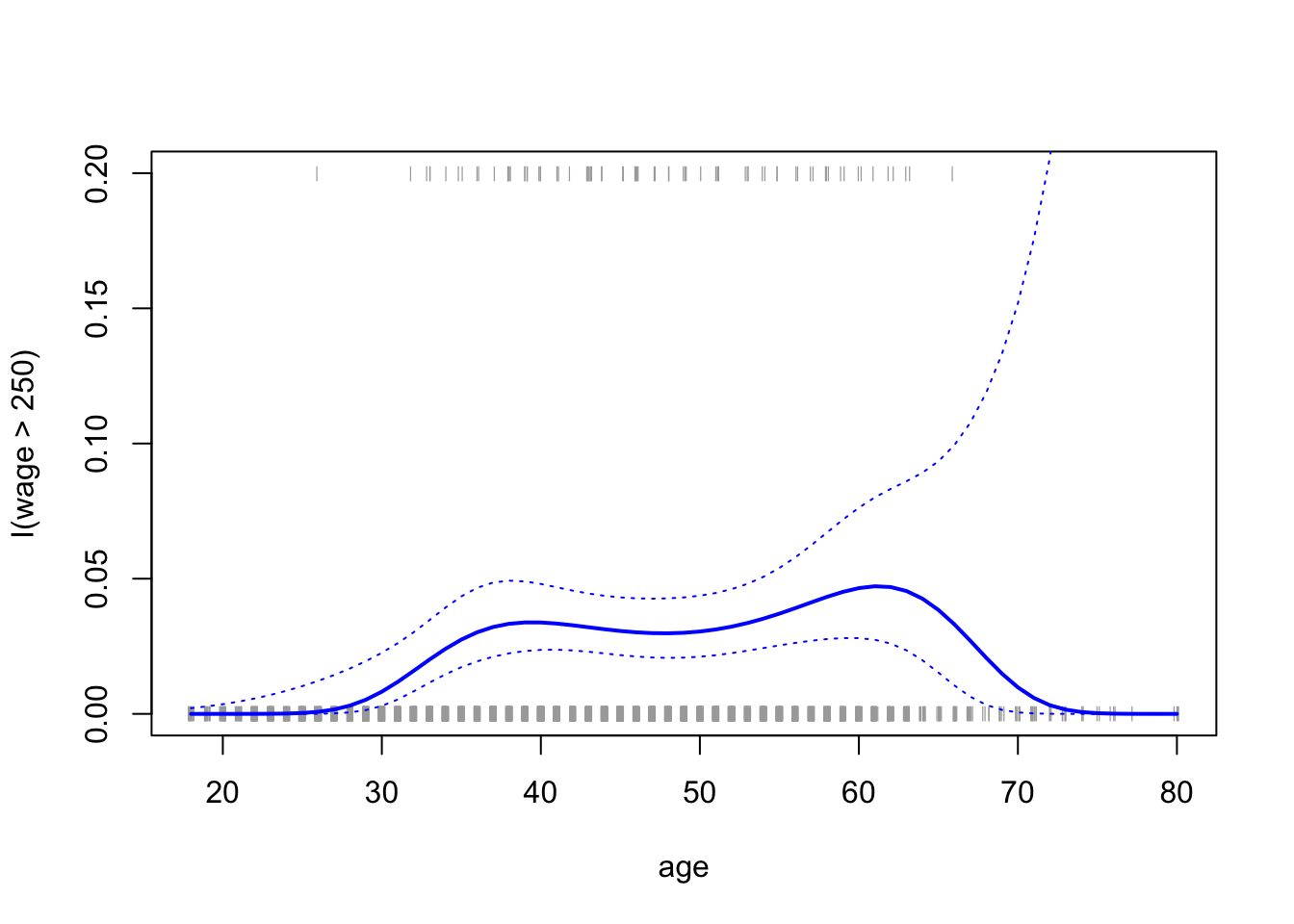
逐步回归函数
在这里，我们需要拆分数据。
table(cut(age, 4)) ##
## (17.9,33.5] (33.5,49] (49,64.5] (64.5,80.1]
## 750 1399 779 72fit <- lm(wage~cut(age, 4), data=Wage)
coef(summary(fit))## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 94.158 1.476 63.790 0.000e+00
## cut(age, 4)(33.5,49] 24.053 1.829 13.148 1.982e-38
## cut(age, 4)(49,64.5] 23.665 2.068 11.443 1.041e-29
## cut(age, 4)(64.5,80.1] 7.641 4.987 1.532 1.256e-01splines 样条函数
在这里，我们将使用三次样条。
当我们与子组的
## [1] 3000 6
dim(bs(age, df=6))
## [1] 3000 6
## 25% 50% 75%
## 33.75 42.00 51.00 由于我们使用的是三个结的三次样条，因此生成的样条具有六个基函数。交易量和价格通常作为单独的数据对象提供。对于许多与交易数据有关的研究和实际问题，需要合并交易量和价格。
拟合样条曲线。
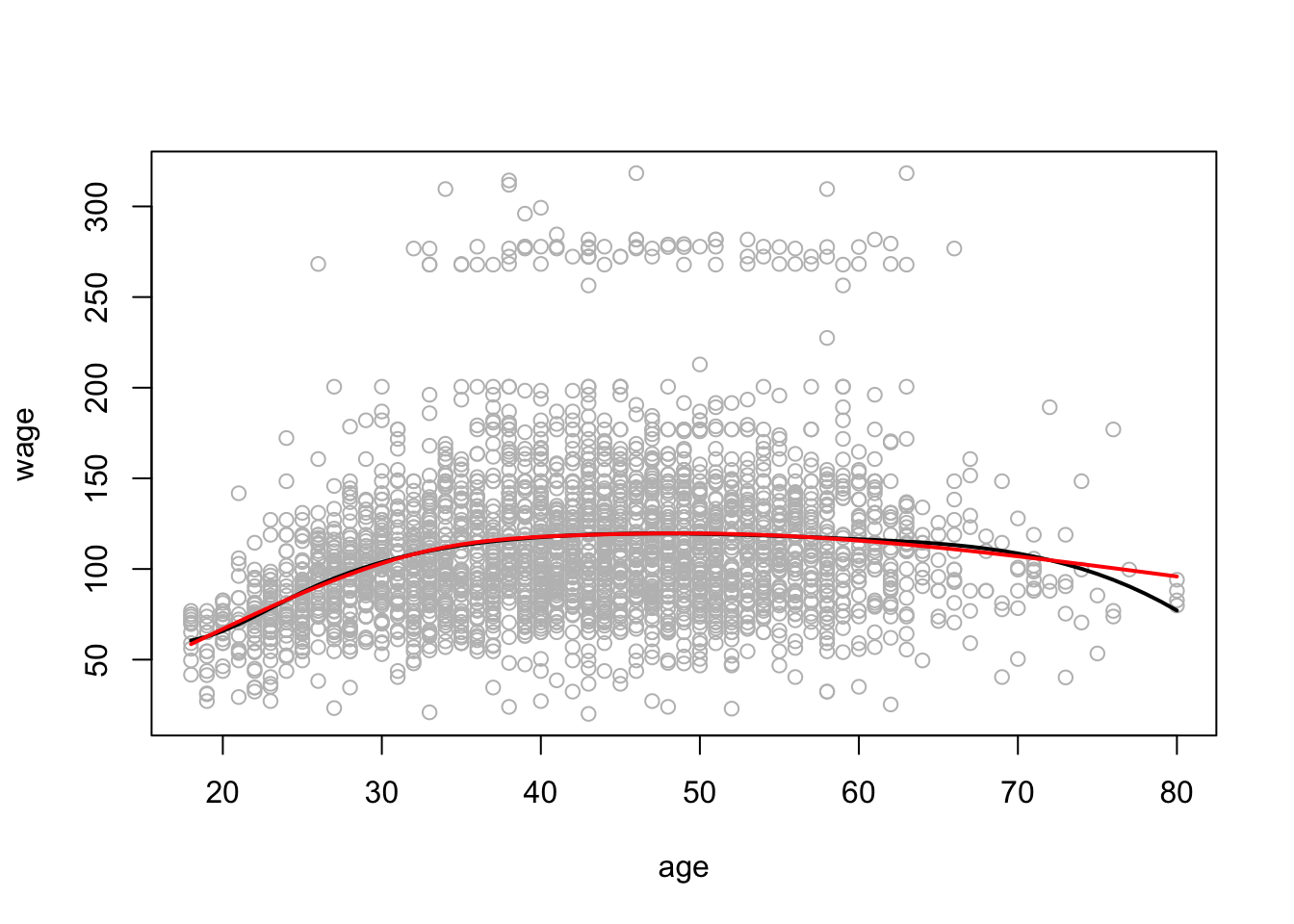
我们也可以拟合平滑样条。在这里，我们拟合具有16个自由度的样条曲线，然后通过交叉验证选择样条曲线，从而产生6.8个自由度。
fit2$df
## [1] 6.795
lines(fit, col='red', lwd=2)
lines(fit2, col='blue', lwd=1)
legend('topright', legend=c('16 DF', '6.8 DF'),
col=c('red','blue'), lty=1, lwd=2, cex=0.8)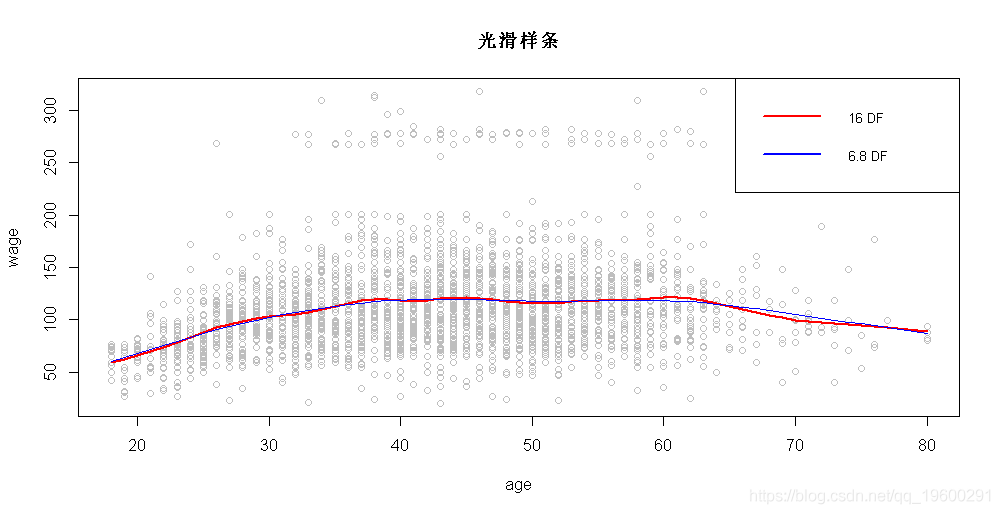 
局部回归
执行局部回归。
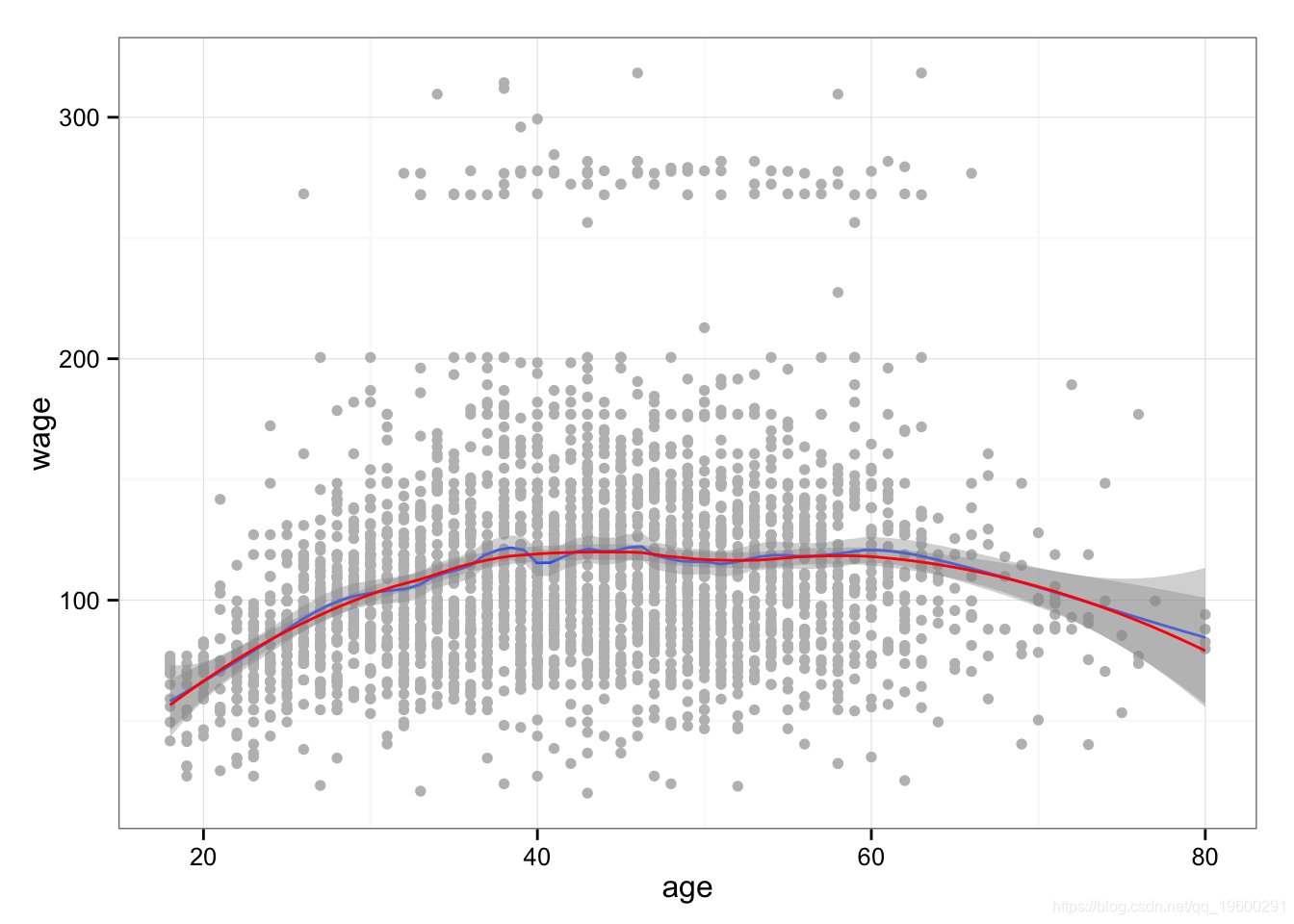
为了拟合更复杂的样条曲线 ，我们需要使用平滑样条曲线。
GAMs
现在，我们使用GAM通过年份，年龄和受教育程度的样条来预测工资。由于这只是具有多个基本函数的线性回归模型，因此我们仅使用 lm() 函数。
绘制这两个模型
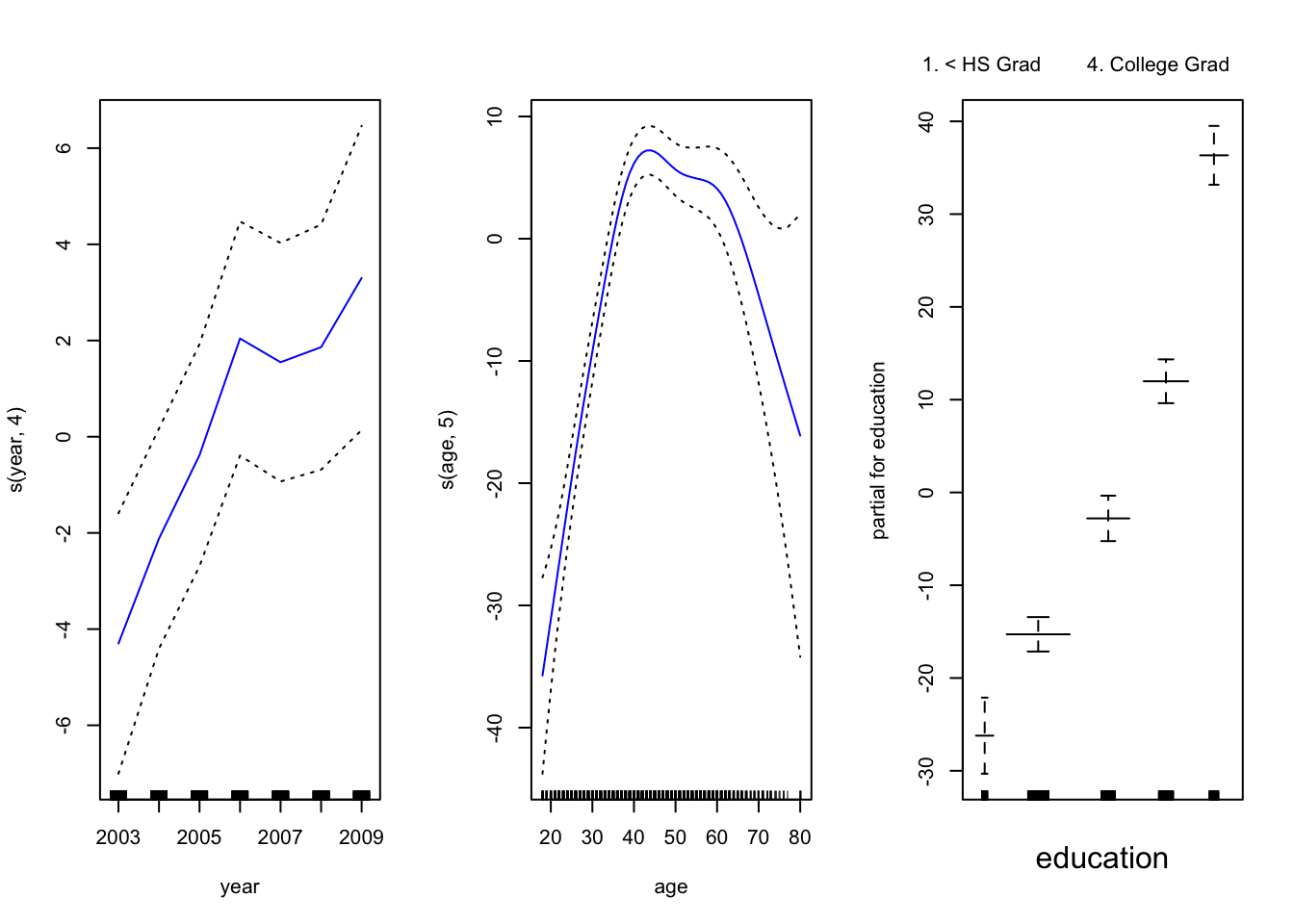
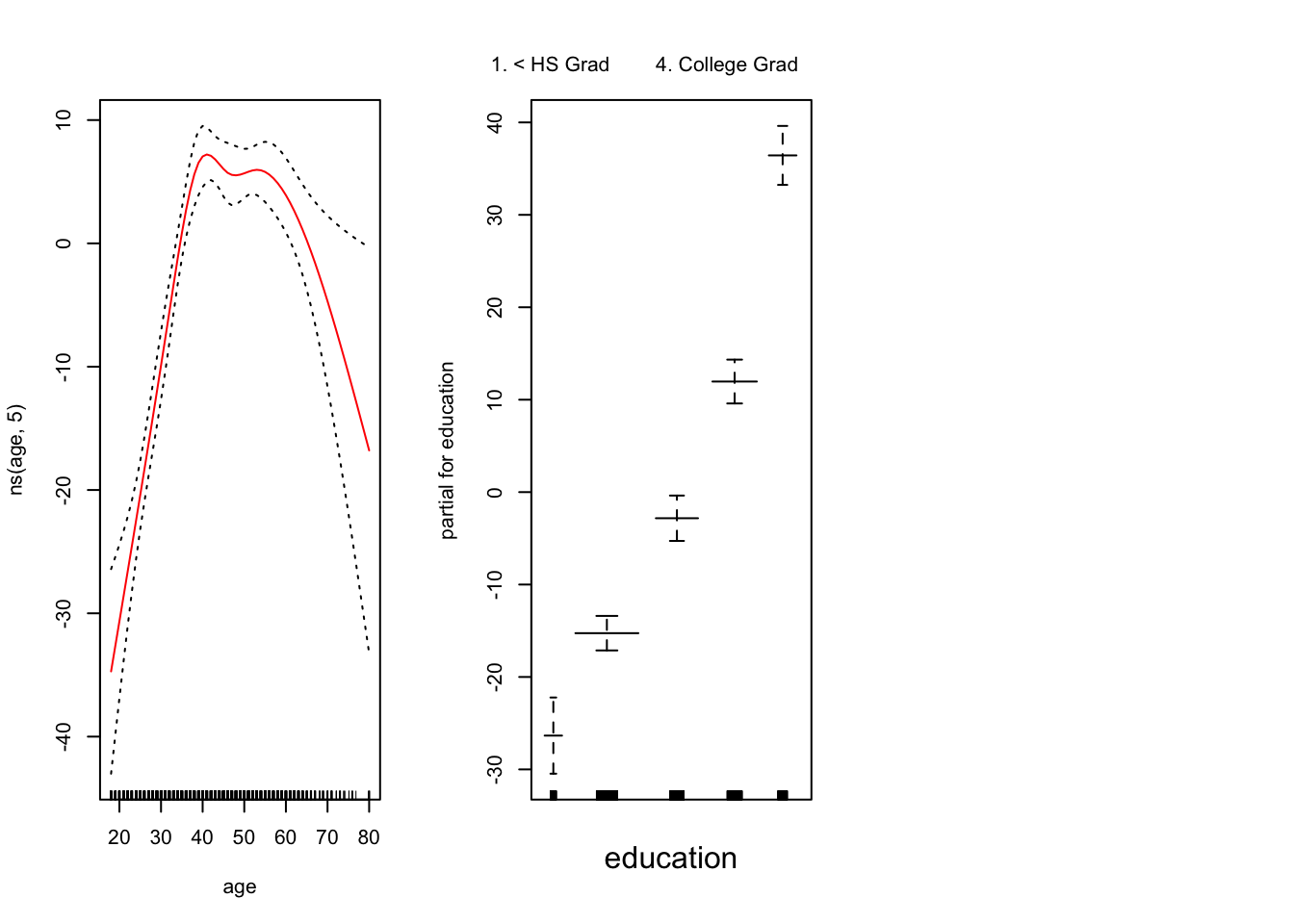
year 是线性的。我们可以创建一个新模型，然后使用ANOVA检验 。
## Analysis of Variance Table
##
## Model 1: wage ~ ns(age, 5) + education
## Model 2: wage ~ year + s(age, 5) + education
## Model 3: wage ~ s(year, 4) + s(age, 5) + education
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 2990 3712881
## 2 2989 3693842 1 19040 15.4 8.9e-05 ***
## 3 2986 3689770 3 4071 1.1 0.35
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 似乎添加线性year 成分要比不添加线性 成分的GAM好得多。
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -119.43 -19.70 -3.33 14.17 213.48
##
## (Dispersion Parameter for gaussian family taken to be 1236)
##
## Null Deviance: 5222086 on 2999 degrees of freedom
## Residual Deviance: 3689770 on 2986 degrees of freedom
## AIC: 29888
##
## Number of Local Scoring Iterations: 2
##
## Anova for Parametric Effects
## Df Sum Sq Mean Sq F value Pr(>F)
## s(year, 4) 1 27162 27162 22 2.9e-06 ***
## s(age, 5) 1 195338 195338 158 < 2e-16 ***
## education 4 1069726 267432 216 < 2e-16 ***
## Residuals 2986 3689770 1236
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Anova for Nonparametric Effects
## Npar Df Npar F Pr(F)
## (Intercept)
## s(year, 4) 3 1.1 0.35
## s(age, 5) 4 32.4 <2e-16 ***
## education
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 在具有非线性关系的模型中， 我们可以再次确认year 对模型没有贡献。
接下来，我们 将局部回归拟合GAM 。
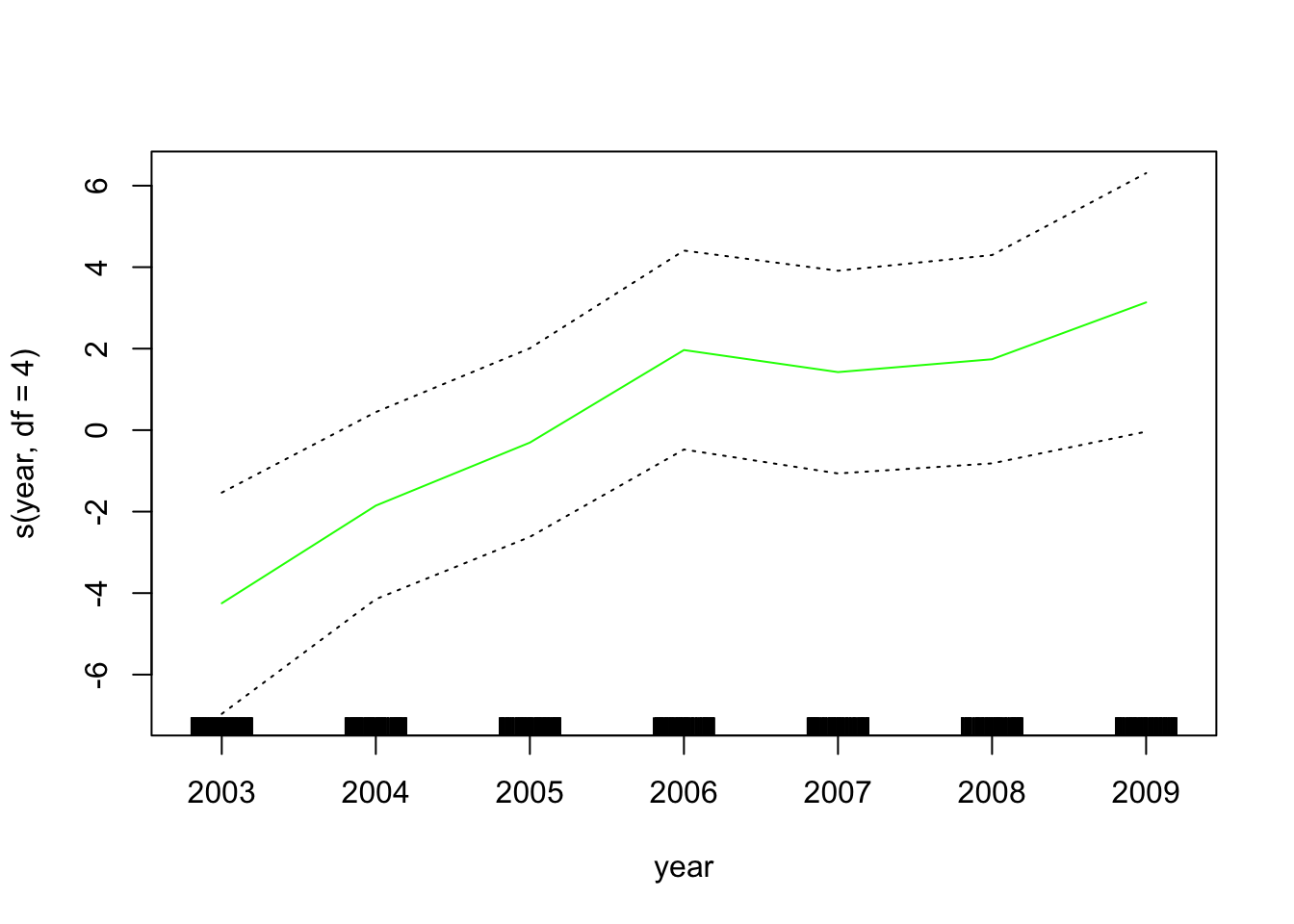
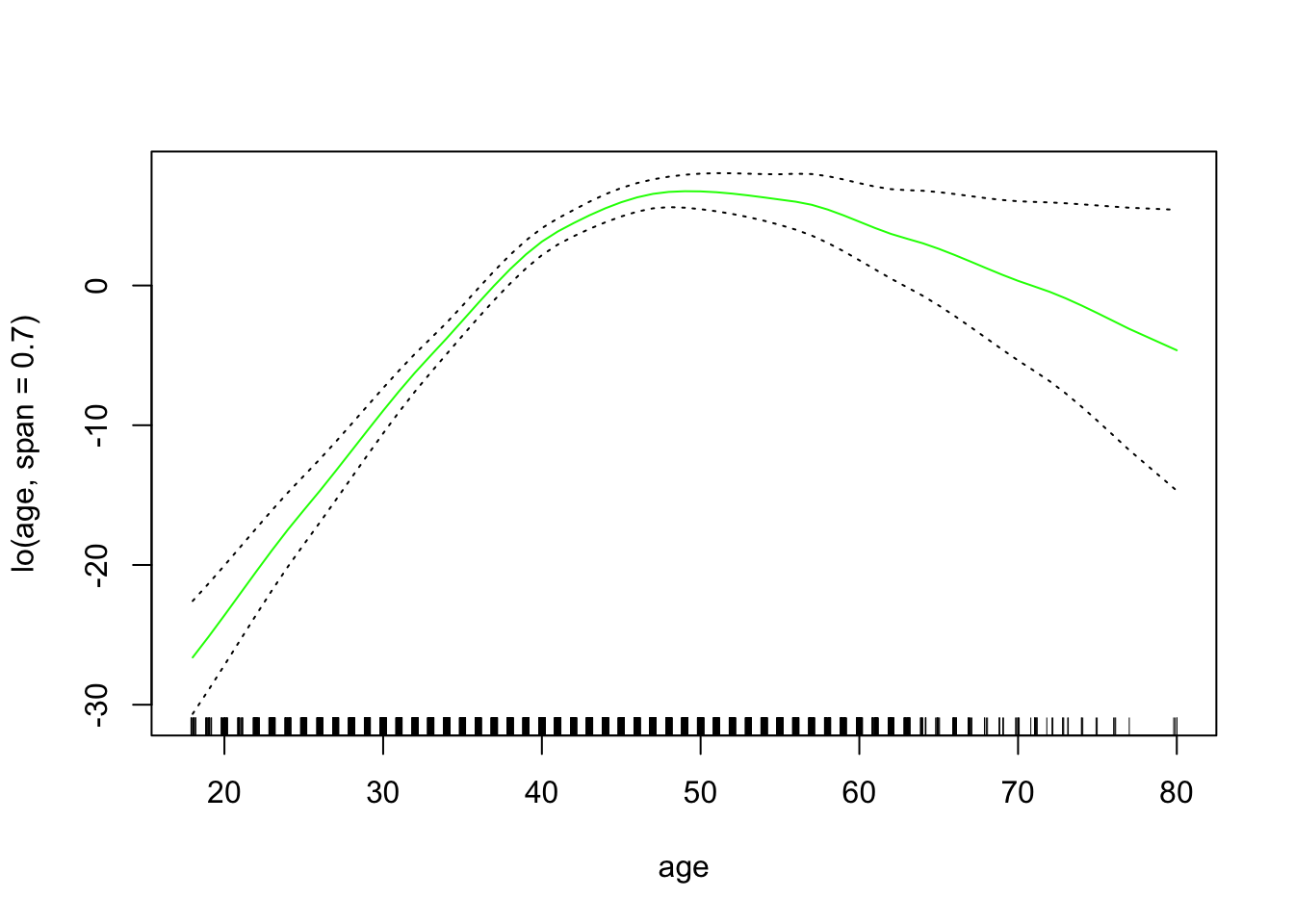
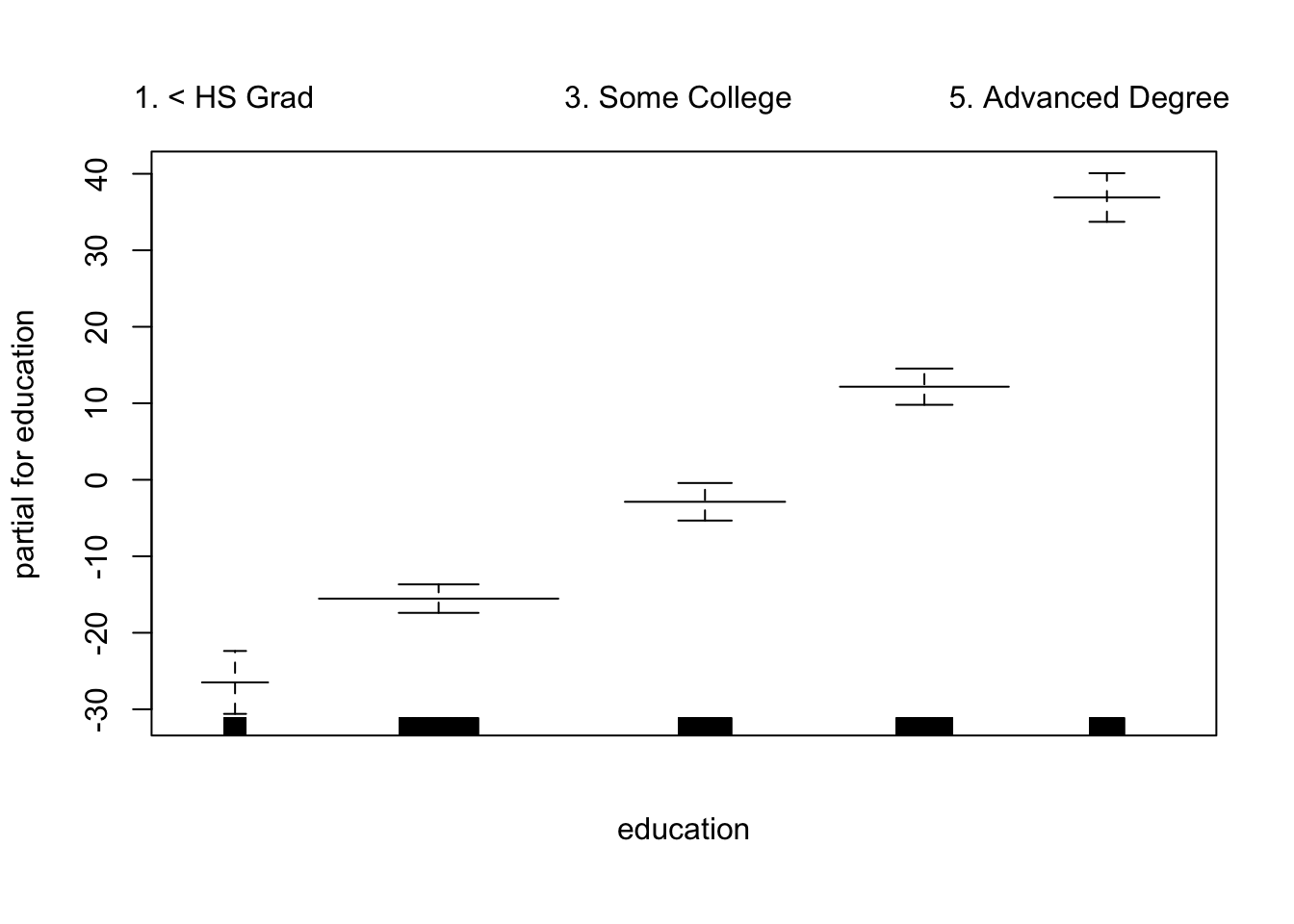
在调用GAM之前，我们还可以使用局部回归来创建交互项。
我们可以 绘制结果曲面图 。
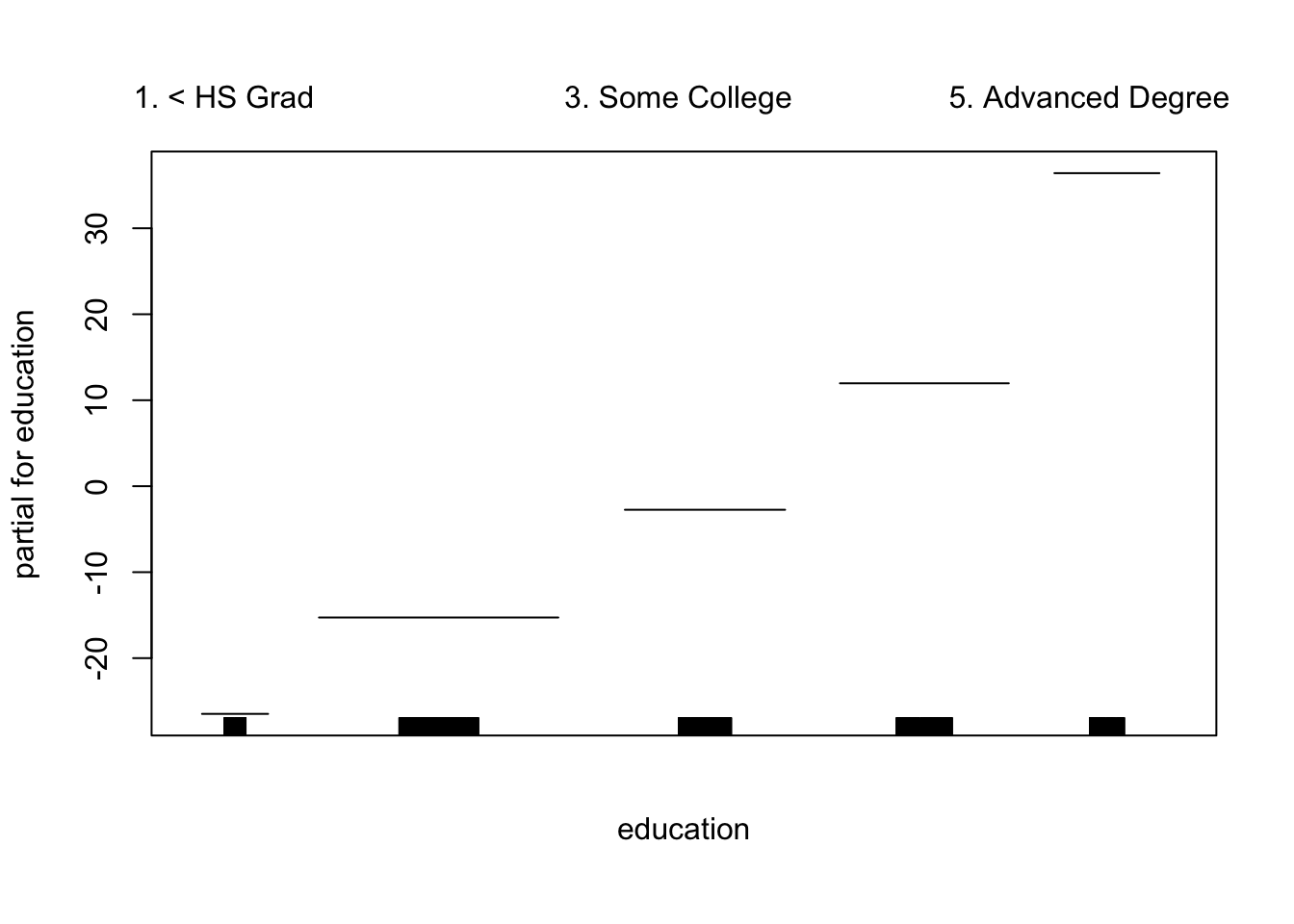
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言混合模型回归GBTM群组轨迹模型绘图可视化研究
R语言非参数回归预测摩托车事故、收入数据：局部回归、核回归、LOESS可视化
【视频讲解】非参数重采样bootstrap的逻辑回归Logistic应用及模型差异Python实现
Python个人收入影响因素模型构建：回归、决策树、梯度提升、岭回归
