
蒙特卡洛方法利用随机数从概率分布P(x)中生成样本,并从该分布中评估期望值,该期望值通常很复杂,不能用精确方法评估。
在贝叶斯推理中,P(x)通常是定义在一组随机变量上的联合后验分布。然而,从这个分布中获得独立样本并不容易,这取决于取样空间的维度。
因此,我们需要借助更复杂的蒙特卡洛方法来帮助简化这个问题;例如,重要性抽样、拒绝抽样、吉布斯抽样和Metropolis Hastings抽样。这些方法通常涉及从建议密度Q(x)中取样,以代替P(x)。
可下载资源
在重要性抽样中,我们从Q(x)中产生样本,并引入权重以考虑从不正确的分布中抽样。然后,我们对我们需要评估的估计器中的每个点的重要性进行调整。在拒绝抽样中,我们从提议分布Q(x)中抽取一个点,并计算出P(x)/Q(x)的比率。然后我们从U(0,1)分布中抽取一个随机数u;如果
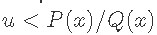
,我们就接受这个点x,否则就拒绝并回到Q(x)中抽取另一个点。吉布斯抽样是一种从至少两个维度的分布中抽样的方法。这里,提议分布Q(x)是以联合分布P(x)的条件分布来定义的。我们通过从后验条件中迭代抽样来模拟P(x)的后验样本,同时将其他变量设置在其当前值。
MCMC 的算法使用了一种接受、拒绝的条件判断结构,试想如果大部分采样值都被拒绝转移,就会导致采样了上百万次也没有使马尔可夫链收敛到平稳分布。这在实际中也是无法接受的。
Metropolis-Hastings (M-H) 采样
M-H 是两个算法创造者的名字!
M-H 采样用于解决MCMC接受率过低的问题。
我们从MCMC的细致平稳条件出发:
MCMC接受率过低主要原因是 过小的缘故,但是如果上式两端同时放大,细致平稳条件仍然可以满足:
Vanilla MCMC 对于这个值的计算方式是:
因此,一个直观且有效的改进方法就是:
即把等式两边的 中最大的一个扩大到 1,对应的也按相应比例放大。
Pseudocode
-
选定任意的马尔科夫链状态转移矩阵 Q,平稳分布
,设定状态转移次数阈值
,需要的样本个数
;
-
从任意简单概率分布开始,采样得到初始状态
;
-
for
to
:
-
从条件概率分布
中采样得到样本
-
从均匀分布采样u∼uniform[0,1]
-
如果
, 则接受转移
,即
-
否则不接受转移,即
样本集 即为我们需要的平稳分布对应的样本集。
很多时候,我们选择的马尔科夫链状态转移矩阵 Q 如果是对称矩阵,即满足 ,这时我们的接受率可以进一步简化为:
Gibbs 采样
M-H 在高维情况下有两个缺点:
-
计算 M-H 中的
是一笔很大的开销。
-
高维情况下需要以多元联合分布为采样目标,通常很难求出。
Gibbs采样思想
当联合分布未知或者难以取样,而每一个变量的条件分布则已知或者更易于取样的时候,我们就可以用Gibbs Sampling。Gibbs Sampling算法依次从每一个变量的分布中,以其他变量的当前值为条件,生成一个个体。易知,这个样本序列构成了一个Markov Chain,以及这个Markov Chain的平稳分布(stationary distribution)就是所需要的联合分布。
给定一个多元分布,相比对联合分布 积分然后求边缘分布
,从条件分布中直接取样的方法来的更加容易。
以二维数据为例, 假设 是一个二维联合数据分布,观察第一个特征维度相同的两个点
(上标为马尔可夫链的时间戳,下标为特征),容易发现下面两式成立:
由于两式的右边相等,因此我们有:
即
即在 这根一维线上,我们可以将条件概率分布
作为马尔科夫链的状态转移概率,则任意两个点之间的转移满足细致平稳条件!
同理,如果是前后两个采样点 ,此时是
不变,那么在这条一维的线上,条件概率分布
是其满足细致平稳条件的状态转移矩阵。
这也间接的导致了 MCMC 中的接受系数 恒等于1!即恒接受每一个采样点!
设 为新的采样点,k为唯一有变化的一维
二维Gibbs采样
-
平稳分布 $
,设定状态转移次数阈值
,需要的样本个数
;
-
从任意简单概率分布开始,采样得到初始状态
;
-
for
to
:
– 从条件概率分布中采样得到样本
– 从条件概率分布中采样得到样本
样本集 即为我们需要的平稳分布对应的样本集。
整个采样过程中,我们通过轮换坐标轴,采样的过程为:
虽然,重要性抽样和拒绝抽样需要Q(x)与P(x)相似(在高维问题中很难创建这样的密度),但当条件后验没有已知形式时,吉布斯抽样很难应用。
视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
视频
什么是Bootstrap自抽样及R语言Bootstrap线性回归预测置信区间
这一假设在更普遍的Metropolis-Hastings算法中可以放宽,在该算法中,候选样本被概率性地接受或拒绝。这种算法可以容纳对称和不对称的提议分布。该算法可以描述如下
初始化
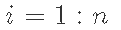
抽取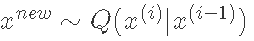
计算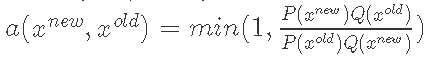
从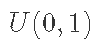 中抽取
中抽取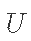
如果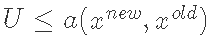 设
设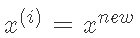
否则,设置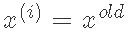
结束
吉布斯抽样是Metropolis Hastings的一个特例。它涉及一个总是被接受的提议(总是有一个Metropolis-Hastings比率为1)。
我们应用Metropolis Hastings算法来估计标准G-BLUP模型中回归系数的方差成分。
对于G-BLUP模型。
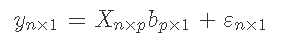
其中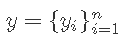 ,
,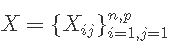 代表表型的向量和基因型的矩阵。
代表表型的向量和基因型的矩阵。 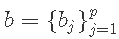 是标记效应的向量,
是标记效应的向量,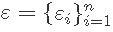 是模型残差的向量,残差为正态分布,均值为0,方差为
是模型残差的向量,残差为正态分布,均值为0,方差为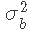 和
和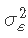 。
。
考虑到其余参数,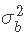 的条件后验密度为:
的条件后验密度为:
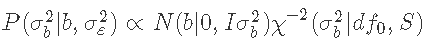
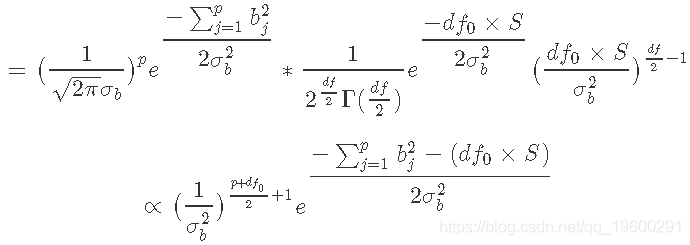
这是一个逆卡方分布。
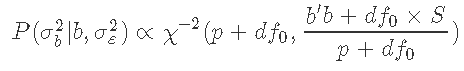
假设我们需要使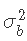 的先验尽可能地不具信息性。一种选择是设置
的先验尽可能地不具信息性。一种选择是设置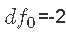 ,
,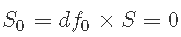 ,并使用拒绝抽样来估计
,并使用拒绝抽样来估计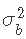 ;但是,设置S0=0可能会导致算法卡在0处。 因此,我们需要一个可以替代逆卡方分布的先验,并且可以非常灵活。为此,我们建议使用β分布。由于所得到的后验不是一个合适的分布,Metropolis Hastings算法将是获得
;但是,设置S0=0可能会导致算法卡在0处。 因此,我们需要一个可以替代逆卡方分布的先验,并且可以非常灵活。为此,我们建议使用β分布。由于所得到的后验不是一个合适的分布,Metropolis Hastings算法将是获得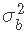 后验样本的一个好选择。
后验样本的一个好选择。
这里我们把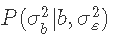 作为我们的提议分布Q。因此。
作为我们的提议分布Q。因此。
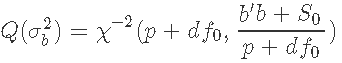
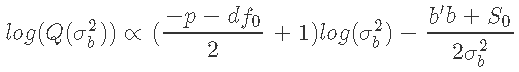
我们的目标分布是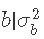 的正态似然与
的正态似然与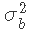 的β先验的乘积。由于β分布的域在0和1之间,我们用变量
的β先验的乘积。由于β分布的域在0和1之间,我们用变量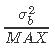 来代替β先验,其中MAX是一个确保大于
来代替β先验,其中MAX是一个确保大于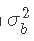 的数字,这样
的数字,这样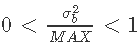 。
。
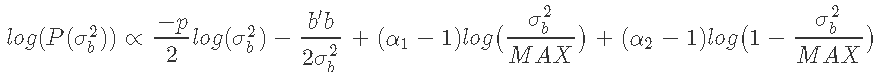
其中α1和α2是β分布的形状参数,其平均值由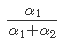 给出。
给出。
我们按照上面的算法步骤,计算出我们的接受率,如下所示。
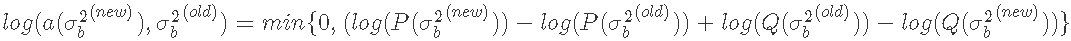
然后我们从均匀分布中抽取一个随机数u,如果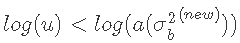 ,则接受样本点
,则接受样本点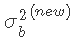 ,否则我们拒绝该点并保留当前值,再次迭代直至收敛。
,否则我们拒绝该点并保留当前值,再次迭代直至收敛。
Metropolis Hastings 算法
MetropolisHastings=function(p, ...)
chain\[1\]=x
for (i in 1:nIter) {
y\[i\] <-(SS+S0)/rchisq(df=DF,n=1,...)
logp.old\[i\]=-(p/2)\*log(chai) - (SS/(2\*chain) + (shape1-1)*(log(chain\[i\]/(MAX)))+(shape2-1)*(log(1-(chain\[i\]/(MAX))
logp.new\[i\]=-(p/2)\*log(y\[i\]) - (SS/(2\*y\[i\])) + (shape1-1)*(log(y\[i\]/(MAX)))+(shape2-1)*(log(1-(y\[i\]/(MAX))
chain\[i+1\] = ifelse (runif(1)<AP\[i\] , y\[i\], chain\[i\],...)吉布斯采样器
gibbs=function(p,...)
b = rnorm(p,0,sqrt(varb),...)
for (i in 1:Iter) {
chain\[i\] <-(S+S0)/rchisq(df=DF,n=1,...)随时关注您喜欢的主题
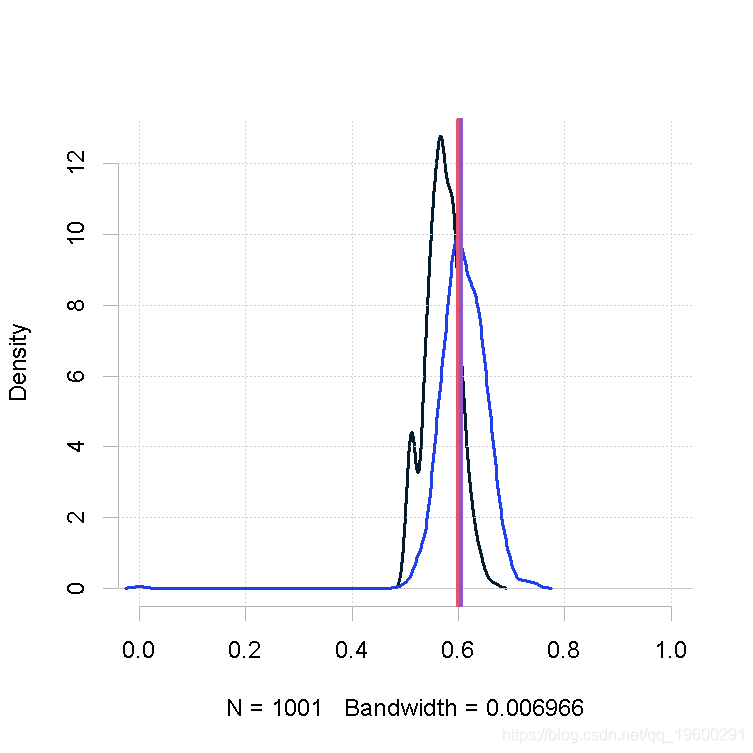
绘制图
plot = function(out1,out2)
plot(density(chain1),xlim=xlim)
lines(density(chain2),xlim=xlim)
abline(v=varb,col="red",lwd=3)设置参数

运行吉布斯采样器
##################
out1=gibbs(p=sample.small,...)
out2=gibbs(p=sample.large,...)在不同的情况下运行METROPOLIS HASTINGS
小样本量,先验
out.mh=mh(p=sample.small,nIter=nIter,varb=varb,shape1=shape.flat,shape2=shape.flat, MAX=MAX)

样本量小,β值的形状1参数大
p=sample.small
nIter
varb
shape.skew\[1\]
shape.skew\[2\]
MAX
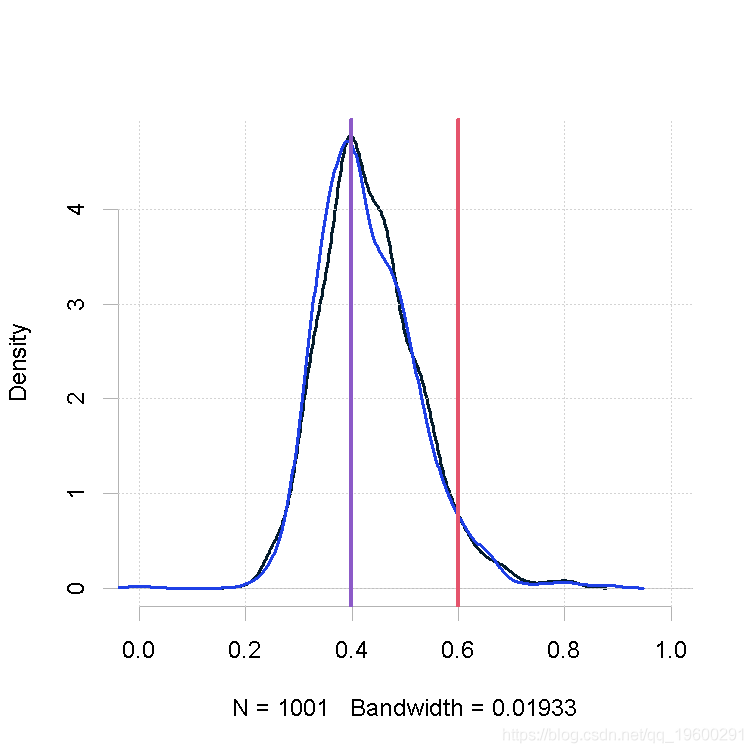
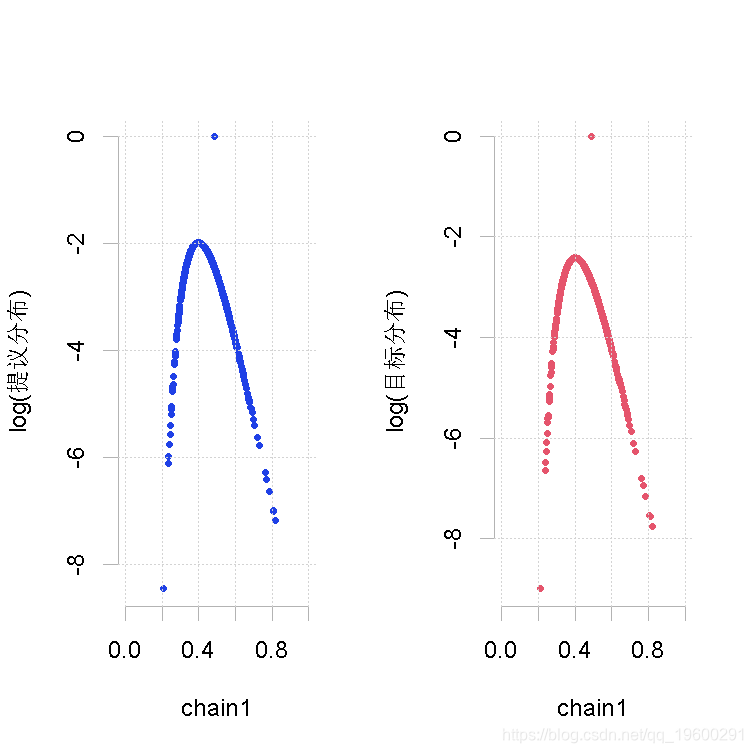
plot(out.mh, out.gs_1)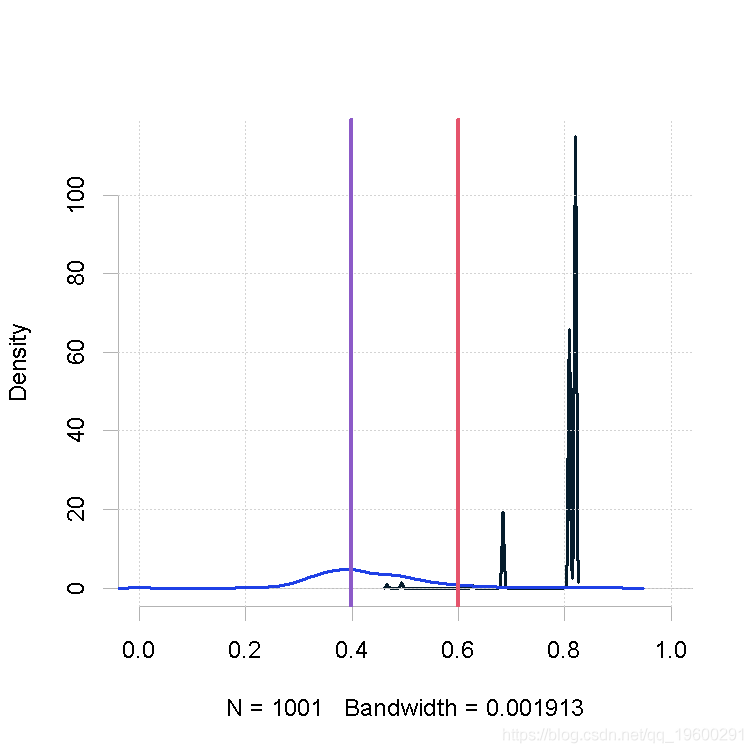

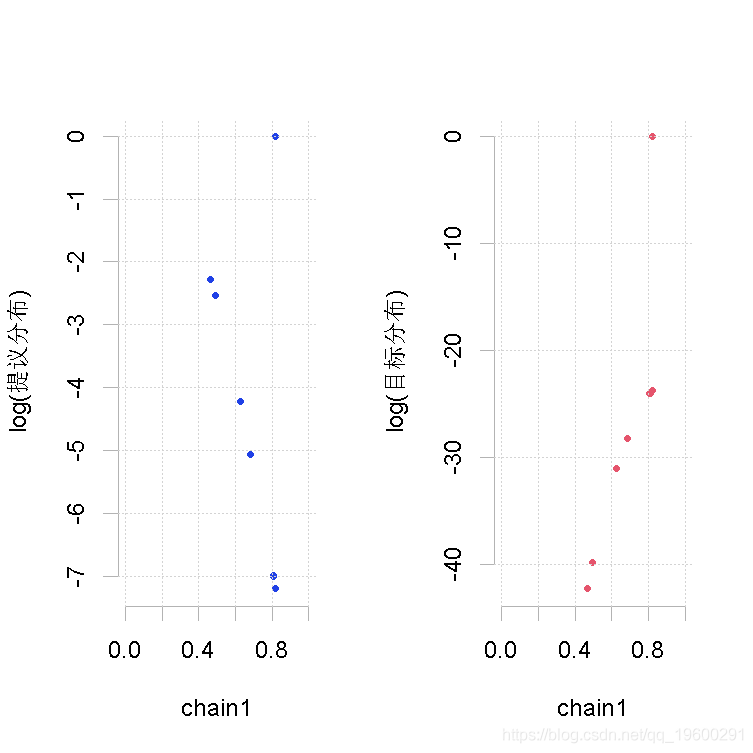
MetropolisHastings(p)
makeplot(out.mh, out.gs_1)样本量小,β值的形状1参数大
## Summary of chain for MH:
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.2097 0.2436 0.2524 0.2698 0.2978 0.4658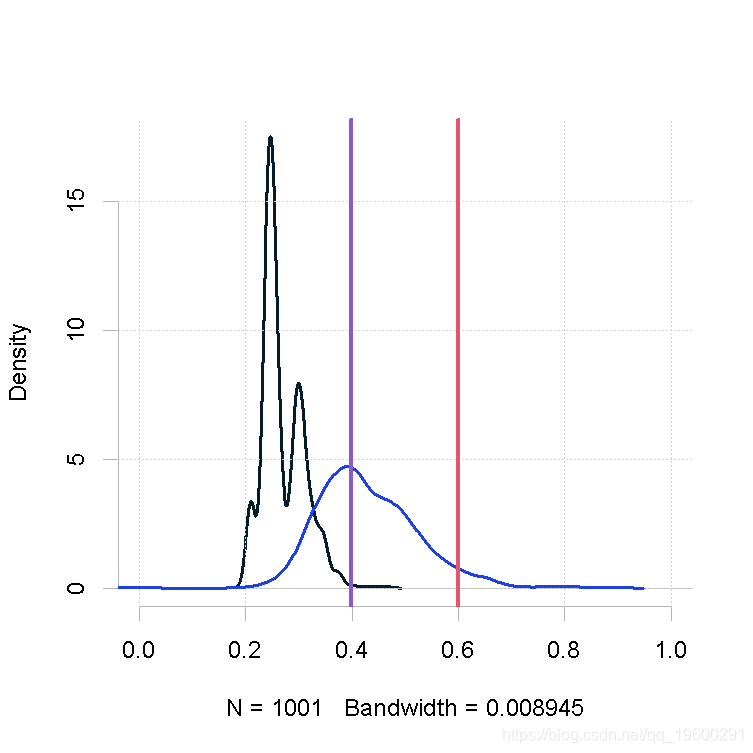

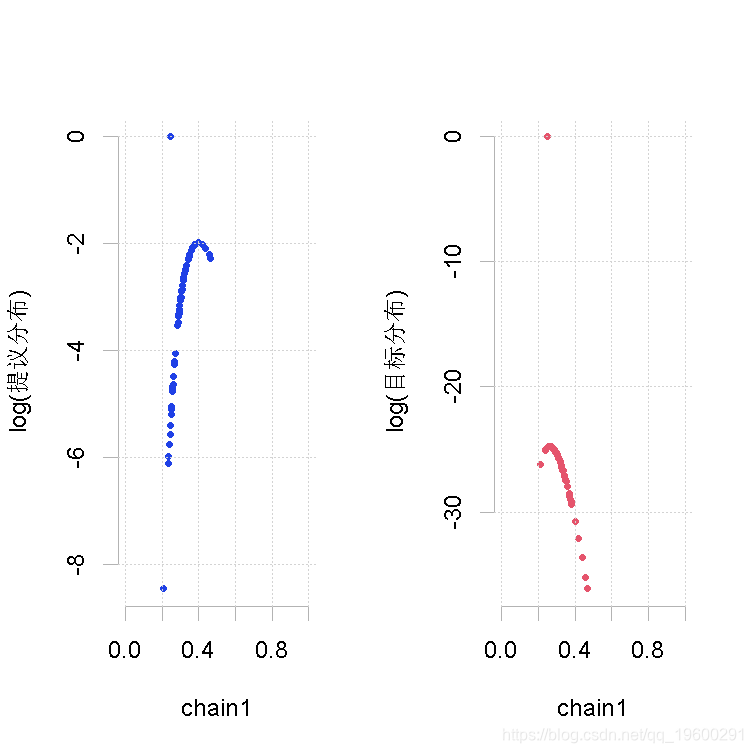
样本量小,β的形状参数相同(大)

plot(out.mh, out1)
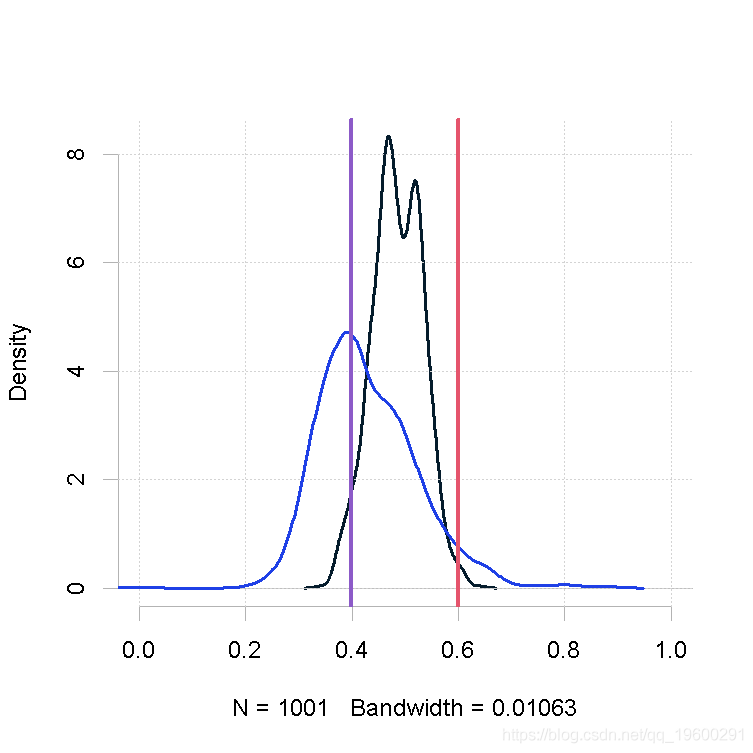
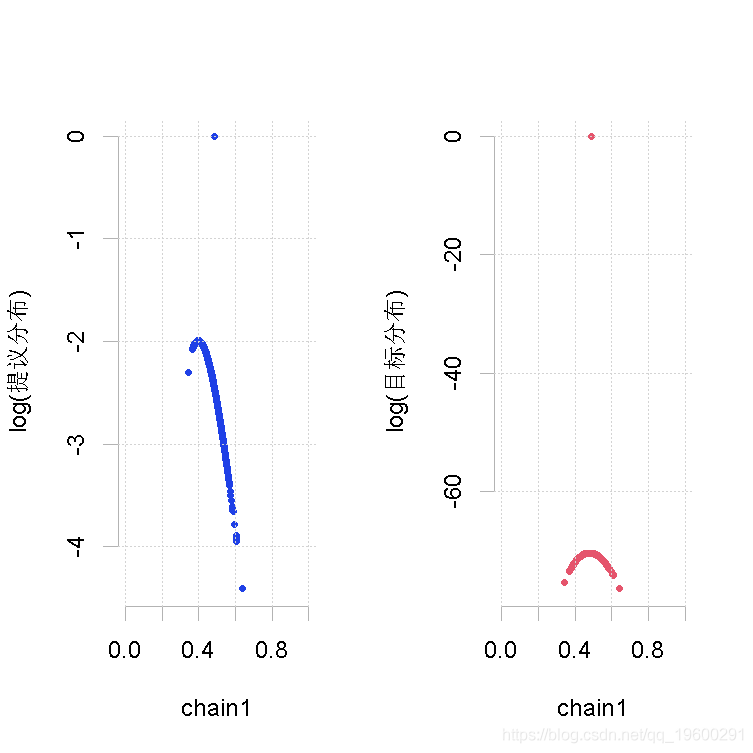
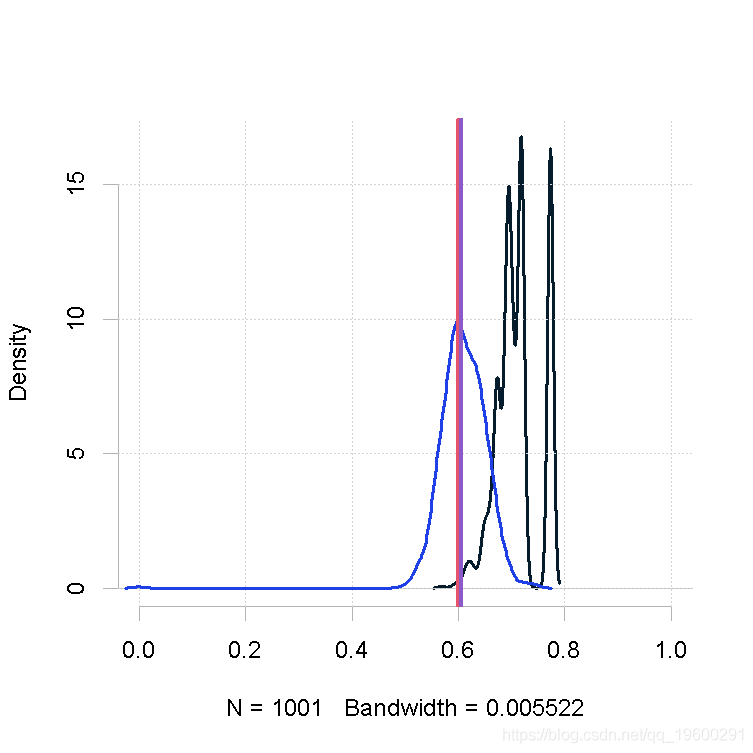
大的样本量,先验

plot(out.mh, out2)
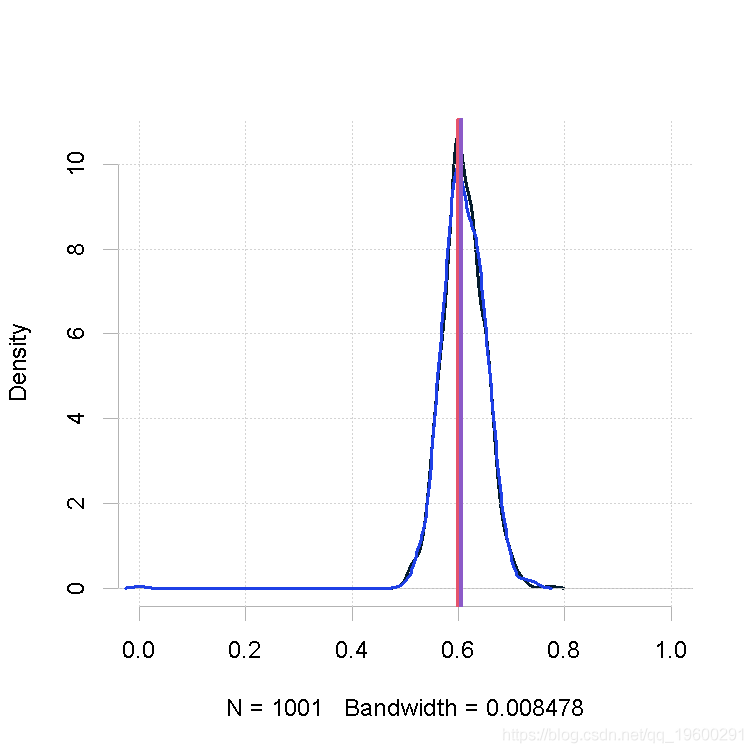
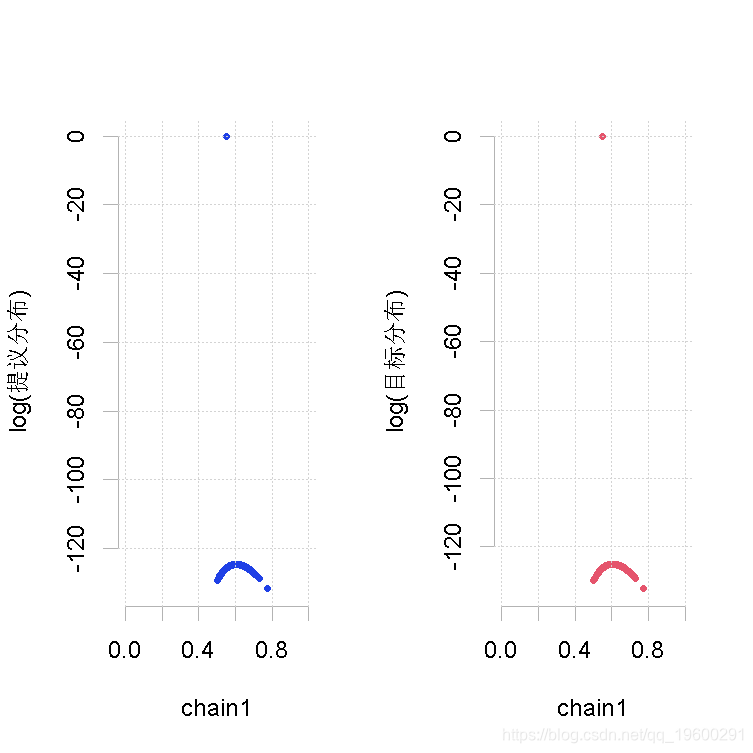
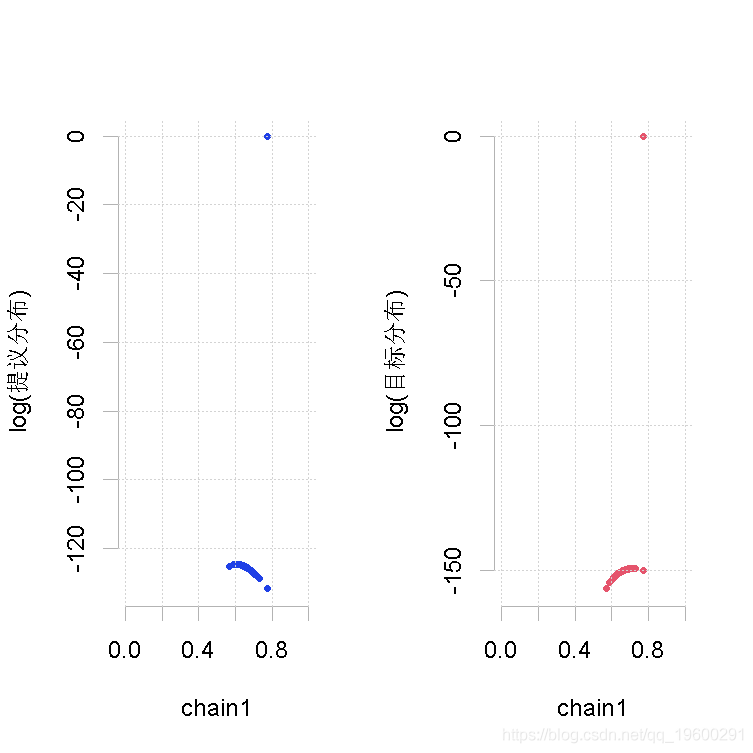
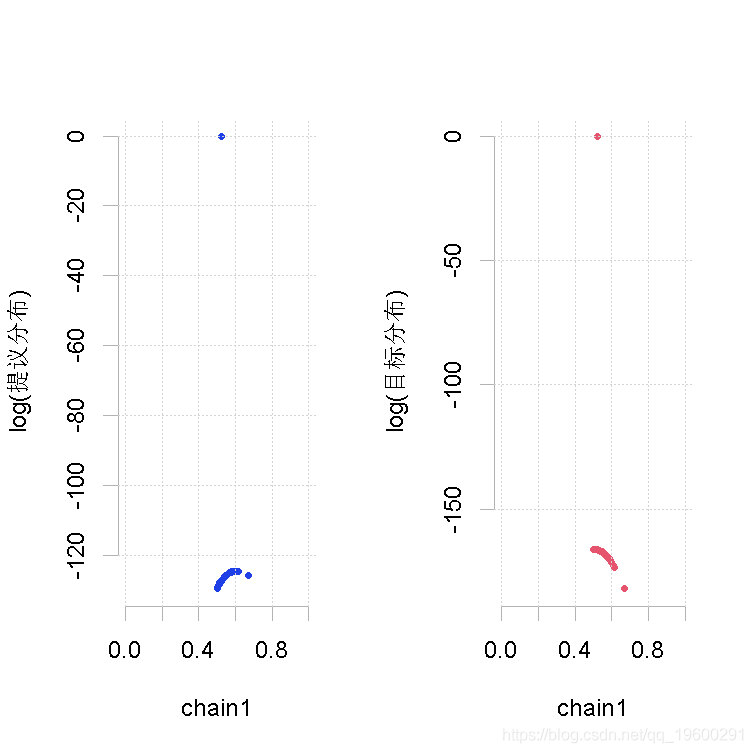
大样本量,形状1参数的β

plot(out.mh, out2)
大样本量,β值的大形状2参数

plot(out.mh, out_2)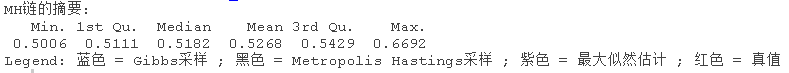
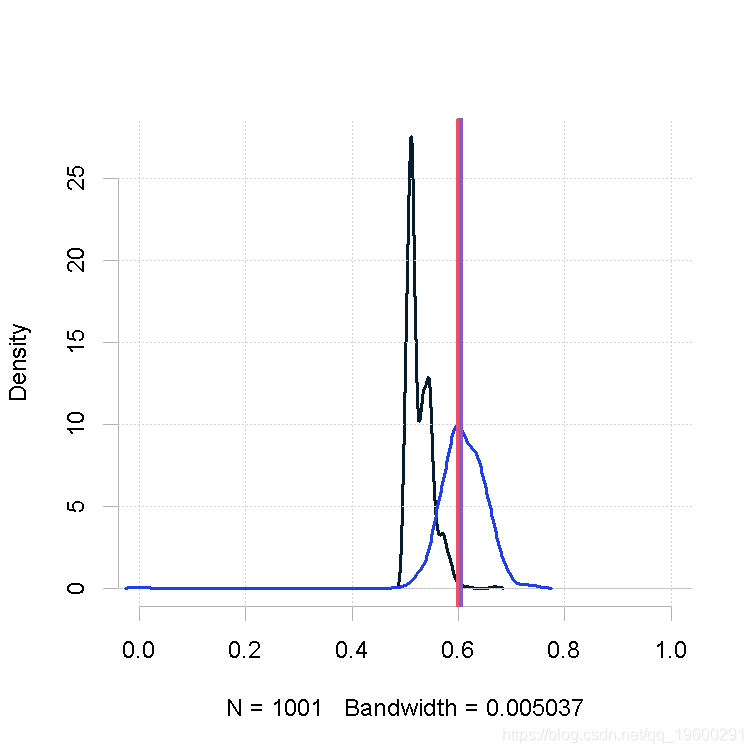
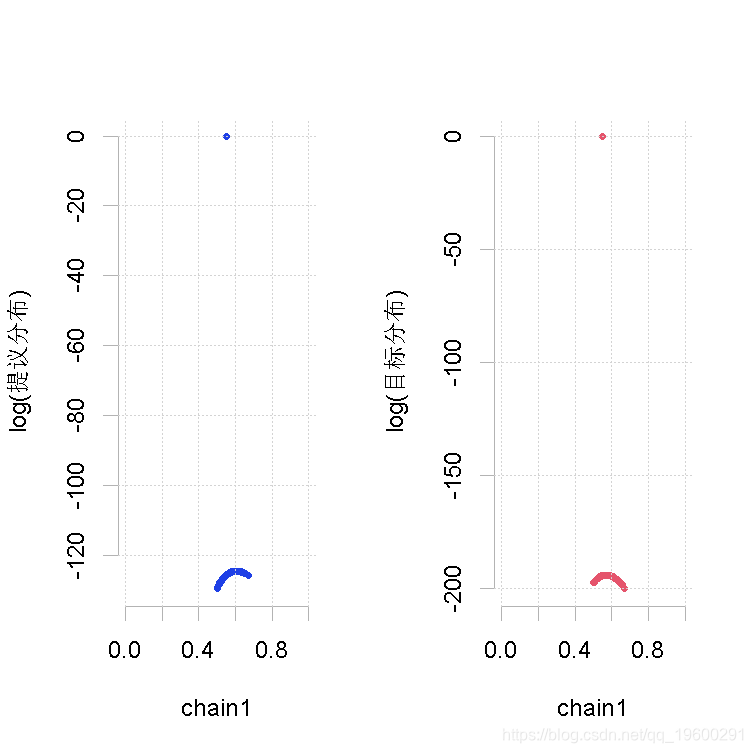
大样本量,β的形状参数相同(大)

plot(out.mh, out2)
参考文献
- Gelman, Andrew, et al. Bayesian data analysis. Vol. 2. London: Chapman & Hall/CRC, 2014.
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据
R语言优化沪深股票投资组合:粒子群优化算法PSO、重要性采样、均值-方差模型、梯度下降法|附代码数据 Python农作物种植策略研究GA-BP神经网络、蒙特卡洛算法、自注意力Stacking集成模型及粒子群算法PSO优化基于华北山区乡村农作物数据及地块数据
Python农作物种植策略研究GA-BP神经网络、蒙特卡洛算法、自注意力Stacking集成模型及粒子群算法PSO优化基于华北山区乡村农作物数据及地块数据 R语言贝叶斯Metropolis-Hastings采样 MCMC算法理解和应用可视化案例
R语言贝叶斯Metropolis-Hastings采样 MCMC算法理解和应用可视化案例 Python贝叶斯MCMC:Metropolis-Hastings、Gibbs抽样、分层模型、收敛性评估
Python贝叶斯MCMC:Metropolis-Hastings、Gibbs抽样、分层模型、收敛性评估



