本文首先展示了如何将数据导入 R。
然后，生成相关矩阵，然后进行两个预测变量回归分析。最后，展示了如何将矩阵输出为外部文件并将其用于回归。
数据输入和清理
可下载资源
首先，我们将加载所需的包。
library(dplyr) #用于清理数据 library(Hmisc) #相关系数的显着性
1.自变量选择偏差的权衡
（1）丢失重要变量
①剩余变量吸收了丢失的重要变量的信息，即用剩余变量进行了过度拟合；
②过于高估残差项（包含真实残差项的信息、忽略重要变量的信息）
（2）加入无关变量
①变量系数的估计偏差（大样本，无关变量会收敛于0）
②增加了模型参数估计的不确定性
③增加了R方的值，但是使得调整的R方减小
（3）两种合理估计线性回归系数 的方法
①一般情况模型变量的选择方法
a.将所有变量加入进行回归；
b.移除拟合效果最差的一个变量（尤其是不显著的变量）；
c.移除后继续采用线性回归模型进行拟合，再次移除不显著的变量；
d.重复以上步骤，直至所有变量的拟合结果都显著；
【注】通常选择显著性α在1%~0.1%（相应t值至少为2.57或3.29）。
②K折交叉检验
a.确定模型数量（有n个解释变量——每个变量选择有或无，通常有2^n个模型）
b.将数据分成相等数量的k个集合，其中k-1个集合作为训练集拟合回归方程，剩下的1个集合作为验证集；重复进行交叉拟合验证（总计有k次）。
c.每个模型都采用b的方式进行验证。
d.计算每个模型的总的残差项（验证k次）的和，选择残差项和或其均值最小的一组模型最为最优模型。
2.残差的异方差性
如果残差项的方差恒定不变（即为常数），则通常认定为同方差性，反之如果方差一直在变动并未恒定则认定为有异方差性。
【注】如果存在异方差性进行线性回归，则回归系数的假设检验以及置信区间的估计通常是有偏差的。
采用怀特检验法来验证异方差性：
例如检验有2个自变量的线性回归方程 ：
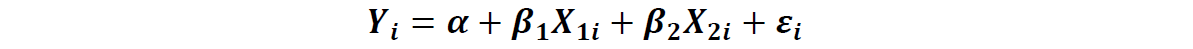
①采用OLS最小二乘法估计模型的残差
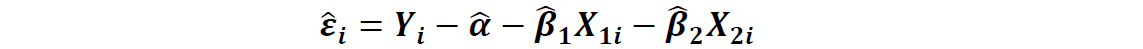
②将自变量和自变量之间的组合与残差的平方建立回归模型检验
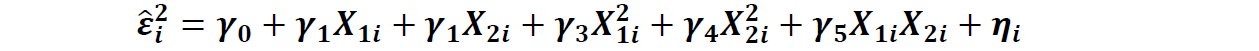
如果数据满足同方差性，则残差项的平方无法被任何自变量变量解释，即
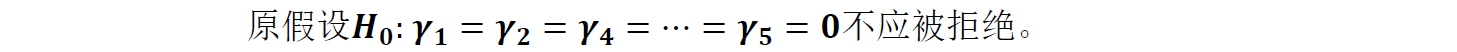
【注】残差项的方程的检验统计量的解释力度记为nR^2（即第②步中计算），其检验分布为卡方分布（自由度为——k(k+3)/2）
分析：
第一个为：LM统计量值;
第二个为：响应的p值，0.53远大于显著性水平0.05，因此接受原假设，即残差方差是一个常数;
第三个为：F统计量值，用来检验残差平方项与自变量之间是否独立，如果独立则表明残差方差齐性;
第四个为：F统计量对应的p值，也是远大于0.05的，因此进一步验证了残差方差的齐性。
3.多重共线性
(1)完美多重共线性
自变量之间存在相关系数=1的情况，即一个自变量可以被另一个自变量完全解释，完全替代。
(2)一般的多重共线性
①一个自变量或多个自变量之间可以大部分相互解释，存在较高的相关性
②当数据存在多重共线性时，通常发现系数之间有较强的显著关系，删除t统计量较小的(如t<1.96)
4.绘制残差图与异常值
（1）残差图即自变量与残差之间的散点图，异常值即偏离正常中心值较大的奇异点。
（2）异常值的判断：库克距离(Cook’s distance)
然后，我们将使用 Fortran 读入数据文件并稍微清理数据文件。
# 确保将您的工作目录设置为文件所在的位置
# 位于，例如setwd('D:/下载) 您可以在 R Studio 中通过转到
# 会话菜单 - '设置工作目录' - 到源文件
# 选择数据的一个子集进行分析，存储在新的
# 数据框
sub <- subset(des,case < 21 & case != 9)# != 表示不等于
#让我们看看数据文件
sub #注意 R 将原始数据中的空白单元格视为缺失，并将这些情况标记为 NA。 NA 是默认值
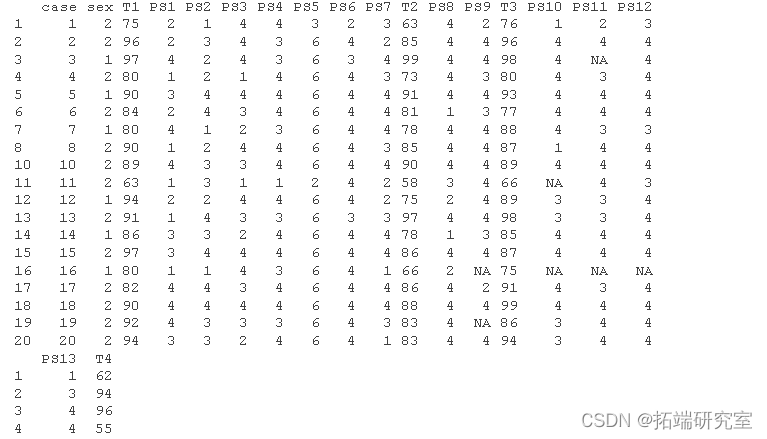
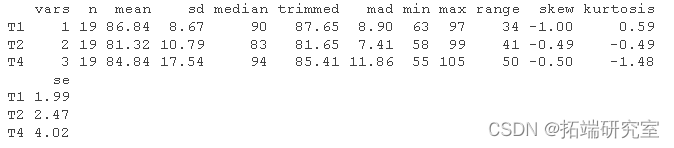
# 使用 dplyr 对特定测试进行子集化 select(sub, c(T1, T2, T4)) # 使用 psych 包获取描述
请注意，R 将原始数据中的空白单元格视为缺失，并将这些情况标记为 NA。NA 是 R 实现的默认缺失数据标签。
创建和导出相关矩阵
现在，我们将创建一个相关矩阵，并向您展示如何将相关矩阵导出到外部文件。请注意，创建的第一个相关矩阵使用选项“pairwise”，该选项对缺失数据执行成对删除。这通常是不可取的，因为它删除了变量，而不是整个案例，因此可能会使参数估计产生偏差。第二个选项，“complete”，对缺失数据实施列表删除，这比成对删除更可取，因为参数估计偏差较小（删除整个案例，而不仅仅是特定变量）。
# 在变量之间创建一个相关矩阵 cor <- cor( "pairwise.complete.obs", cor #相关矩阵
rcorr( test) # 相关性的显著性
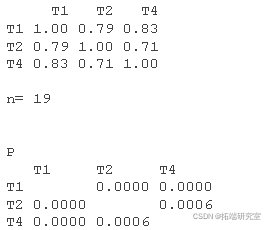
# 将相关矩阵保存到文件中 write.csv( cor, "PW.csv")
cor(test, method = "pear") cor #注意我们使用列表删除时的差异
# 将相关矩阵保存到硬盘上的文件中 write.csv(cor, "cor.csv")
多元回归
现在，我们将做一些多元回归。具体来说，我们将查看测试 1 和 2 是否预测测试4。我们还将检查一些模型假设，包括是否存在异常值以及检验之间是否存在多重共线性（方差膨胀因子或 VIF）。其中一些代码可帮助您将残差、预测值和其他案例诊断保存到数据帧中以供以后检查。请注意，lm 命令默认为按列表删除。
summary(model)
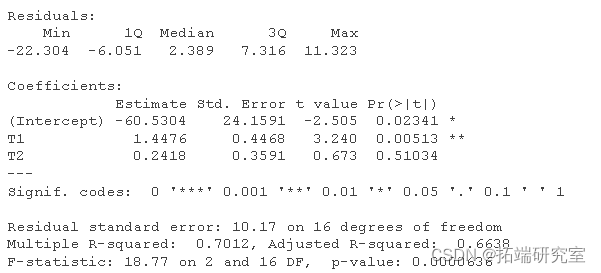
# 将拟合值和预测值保存到数据框 Predicted # 保存个案诊断（异常值） hatvalues(model) # 多重共线性检验 vif(model)
随时关注您喜欢的主题
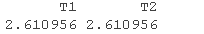
vcov(ol) #保存系数的方差协方差矩阵 cov(gdest) #保存原始数据的协方差矩阵
模型结果及其含义：
- 多重 R 平方 告诉您在给定模型中自变量的线性组合的情况下预测或解释的因变量的方差比例。
- 调整后的 R 平方 告诉您总体水平 R 平方值的估计值。
- 残差标准误差 告诉您残差的平均标准偏差（原始度量）。如果平方是均方误差 (MSE)，则包含在残差旁边的方差分析表中。
- F 统计量之后的显着性项 提供了针对没有预测变量的仅截距模型的综合检验（您的模型是否比仅平均值更好地预测您的结果？）
- 方差分析表 Mean Sq 残差的方差
- 方差膨胀因子 告诉您模型中的预测变量之间是否存在多重共线性。通常大于 10 的数字表示存在问题。越低越好。
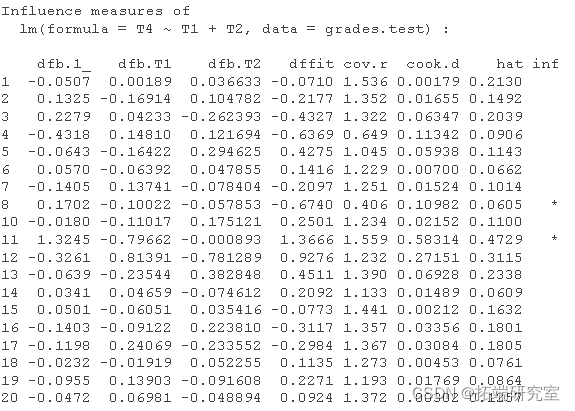
- 影响度量 提供了许多个案诊断。在此输出中，相应的列编号按各自的顺序表示：截距的 dfbeta、X1 的 dfbeta、x2 的 dfbeta、dffits（全局影响，或 Yhat（预测的 Y）基于案例的删除而改变了多少）、协方差比率（通过删除此观察值，估计的协方差矩阵的行列式的变化），库克的距离（影响），杠杆率（就独立预测变量的值而言，观察值有多不寻常？），显着性检验标志着案例作为潜在的异常值。请注意，发现异常值的一种方法是寻找超出均值 2 个标准差以上的残差（均值始终为 0）。
接下来，让我们绘制一些模型图。
# 制作模型的图表 plot(T4 ~ T1, data =test)
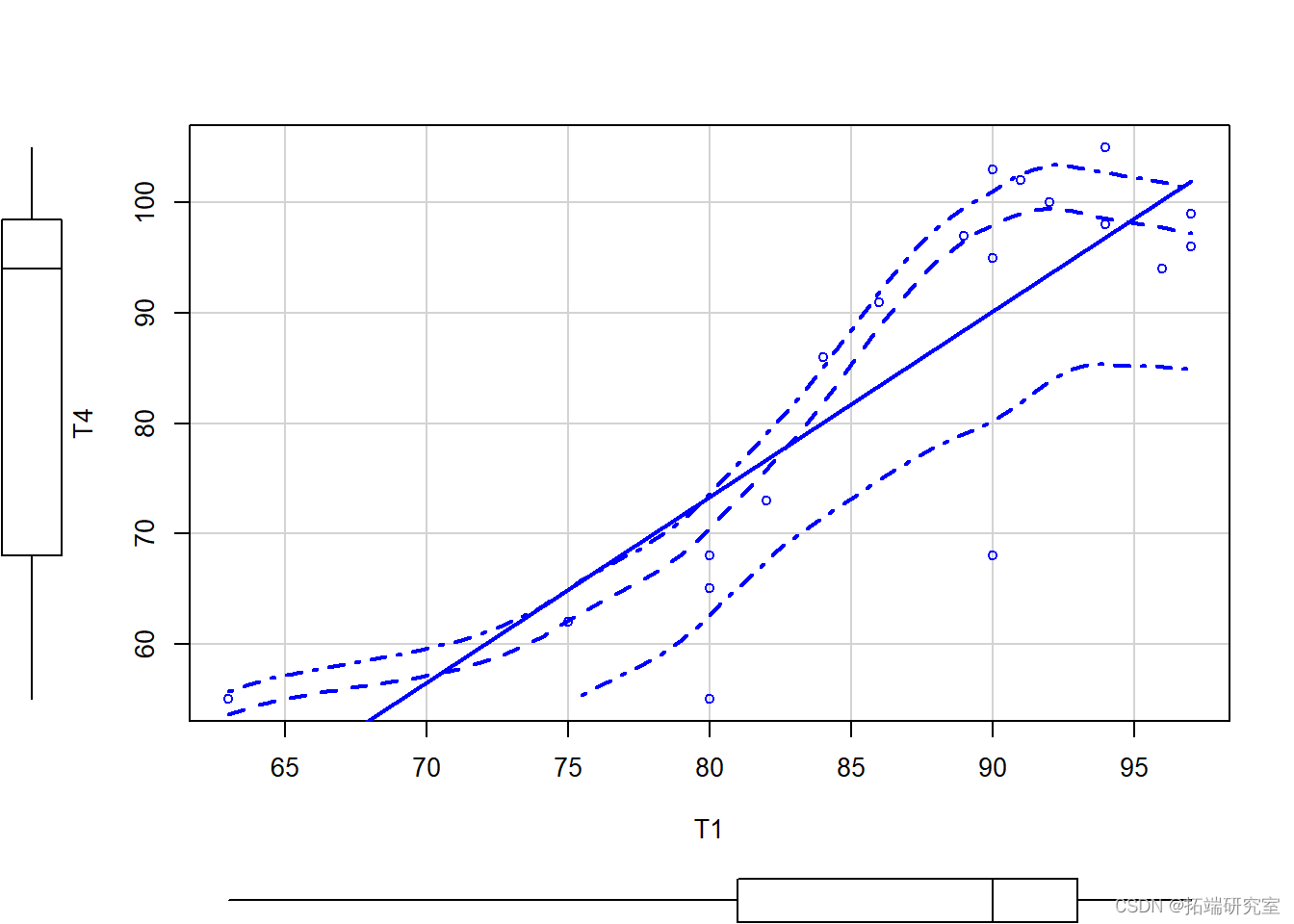
绿线表示线性最佳拟合，而红线表示LOESS(局部加权回归)_拟合。
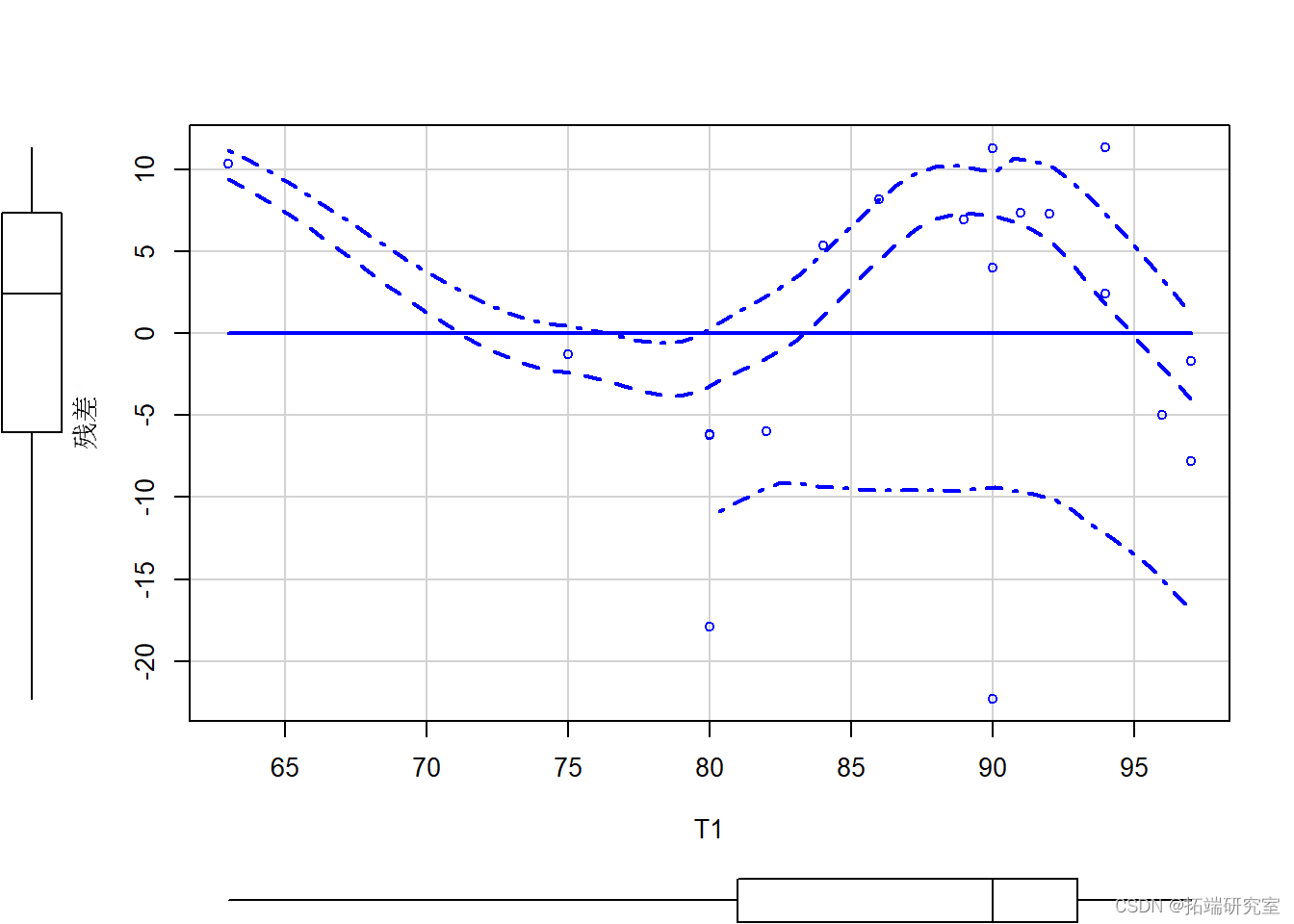
红色虚线表示LOESS(局部加权回归)_平滑拟合线的 +-1 标准误差。第一个散点图命令的额外参数标记每个数据点以帮助识别异常值。注意第二个图，如果残差是正态分布的，我们会有一条平坦的线而不是一条曲线。
使用多元回归来显示系数如何是残差的函数
现在，让我们看看系数是如何作为残差的函数的。我们将从之前的回归中构建 T1 的系数。首先，我们将创建 T4（标准）的残差，控制 T1 以外的预测变量。
residuals(mot4) #将残差保存在原始数据框中
接下来，我们为 T1（预测变量）创建残差，控制 T1 以外的预测变量。我们在 T2 上回归 T1，得到 Y=b0+b1T2，其中 Y 是 T1。残差是所有与 T2 无关的东西。
现在我们使用 T4 运行回归，将所有 T2 作为 DV 删除，T1 将所有 T2 作为自变量删除。
anova
summary(modf) #模型结果
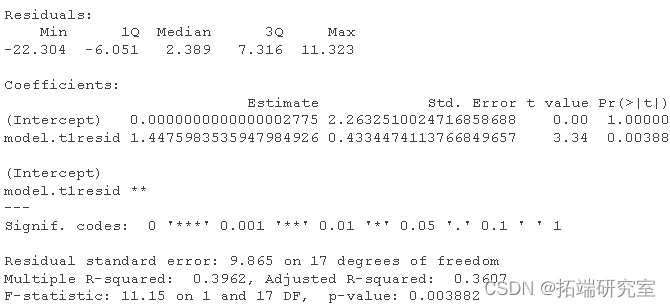
请注意，该回归系数与先前的两个预测器回归中的系数相同。接下来，我们将运行另一个以案例为DV的回归。我们将创建一个新的图表，以显示杠杆率只取决于预测因素而不是因变量。
anova(modeage)
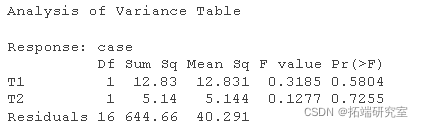
summary(modage)
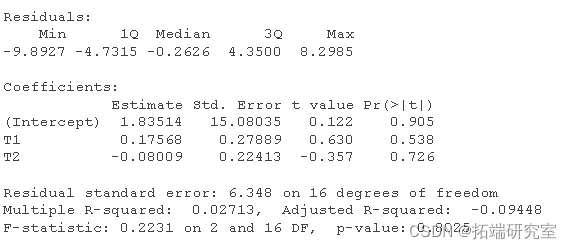
plot(lev ~ cae, data = grb)
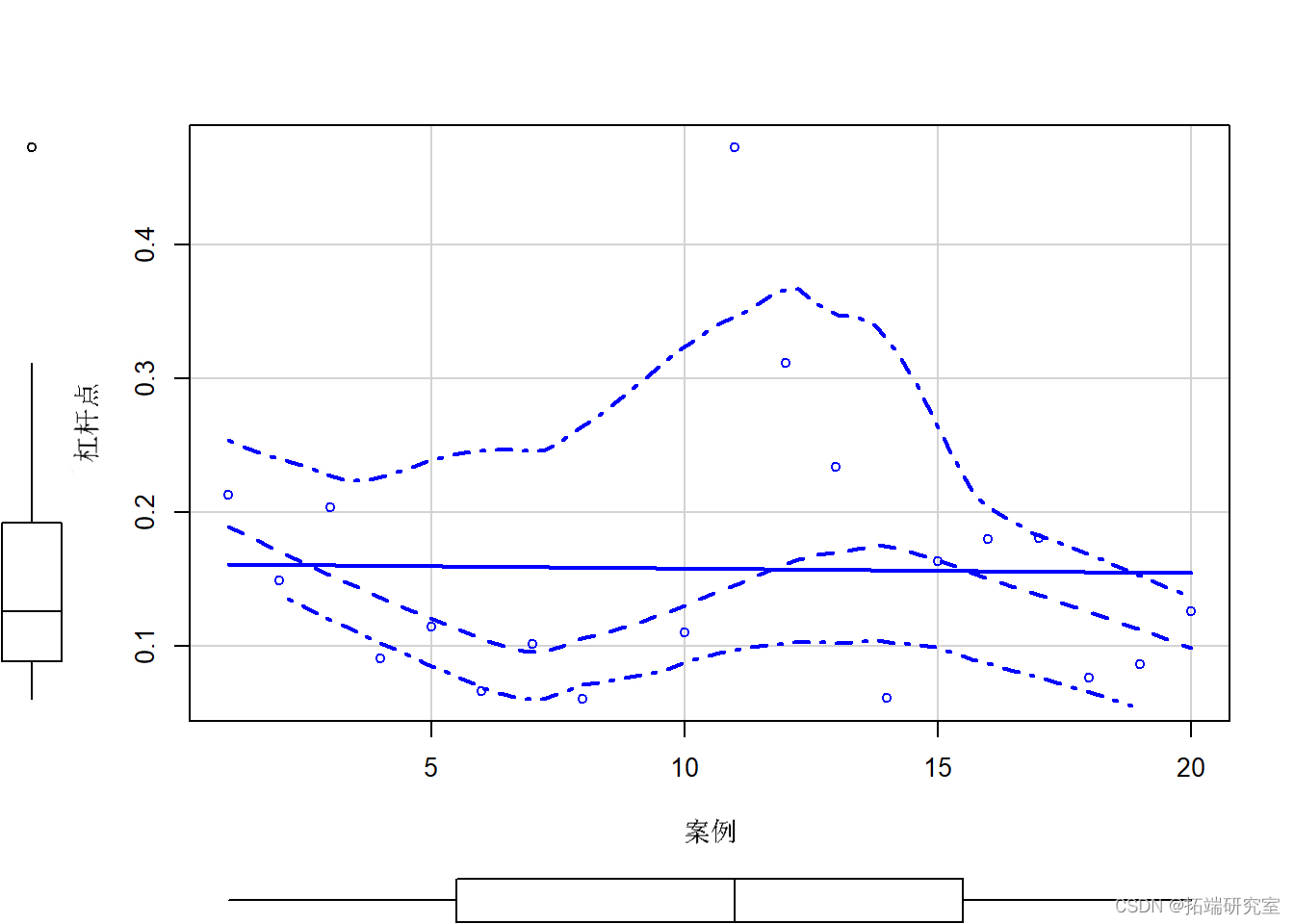
请注意，在SEM中，没有简单的距离或杠杆措施，但我们可以得到杠杆，因为它与DV是分开的。如果我们能找出一个极端的案例，我们在有和没有这个案例的情况下进行分析，以确定其影响。输出的变化将是对杠杆的测试。
现在我们制作测试之间关系的 3d 散点图。
plot(T1,T2, T4, 3d(model) #使用我们先前的模型来绘制一个回归平面
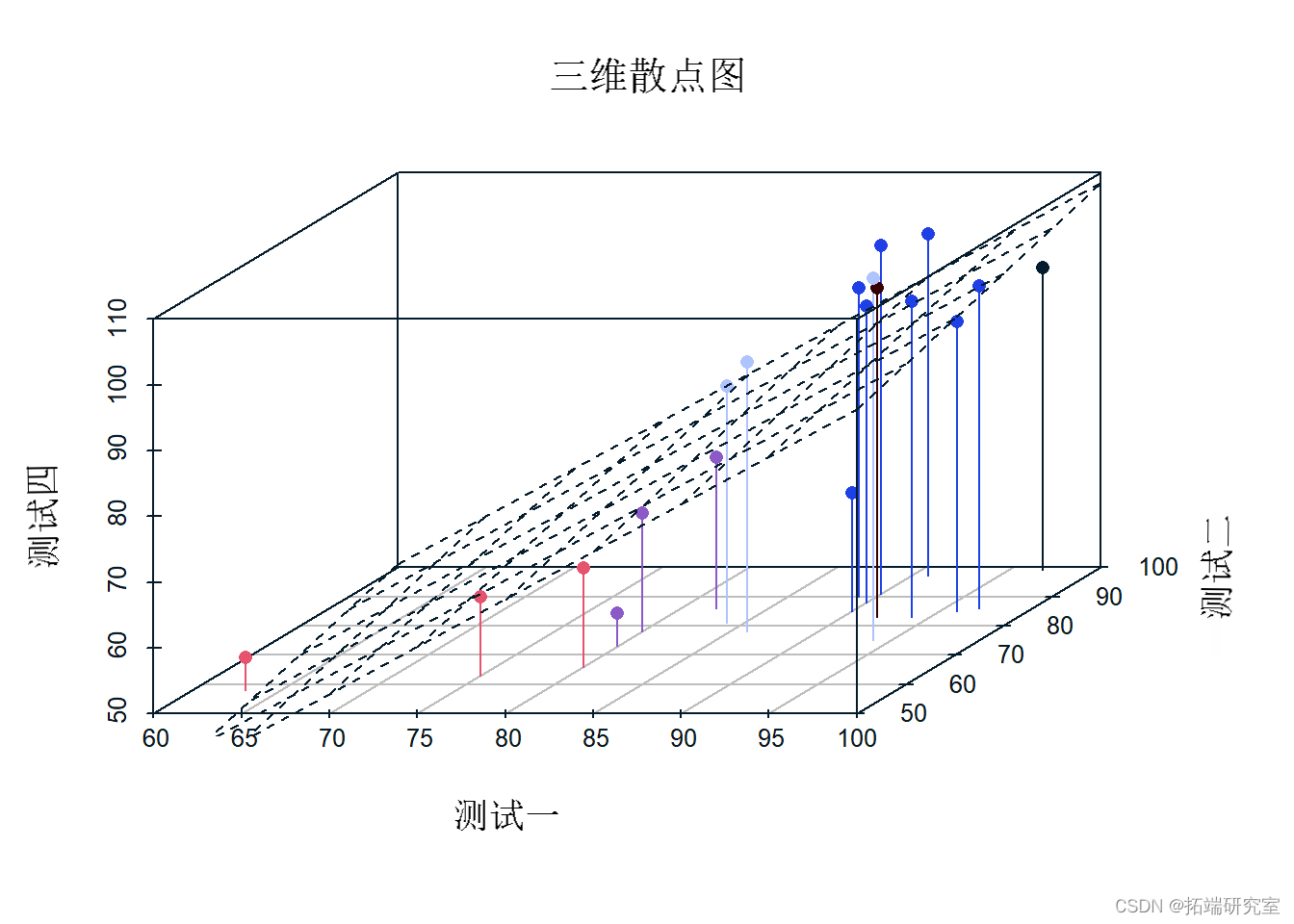
使用相关矩阵的多元回归
现在我们将展示如何仅使用相关矩阵进行回归。如果你想对提供相关和/或协方差矩阵的现有论文做额外的分析，但你无法获得这些论文的原始数据，那么这就非常有用。
#从你电脑上的文件中调入相关矩阵。
read.csv("cor.csv")
data.matrix(oaw) #从数据框架到矩阵的变化
#用相关矩阵做回归，没有原始数据
mdeor
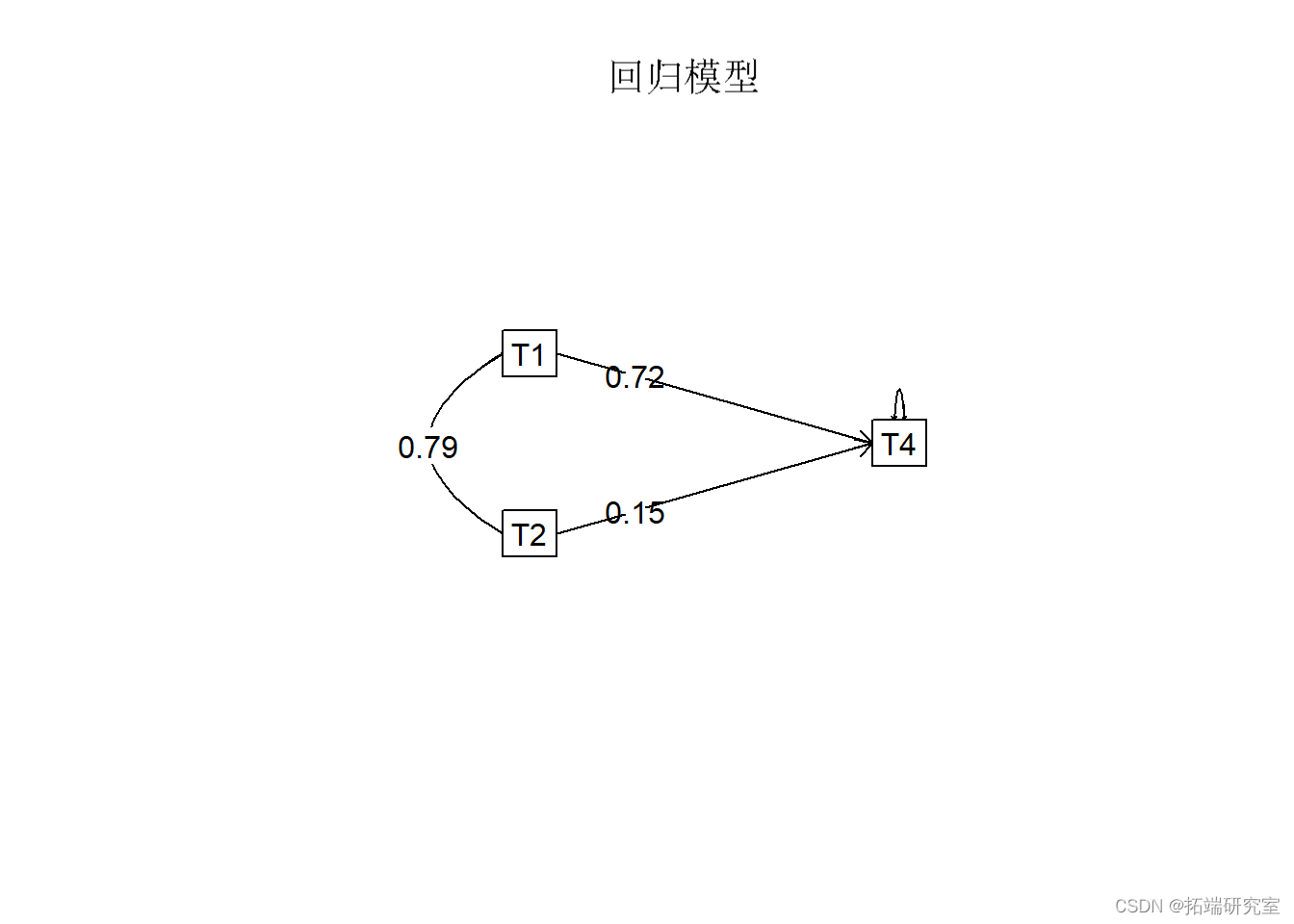
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频】N-Gram、逻辑回归反欺诈模型文本分析招聘网站欺诈可视化|附数据代码
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
R语言分类回归分析考研热现象分析与考研意愿价值变现
R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素
