R语言是一门非常方便的数据分析语言，它内置了许多处理矩阵的方法。

由Kaizong Ye，Liao Bao撰写

作为数据分析的一部分，我们要在有价证券矩阵的操作上做一些工作，只需几行代码。

有价证券数据矩阵在这里

要真正理解一般正规算子的谱分解是困难的，你几乎是绕不开“算子代数”的，我现在说一下思路：

1:有界的正规算子

设 $T$ 是希尔伯特空间上的有界线性算子，它可以生成一个交换的 $C^*$ 算子代数 $A_T$ ，而且它的极大理想可以和 $\sigma(T)$ 构成的对应，因此我们可以有一个从 $A_T$ 到 $C(\sigma(T))$ 的Gelfand map $\Gamma$ ，而且这个映射是 $*$ 代数同构的，也就是说，反过来，我们随便给一个连续函数 $u\in C(\sigma(T))$ ，那么 $\Gamma^{-1} (u)$ 是一个有界线性算子，特别的，我们可以有 $\Gamma^{-1}(1)=I$ , $\Gamma^{-1}(z)=T$ , 假设 $\sigma(T)=\{\lambda_1,\cdots,\lambda_n\}$ ，也就是说谱刚刚好是有限个点谱, 如果是一个矩阵，那么它的谱肯定是点谱。那么如果这个时候我们考虑函数 $\chi_{\lambda_i}$ ，也就是每一个点上的示性函数，在这个离散的情况下，这个函数是连续函数，所以我们可以构造 $E_i=\Gamma^{-1}(\chi_{\lambda_i})$ ,不难证明 $E_i$ 是正交投影算子，而且

$Tx:=\sum \lambda_i E_i x$ .

发现核心问题了吗？对于一般的 $\sigma(T)$ ,示性函数不是连续函数，也就是说Gelfand map没用了，可是投影算子是对应示性函数的，事实上设 $P$ 是投影算子，那么 $P^2=P$ ,如果它对应一个 $\sigma(T)$ 的函数 $u$ ，那么 $u^2(z)=u(z)$ ,所以在每个点这个函数只能是0或者1.

为了处理一般的算子，我们需要引入 $W^*$ -算子代数 $W_T$ ，本质上是 $A_T$ 在一个弱拓扑下的闭包，

最大的优点是可以让 $\Gamma$ 可以覆盖示性函数从而得到

$Tx:=\int \lambda d E_\lambda$ （这里也从离散和变为一般的积分）

“一般的对称算子“

首先根据上面的结论，对于任何unitary算子 $U$ ,因为它的谱肯定在一个圆环上，我们可以找到一个谱分解

$U=\int_0^{2\pi} e^{i\theta} d F_\theta$ ，

然后对于任何无界的对称算子 $A$ ，Cayley 变换 $B=\frac{A-i I}{A+iI}$ 是一个unitary算子，也就是说

$B=\int_0^{2\pi} e^{i\theta} d F_\theta$ ,如我们引入定义 $\lambda=-\cot(\theta/2), E(\lambda):=F(\theta)$ ，那么变换可以把一个圆环拉成实数轴，这个时候

$U=\int_{\mathbb{R}}\frac{\lambda -i}{\lambda+i} dE(\lambda)$ ,

如果我们定义算子

$C=\int_{\mathbb{R}} \lambda dE(\lambda)$ ，

可以证明 $C=A$ ，这里主要需要一些Cayley变换和对称算子的一些性质。

————————–

这种“通俗易通”地学习是容易的，但是却没啥价值，我这里引用一下某个数学家的话：一个东西如果你自己不能用，举不出例子，那么你就压根没学会。

 

D=read.table("secur.txt",header=TRUE)
M=marix(D\[,2:10\])
head(M\[,1:5\])

谱分解

对角线化和光谱分析之间的联系可以从以下文字中看出

 

> P=eigen(t(M)%*%M)$vectors
> P%*%diag(eigen(t(M)%*%M)$values)%*%t(P)

可下载资源

完整程序、数据和文档（word）

最受欢迎的见解

1.matlab偏最小二乘回归(PLSR)和主成分回归(PCR)

2.R语言高维数据的主成分pca、 t-SNE算法降维与可视化分析

3.主成分分析(PCA)基本原理及分析实例

4.基于R语言实现LASSO回归分析

5.使用LASSO回归预测股票收益数据分析

6.r语言中对lasso回归，ridge岭回归和elastic-net模型

7.r语言中的偏最小二乘回归pls-da数据分析

8.r语言中的偏最小二乘pls回归算法

9.R语言线性判别分析（LDA），二次判别分析（QDA）和正则判别分析（RDA）

首先是这个矩阵的谱分解与奇异值分解之间的联系

> sqrt(eigen(t(M)%*%M)$values)

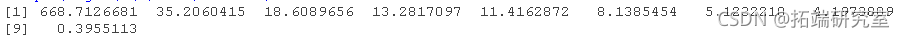
和其他矩阵乘积的谱分解

视频

主成分分析PCA降维方法和R语言分析葡萄酒可视化实例

探索见解 ➜

去bilibili观看 ➜

探索更多视频 ➜

> sqrt(eigen(M%*%t(M))$values)

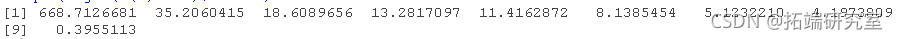
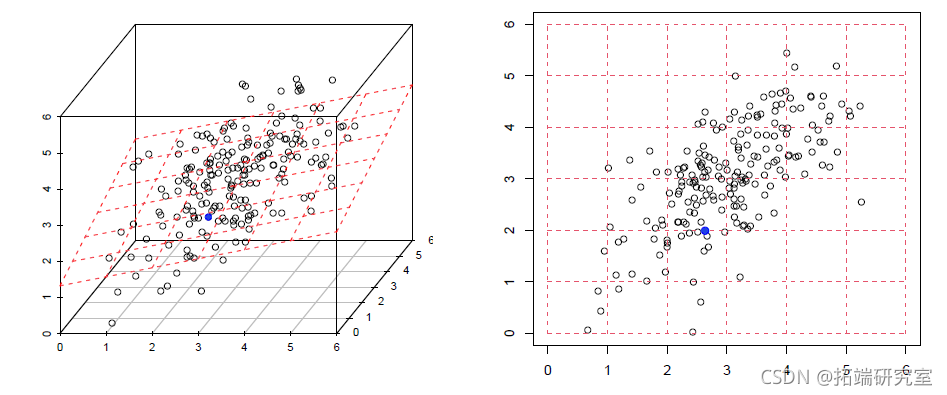
现在，为了更好地理解寻找有价证券的成分，让我们考虑两个变量

 

> sM=M\[,c(1,3)\]
> plot(sM)

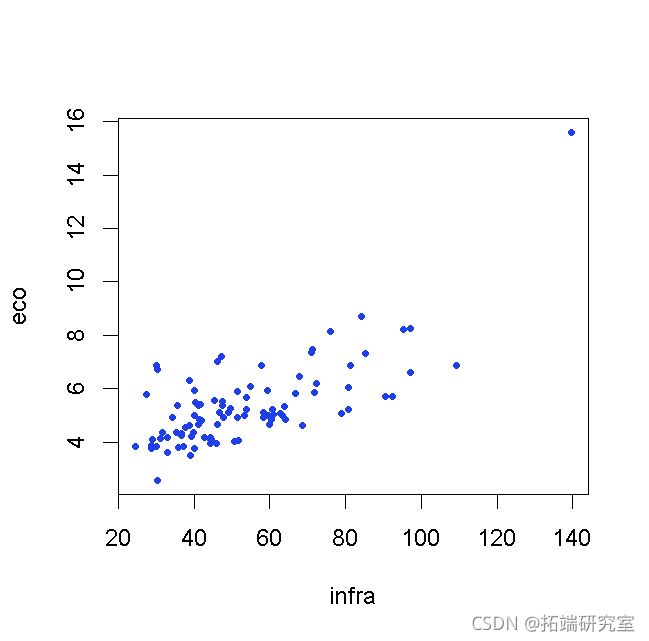
我们对变量标准化并减少变量（或改变度量）非常感兴趣

 

> sMcr=sM
> for(j in 1:2) sMcr\[,j\]=(sMcr\[,j\]-mean(sMcr\[,j\]))/sd(sMcr\[,j\])
> plot(sMcr)

python机器学习：推荐系统实现（以矩阵分解来协同过滤）

阅读文章 ➜

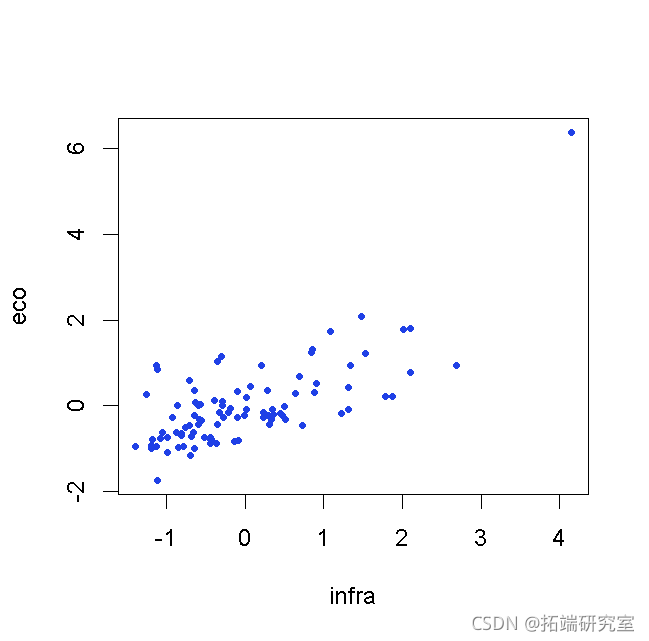
在对轴进行投影之前，先介绍两个函数

> pro_a=funcion(x,u
+   ps=ep(NA,nrow(x))
+   for(i i 1:nrow(x)) ps\[i=sm(x\[i*u)
+   return(ps)
+ }

> prj=function(x,u){
+   px=x
+   for(j in 1:lngh(u)){
+     px\[,j\]=pd_cal(xu)/srt(s(u^2))u\[j\]  
+   }
+   return(px)
+ }

随时关注您喜欢的主题

例如，如果我们在 x 轴上投影，

 

> point(poj(scr,c(1,0))

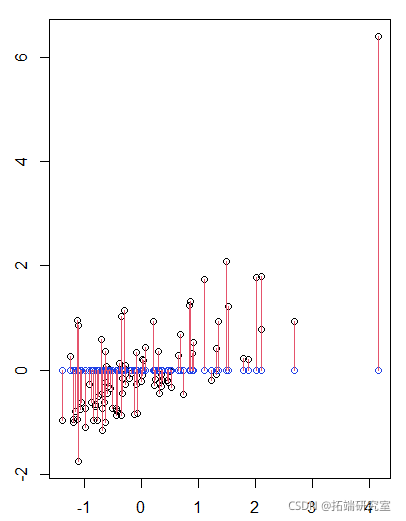
然后我们可以寻找轴的方向，这为我们提供具有最大惯性的点

> iner=function(x) sum(x^2)
> Thta=seq(0,3.492,length=01)
> V=unlslly(Theta,functinheta)ietie(roj(sMcrc(co(thet)sinheta)))
> plot(Theta,V,ype='l')

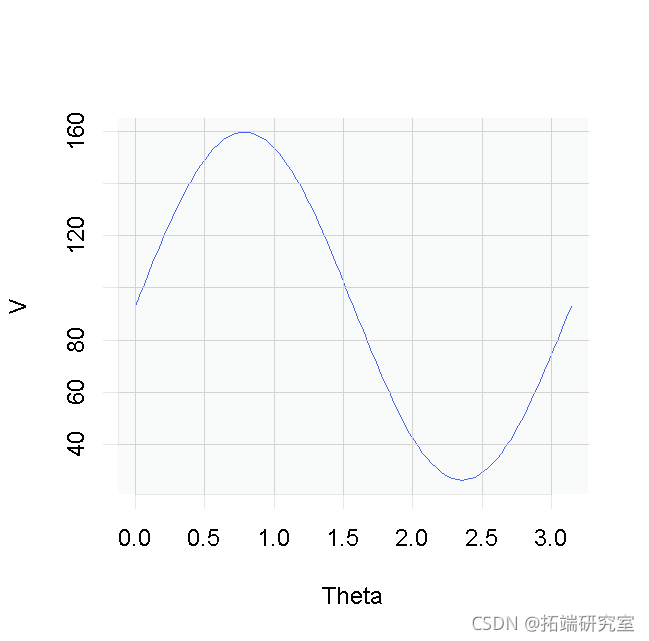
> (ange=optim(0,fun(iothet) -ertieprojsMcrc(s(teta),
si(ta)))$ar)

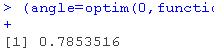
通过画图，我们得到

 

> plot(Mcr)

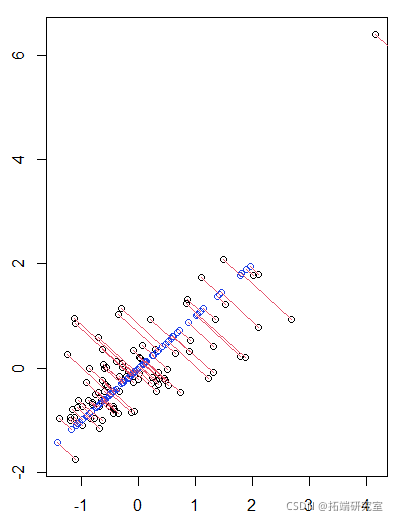
请注意，给出最大惯性的轴与谱分解的特征向量有关（与最大特征值相关的轴）。

>(cos(ngle),sin(ange))
\[1\] 0.7071 0.7070
> eigen(t(sMcr)%*%sMcr)

在开始主成分分析之前，我们需要操作数据矩阵，进行预测。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！