对于那些不熟悉“配对交易”概念的人来说几句话。
首先，您应该了解，每只股票的走势不是由公司业绩主导，而是由总体市场走势主导。
可下载资源
这就是许多“因子模型”的由来，驱动每只股票的因素是 _市场因素_，在大多数情况下，它与标准普尔指数近似。
因此，无论多么伟大的公司，它都经不起任何大规模的市场衰退。假设这样做，买入AMZN并卖出标准普尔指数（SPY），如果指数上涨，我就会亏损，因为我做空了它，但我希望AMZN会上涨，来补偿我在指数上的损失。
AMZN应该上涨，因为市场上涨了，而且它是一家好公司。反之，指数下跌，那么我就赢了，因为我做空了指数，我希望AMZN不会下跌那么多，吃掉我所有的利润。
AMZN没有因为市场而下降，但会上升，因为它是一家好公司。这样一来，我就表达了我对AMZN的看法，而没有承担因素/市场风险。所谓 “配对交易”，是因为我在做多和做空一对股票。这是对什么是配对交易的直白解释。
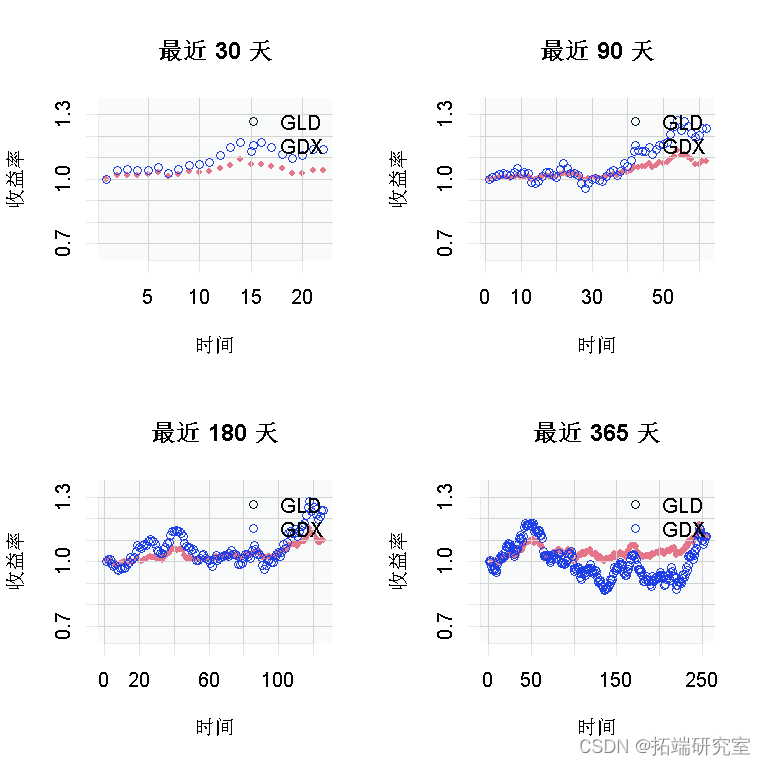
以下面这对黄金（GLD）和黄金矿工（GDX）为例，这是一个教科书式的例子，是一对 “一起走 “的组合。基本上，当黄金价格上涨时（GLD上涨），黄金矿工应该受益，所以GDX也应该上涨。请看一下。
for (i in 1:4){
plot(na.omit(Tiesy = 1)
points(na.omit(Tcke
legend('toprigh}
GLD 和 GDX 联动
该图显示相对于某个日期收益。现在，我们的计划是，当它们离得太远时，做多一个，做空另一个。那有什么问题呢？
右下方的图显示，在过去一年中，GLD的表现比GDX好得多。我想做空GLD，做多GDX，坐等收敛。我应该做多多少，做空多少？一比一？肯定是错的，因为GDX的价格是52.68，GLD的价格是155.23。也许把股票的数量相等，这样我在每个ETF中的多头和空头正好是10000元，所以做多188个GDX，做空64个GLD。然而，是不是其中一个增加1%，另一个就会增加1%？问题是，如果GLD上涨1%，GDX上涨1.5%，那么我需要持有1.5倍的GLD来保持我的价差不变，这很重要。举个例子，假设我持有相同的价值，做空GLD 10000，做多GDX 10000，但是这两者之间的关系是，当GDX上涨1%，GLD上涨1.5%。当它们共同上涨时，我的损益会发生什么？我的损失是0.5%，因为我做空GLD，而GLD的涨幅比GDX大…
为了解决这个问题，正在做的是估计这两个组成部分之间的关系。用回归法来做：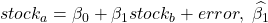
是我需要从 
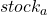补偿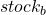 
移动的资金。我们运行。
尽管这种方法很有吸引力，但它远非“久经考验”。首先，我们应该使用收益还是实际价格？学院喜欢前者，实践者喜欢后者。如果您想知道，情况就不一样了：
plot(Tc[,i,2]) ~ na.omit(Tkr[,i,1]lm )
abline(lm)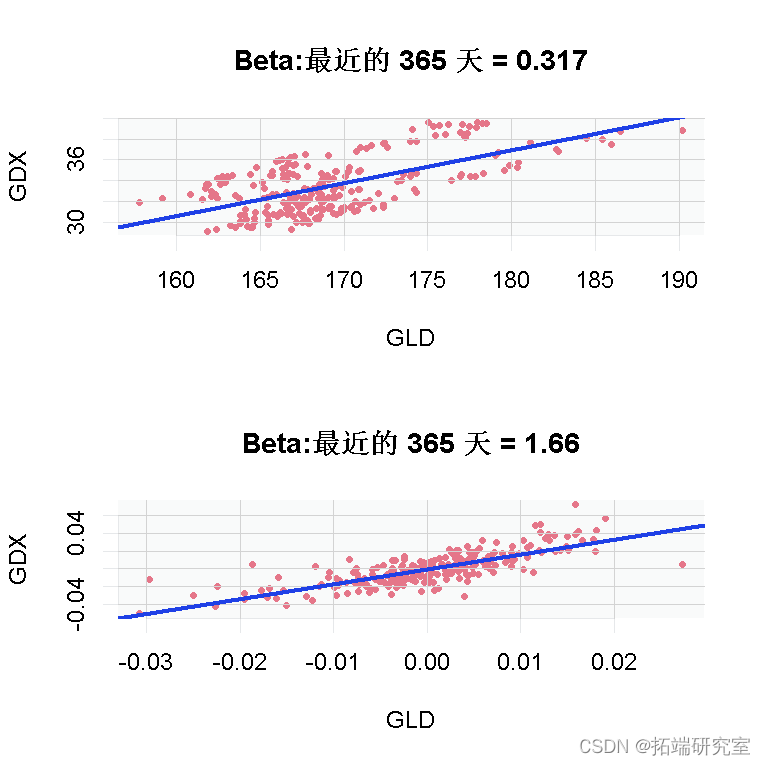
上图是基于价格的估计，它表明我应该为每 1 个GLD 做多 0.317个 GDX 。
下图显示了基于收益的相同估计，GDX 的每个百分比平均有 1.66 个GLD 中的百分比。
更重要的是，上述的回归受到了基本假设的影响，即右边的变量是常数，而左边的变量是随机的，它有一个误差项。事实上，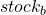
也是随机的，所以当我们切换回归中的变量时，在 “Y “插入GDX，我们得到不同的结果。
随时关注您喜欢的主题
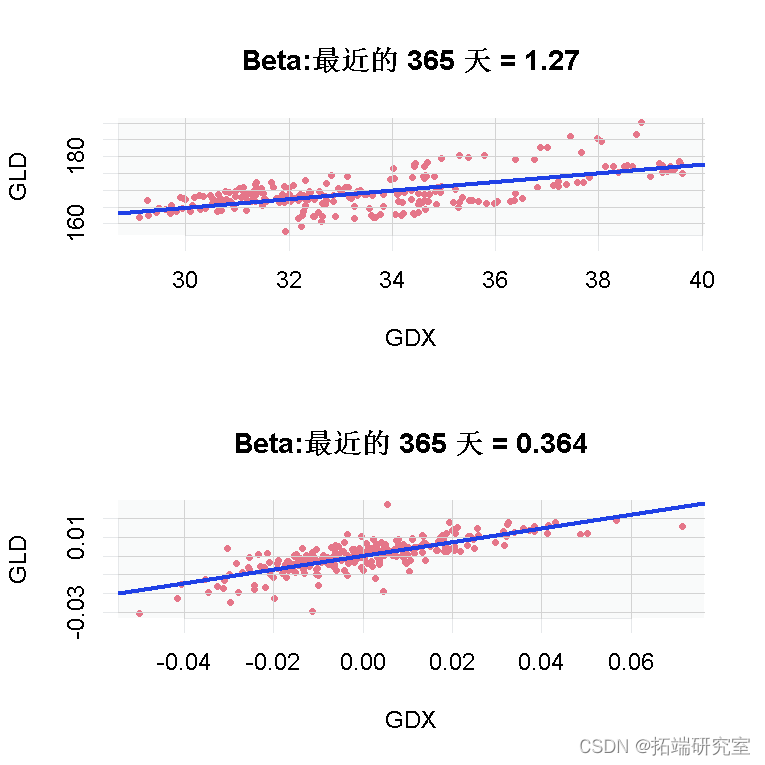
可以看到结果有所变化，GLD不是一个给定的常数，而是它本身就是一个随机变量。
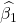随着时间的推移不是恒定的，所以我不知道要使用多少观察。看看：
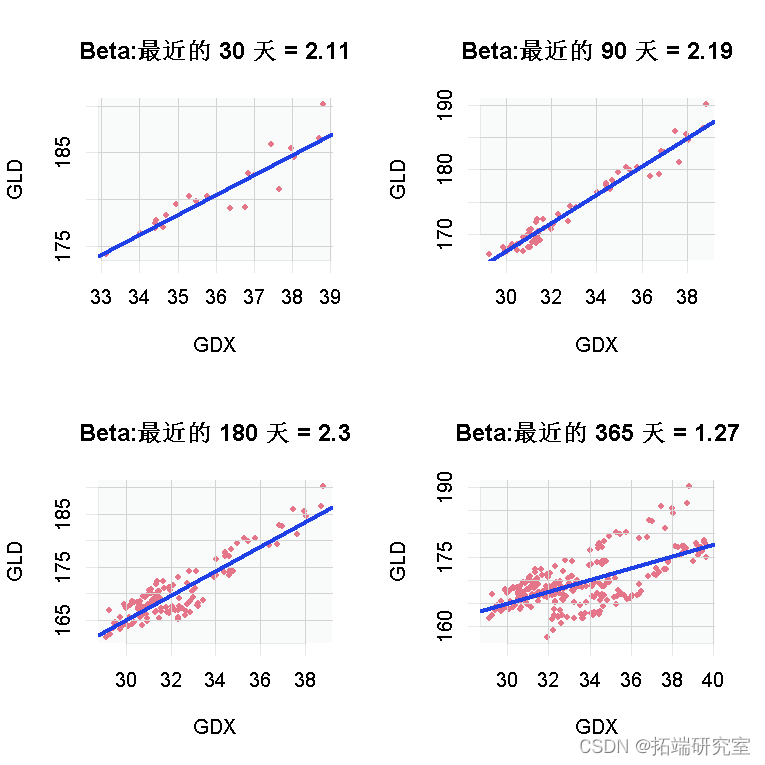
如果您颠倒 LHS 和 RHS 变量的顺序，收益当然也是如此。
可能的解决方案是考虑您的投资时间范围，例如，如果您计划持有几个月，您可以使用 365 天测试。我还尝试对观察结果进行加权，来确定我应该从每个观察中保留多少。
在理论上，理论和实践之间有很强的联系，但在实践中却没有。我在这里展示了配对交易中的一些问题。首先，我们不知道应该用哪种方法来估计关系，是价格还是收益。其次，我们不知道使用哪个时间段，由于关系不是恒定的，所以这很重要。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
R语言分类回归分析考研热现象分析与考研意愿价值变现
R语言神经网络模型金融应用预测上证指数时间序列可视化
SPSS用多元逐步回归模型对上证指数预测、描述统计和相关分析可视化研究
