极值理论对样本尾部分布的极值指数的估计方法主要有两类：半参数方法和全 参数方法，前者主要是基于分布尾部的 Hill 估计量，后者则主要基于广义帕累托分布。
尾部指数的希尔HILL统计量估计。
更具体地说，我们看到如果
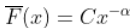
， 和
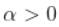
，然后希尔HILL估计为
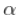
极值理论是概率论与数理统计方向的一个重要分支，极大值和极小值统称为极 值，其极限分布问题即为极值理论，极值理论建立的极值分布模型只以分布的尾部 数据为样本，它能够非常精准的描绘分布尾部的分位数，是一门用来预测异常现象 或者小概率事件风险的模型技术，如今在气象、金融、保险、材料强度、洪水、地 震等许多领域有广泛的应用。
近几年来，极值理论的研究取得了很大进展，对机制 理论感兴趣的，已由最初的概率论的研究人员及实际应用部门，发展到现在的主流 统计学家，在各个领域都在不断地进行理论与应用的创新。 在极值估计中，对极值指数(Extreme Value Index)的估计构成了极值估计的主要 内容，极值指数反映了尾部数据分布的变化速率，目前来说，极值理论对数据分布 尾部指数的估计方法主要有两类：半参数方法和参数方法，前者主要是基于分布尾 部的Hill估计量，后者则是基于广义Pareto分布。此外，许多学者对的估计提出了多 种估计量，如Pickands估计、Moment估计、Hill估计、指数回归模型估计、基于GPD 分布的POT估计法等。
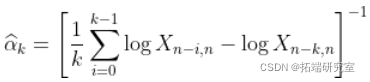
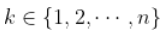。 然后 
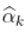在某种意义上满足某种一致性 
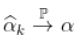,如果 
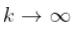，即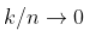 
（在收敛速度的附加假设下， 
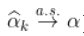）。此外，在附加的技术条件下
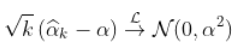
为了说明这一点，请考虑以下代码。首先，让我们考虑一个帕累托生存函数，以及相关的分位数函数
> Q=fuction(p){unro(funion(x) S(x)-(1-p),loer=1,per=1e+9)$root}
我们将考虑更复杂的生存函数。这是生存函数和分位数函数，
> plot(u,Veie(Q)(u),type="l")
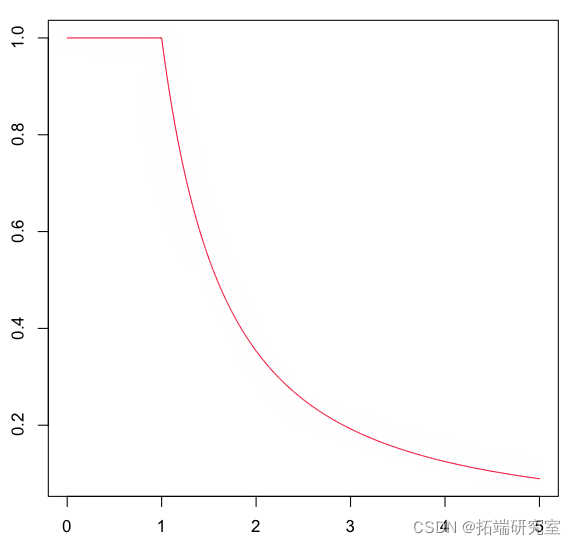
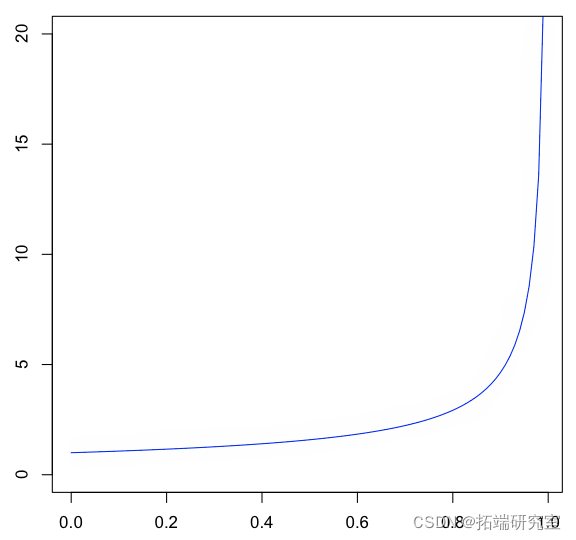
在这里，我们需要 分位数函数从这个分布中生成一个随机样本，
> X=Vectorize(Q)(runif(n))
hill统计量在这里
> abline(h=alpha)
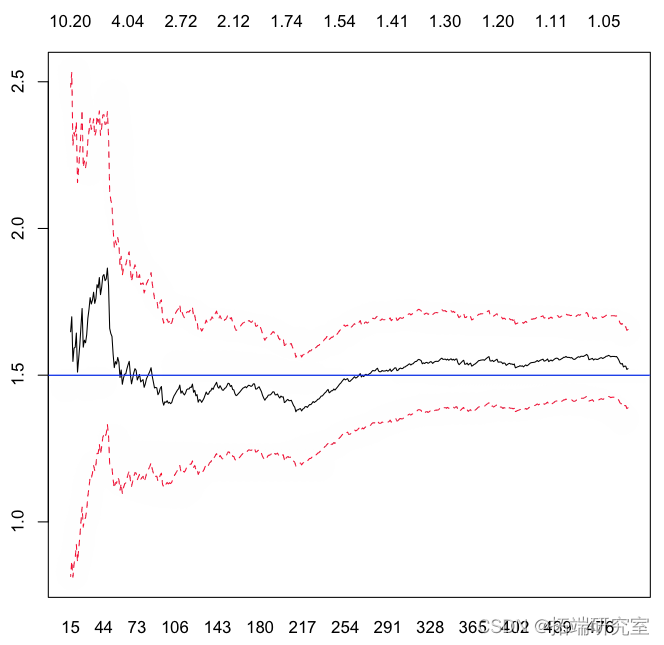
我们现在可以生成数千个随机样本，并查看这些估计器（对于某些特定的 的）。
> for(s in 1:ns){
+ X=Vectorize
+ H=hill
+ hilk=function(k)
+ HilK\[s,\]=Vectorize
+ }
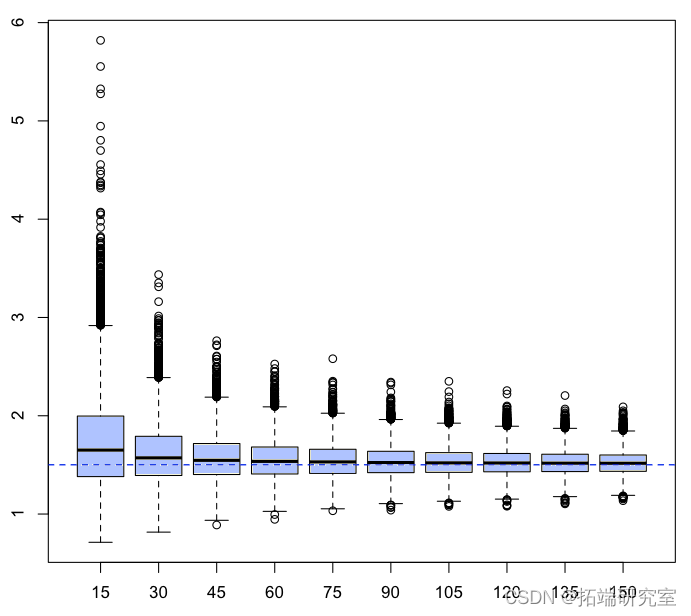
如果我们计算平均值，
> plot(15*(1:10),apply(2,mean)
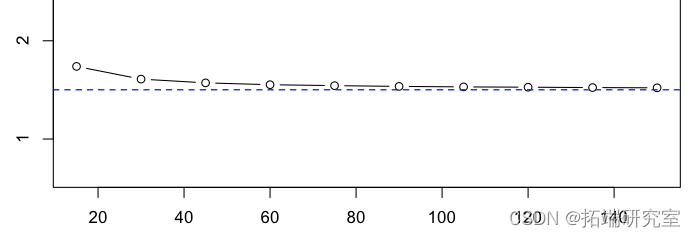
我们得到了一系列可以被认为是无偏的估计量。
现在，回想一下，处于 Fréchet 分布并不意味着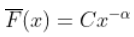 
， 和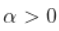 
, 但意味着
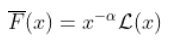
对于一些缓慢变化的函数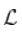 
，不一定恒定！为了了解可能发生的情况，我们必须稍微具体一些。这只能通过查看生存函数的性质。假设，这里有一些辅助函数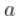 
随时关注您喜欢的主题
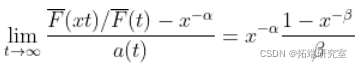
这个（正）常数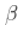 
以某种方式与生存函数与幂函数之比的收敛速度有关。
更具体地说，假设
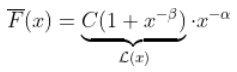
然后，使用获得二阶正则变化性质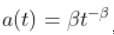 
，然后，如果 
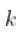趋向于无穷大太快，那么估计就会有偏差。 如果 
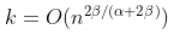，那么，对于一些 
,
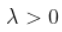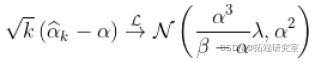
这个结果的直观解释是，如果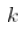 
太大，并且如果基础分布不_完全_ 是帕累托分布，那么希尔估计量是有偏的。这就是我们所说的意思
- 如果
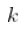太大，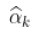 
是有偏估计量 - 如果
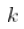太小，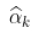 
是一个不稳定的估计量
（后者来自样本均值的属性：观察越多，均值的波动性越小）。
让我们运行一些模拟以更好地了解正在发生的事情。使用前面的代码，生成具有生存函数的随机样本实际上是极其简单的
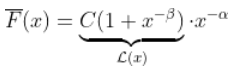
> Q=function(p){uniroot(function(x) S(x)-(1-p)}
如果我们使用上面的代码。
希尔hill变成
> abline(h=alpha)
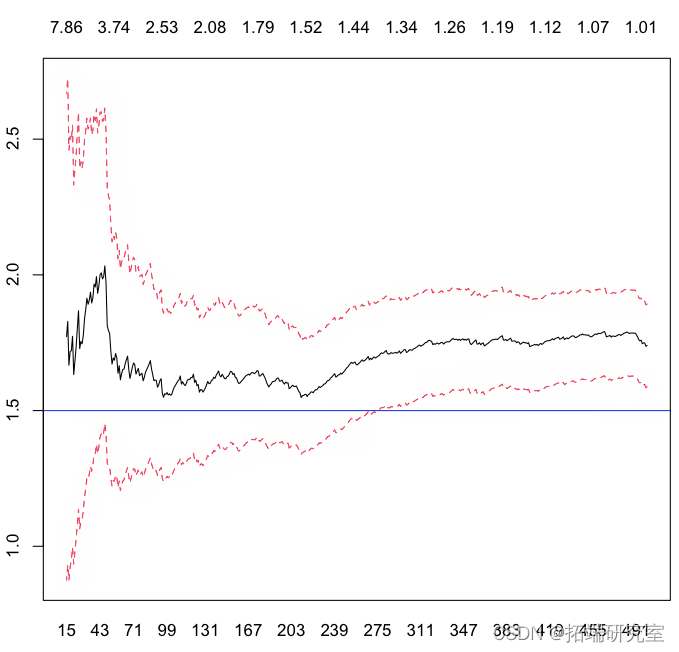
但它仅基于一个样本。再次考虑数千个样本，让我们看看 Hill 统计量如何，
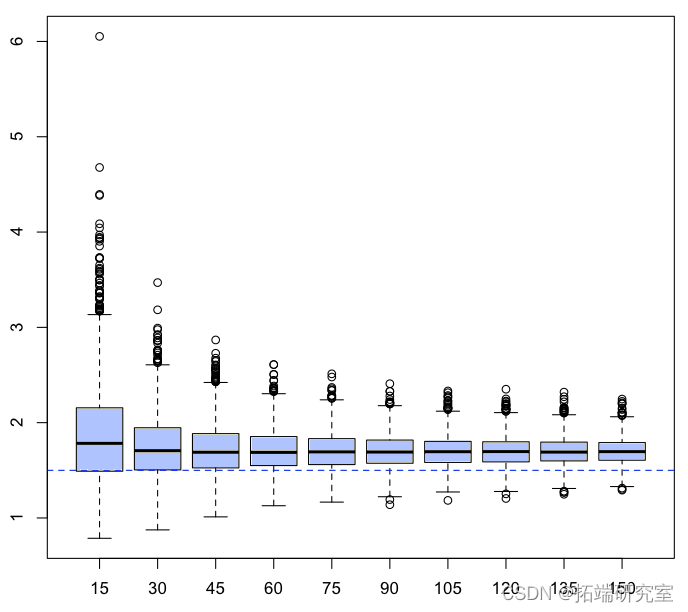
所以这些估计量的（经验）平均值是
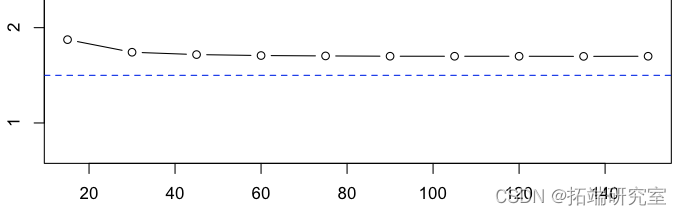
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素
r语言Bootstrap自助法重采样构建统计量T抽样分布近似值可视化
R语言门限误差修正模型(TVECM)参数估计沪深300指数和股指期货指数可视化
R语言Bootstrap、百分位Bootstrap法抽样参数估计置信区间分析通勤时间和学生锻炼数据
