马尔可夫链进行超过阈值的峰分析的经典方法是使GPD拟合最大值。但是，由于仅考虑群集最大值，因此存在数据浪费。
为了帮助客户使用POT模型，本指南包含有关使用此模型的实用示例。
本文快速介绍了极值理论（EVT）、一些基本示例，最后则通过案例对河流的极值进行了具体的统计分析。
可下载资源
EVT的介绍
单变量情况
假设存在归一化常数an> 0和bn使得：
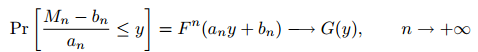
估计VaR有两类主要的方法，非参数（Nonparametric）方法和参数（parametric）方法。非参数方法基于历史收益率数据或者模拟收益率数据的分布，来获得对VaR的估计。参数方法则通过对于收益率随机变量的分布类型和参数做出估计，通过分布函数（概率密度函数）来对VaR做出估计。非参数方法由于样本数据的随机性以及尾部数据的稀少性，从而对于极端损失的估计不够精确。参数方法中的分布函数是对于全部收益率数据的一种数学概括，往往这种概括并不能很好地描述尾部的情况。作为对上述两类方法的结合，极值理论（Extreme Value Theory）以尾部（亏损）区域的收益率数据为基础，先估计出尾部数据的分布函数（概率密度函数），再利用分布函数对VaR做出估计。由于分布函数是基于尾部数据得到的，所以对于VaR的预测也更加地准确。
例如，收集从1960年到1987年10月16日期间的S&P 500指数的日收益率数据，然后找出每一年的最大的日亏损率数据，一共有28个数据点（极端亏损数据），其中最大的单日跌幅为6.7%。以Frechet分布来拟合28个亏损数据点，得到具体的分布函数。然后根据所得到的分布函数，可以求出置信水平为98%的VaR为24%，也就是说预计每50年里有1年会出现单日跌幅超过24%的情况，根据分布函数所预测的极端损失（24%）远远高于经验数据所反映的极端损失（6.7%）。在休市两天以后，1987年10月19日，美国股市崩溃，S&P 500指数单日跌幅超过20%。从中可以看到，极值理论对于尾部损失预测的可靠性较高。
极端亏损数据的采集方式有两种，一种称为Peaks over Threshold (POT)方法，另一种称为Block Maxima (BM)方法。POT方法选定一个门槛亏损率，然后将收益率经验数据中所有亏损幅度超过门槛收益率的数据保留下来，作为拟合尾部分布的数据基础。
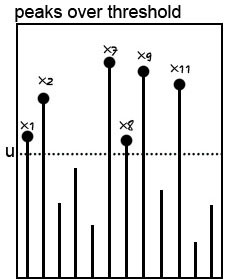
BM方法将所有的收益率数据根据时间顺序排列，并根据固定的间距分成许多组，然后从每一组中选出最大值（亏损为正数，收益为负数），将选出的数据点作为拟合尾部分布的数据基础。
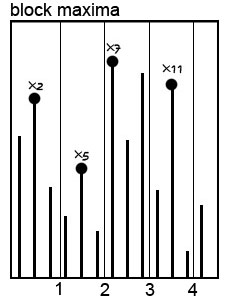
极端数据的采集方式不同，在此基础上拟合的分布类型也不同。POT方法采集的数据，用Generalized Pareto分布进行拟合； BM方法采集的数据，用Generalized Extreme Value分布来拟合。在分布参数的选择时，需要考虑到损失数据的肥尾现象。
根据极值类型定理（Fisher和Tippett，1928年），G必须是Fr’echet，Gumbel或负Weibull分布。Jenkinson（1955）指出，这三个分布可以合并为一个参数族：广义极值（GEV）分布。GEV具有以下定义的分布函数：
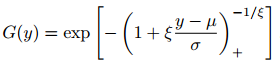
根据这一结果，Pickands（1975）指出，当阈值接近目标变量的端点µend时，阈值阈值的标准化超额的极限分布是广义Pareto分布（GPD）。也就是说，如果X是一个随机变量，则：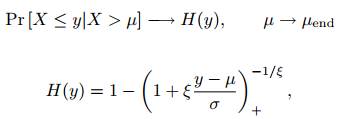
基本用法
随机数和分布函数
首先，让我们从基本的东西开始。将R用于随机数生成和分布函数。
> rgpd(5, loc = 1, scale = 2, shape = -0.2)
[1] 1.523393 2.946398 2.517602 1.199393 2.541937
> rgpd(6, c(1, -5), 2, -0.2)
[1] 1.3336965 -4.6504749 3.1366697 -0.9330325 3.5152161 -4.4851408
> rgpd(6, 0, c(2, 3), 0)
[1] 3.1139689 6.5900384 0.1886106 0.9797699 3.2638614 5.4755026
> pgpd(c(9, 15, 20), 1, 2, 0.25)
[1] 0.9375000 0.9825149 0.9922927
> qgpd(c(0.25, 0.5, 0.75), 1, 2, 0)
[1] 1.575364 2.386294 3.772589
> dgpd(c(9, 15, 20), 1, 2, 0.25)
[1] 0.015625000 0.003179117 0.001141829
使用选项lower.tail = TRUE或lower.tail = FALSE分别计算不超过或超过概率；
指定分位数是否超过概率分别带有选项lower.tail = TRUE或lower.tail = FALSE；
指定是分别使用选项log = FALSE还是log = TRUE计算密度或对数密度。
阈值选择图
此外，可以使用Fisher信息来计算置信区间。
> x <- runif(10000)
> par(mfrow = c(1, 2))结果如图所示。我们可以清楚地看到，将阈值设为0.98是合理的选择。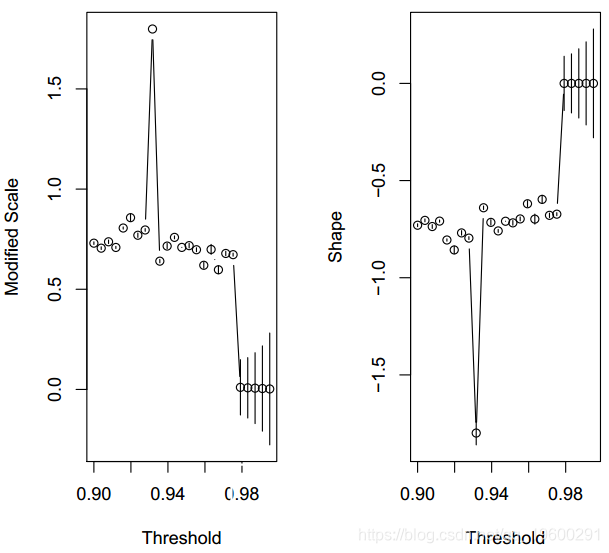
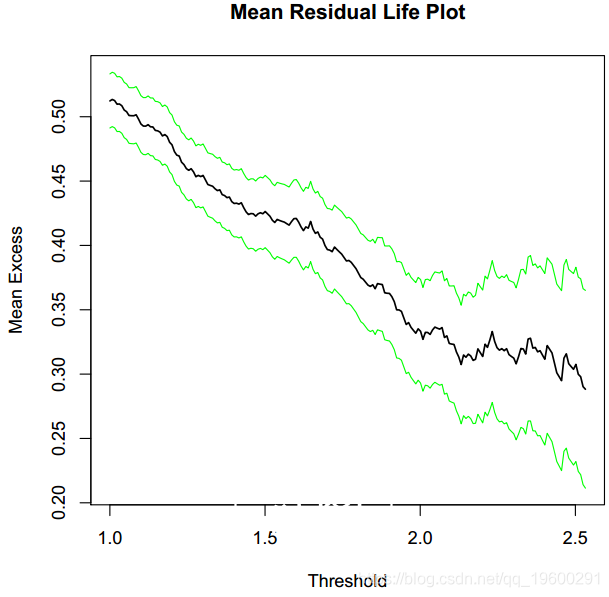
可以将置信区间添加到该图，因为经验均值可以被认为是正态分布的（中心极限定理）。但是，对于高阈值，正态性不再成立，此外，通过构造，该图始终会收敛到点（xmax; 0）。
这是另一个综合示例。
> x <- rnorm(10000)
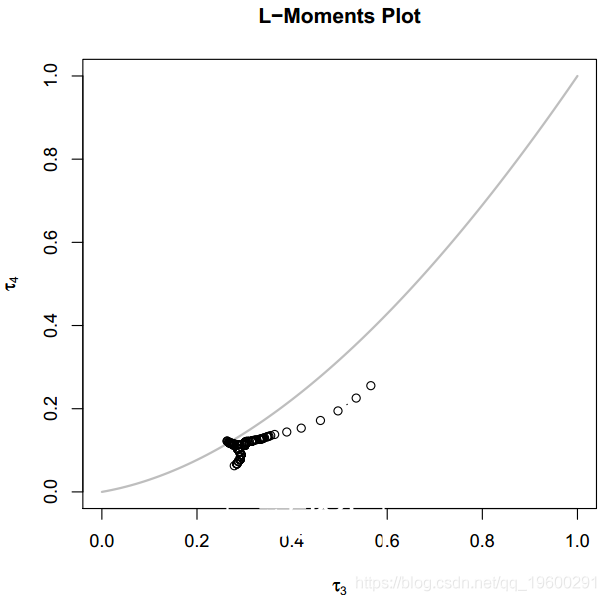
plot(x, u.range = c(1, quantile(x, probs = 0.995)), col = L-矩图
L-矩是概率分布和数据样本的摘要统计量。它们类似于普通矩{它们提供位置，离散度，偏度，峰度以及概率分布或数据样本形状的其他方面的度量值{但是是从有序数据值的线性组合中计算出来的（因此有前缀L）。
这是一个简单的例子。
> x <- c(1 - abs(rnorm(200, 0, 0.2)), rgpd(100, 1, 2, 0.25))
我们发现该图形在真实数据上的性能通常很差。
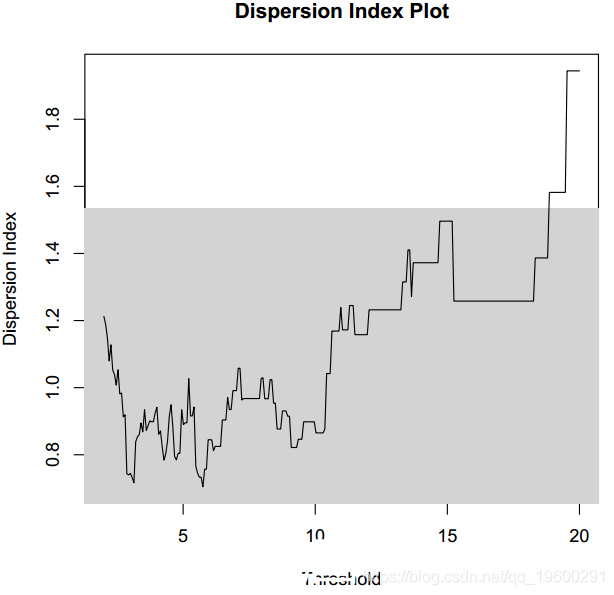
色散指数图
在处理时间序列时，色散指数图特别有用。EVT指出，超出阈值的超出部分可以通过GPD近似。但是，EVT必须通过泊松过程来表示这些超额部分的发生。
对于下一个示例，我们使用POT包中包含的数据集。此外，由于洪水数据是一个时间序列，因此具有很强的自相关性，因此我们必须“提取”极端事件，同时保持事件之间的独立性。
5, clust.max = TRUE)
> diplot(events, u.range = c(2, 20))随时关注您喜欢的主题
色散指数图如图所示。从该图可以看出，大约5的阈值是合理的。
拟合GPD
单变量情况
可以根据多个估算器拟合GPD。
MLE是一种特殊情况，因为它是唯一允许变化阈值的情况。
我们在此给出一些教学示例。
scale shape
mom 1.9538076495 0.2423393
mle 2.0345084386 0.2053905
pwmu 2.0517348996 0.2043644
pwmb 2.0624399910 0.2002131
pickands 2.3693985422 -0.0708419
med 2.2194363549 0.1537701
mdpd 2.0732577511 0.1809110
mple 2.0499646631 0.1960452
ad2r 0.0005539296 27.5964097
MLE，MPLE和MGF估计允许比例或形状参数。例如，如果我们要拟合指数分布：
> fit(x, thresh = 1, shape = 0, est = "mle")
Estimator: MLE
Deviance: 322.686
AIC: 324.686
Varying Threshold: FALSE
Threshold Call: 1
Number Above: 100
Proportion Above: 1
Estimates
scale
1.847
Standard Error Type: observed
Standard Errors
scale
0.1847
Asymptotic Variance Covariance
scale
scale 0.03410
Optimization Information
Convergence: successful
Function Evaluations: 7
Gradient Evaluations: 1
> fitgpd(x, thresh = 1, scale = 2, est = "mle")
Estimator: MLE
Deviance: 323.3049
AIC: 325.3049
Varying Threshold: FALSE
Threshold Call: 1
Number Above: 100
Proportion Above: 1
Estimates
shape
0.0003398
Standard Error Type: observed
Standard Errors
shape
0.06685
Asymptotic Variance Covariance
shape
shape 0.004469
Optimization Information
Convergence: successful
Function Evaluations: 5
Gradient Evaluations: 1
If now, we want to fit a GPD with a varying threshold, just do:
> x <- rgpd(500, 1:2, 0.3, 0.01)
> fitgpd(x, 1:2, est = "mle")
Estimator: MLE
Deviance: -176.1669
AIC: -172.1669
Varying Threshold: TRUE
Threshold Call: 1:2
Number Above: 500
Proportion Above: 1
Estimates
scale shape
0.3261 -0.0556
Standard Error Type: observed
Standard Errors
scale shape
0.02098 0.04632
Asymptotic Variance Covariance
scale shape
scale 0.0004401 -0.0007338
shape -0.0007338 0.0021451
Optimization Information
Convergence: successful
Function Evaluations: 62
Gradient Evaluations: 11| scale1 | shape1 | scale2 | shape2 | α |
| 6.784e-02 | 5.303e-02 | 2.993e-02 | 3.718e-02 | 2.001e-06 |
Asymptotic Variance Covariance
scale1 shape1 scale2 shape2 alpha
scale1 4.602e-03 -2.285e-03 1.520e-06 -1.145e-06 -3.074e-11
shape1 -2.285e-03 2.812e-03 -1.337e-07 4.294e-07 -1.843e-11
scale2 1.520e-06 -1.337e-07 8.956e-04 -9.319e-04 8.209e-12
shape2 -1.145e-06 4.294e-07 -9.319e-04 1.382e-03 5.203e-12
alpha -3.074e-11 -1.843e-11 8.209e-12 5.203e-12 4.003e-12
Optimization Information
Convergence: successful
Function Evaluations: 150
Gradient Evaluations: 21拟合双变量POT。所有这些模型均使用最大似然估计量进行拟合。
双变量情况
vgpd(cbind(x, y), c(0, 2), model = "log")
> Mlog
Estimator: MLE
Dependence Model and Strenght:
Model : Logistic
lim_u Pr[ X_1 > u | X_2 > u] = NA
Deviance: 1313.260
AIC: 1323.260
Marginal Threshold: 0 2
Marginal Number Above: 500 500
Marginal Proportion Above: 1 1
Joint Number Above: 500
Joint Proportion Above: 1
Number of events such as {Y1 > u1} U {Y2 > u2}: 500
Estimates
scale1 shape1 scale2 shape2 alpha
0.9814 0.2357 0.5294 -0.2835 0.9993
Standard Errors
在摘要中，我们可以看到lim_u Pr [X_1> u | X_2> u] = 0.02。这是Coles等人的χ统计量。（1999）。对于参数模型，我们有：
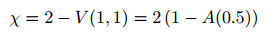
对于自变量，χ= 0，而对于完全依存关系，χ=1。在我们的应用中，值0.02表示变量是独立的{这是显而易见的。从这个角度来看，可以固定一些参数。
vgpd(cbind(x, y), c(0, 2), model = "log"
Dependence Model and Strenght:
Model : Logistic
lim_u Pr[ X_1 > u | X_2 > u] = NA
Deviance: 1312.842
AIC: 1320.842
Marginal Threshold: 0 2
Marginal Number Above: 500 500
Marginal Proportion Above: 1 1
Joint Number Above: 500
Joint Proportion Above: 1
Number of events such as {Y1 > u1} U {Y2 > u2}: 500
Estimates
scale1 shape1 scale2 shape2
0.9972 0.2453 0.5252 -0.2857
Standard Errors
scale1 shape1 scale2 shape2
0.07058 0.05595 0.02903 0.03490
Asymptotic Variance Covariance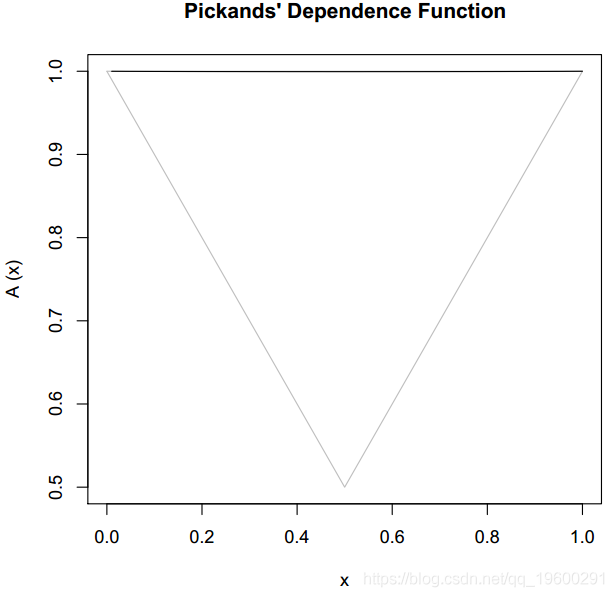
scale1 shape1 scale2 shape2
scale1 4.982e-03 -2.512e-03 -3.004e-13 3.544e-13
shape1 -2.512e-03 3.130e-03 1.961e-13 -2.239e-13
scale2 -3.004e-13 1.961e-13 8.427e-04 -8.542e-04
shape2 3.544e-13 -2.239e-13 -8.542e-04 1.218e-03
Optimization Information
Convergence: successful
Function Evaluations: 35
Gradient Evaluations: 9
注意，由于所有双变量极值分布都渐近相关，因此Coles等人的χ统计量。（1999）始终等于1。
检测依赖强度的另一种方法是绘制Pickands的依赖函数：
> pickdep(Mlog)
水平线对应于独立性，而其他水平线对应于完全相关性。请注意，通过构造，混合模型和非对称混合模型无法对完美的依赖度变量建模。
使用马尔可夫链对依赖关系结构进行建模
马尔可夫链进行超过阈值的峰分析的经典方法是使GPD拟合最大值。但是，由于仅考虑群集最大值，因此存在数据浪费。本文主要思想是使用马尔可夫链对依赖关系结构进行建模，而联合分布显然是多元极值分布。这个想法是史密斯等人首先提出的（1997）。在本节的其余部分，我们将只关注一阶马尔可夫链。因此，所有超出的可能性为：
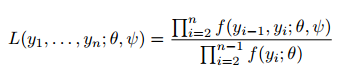
对于我们的应用程序，我们模拟具有极值依赖结构的一阶马尔可夫链。
mcgpd(mc, 2, "log")
Estimator: MLE
Dependence Model and Strenght:
Model : Logistic
lim_u Pr[ X_1 > u | X_2 > u] = NA
Deviance: 1334.847
AIC: 1340.847
Threshold Call:
Number Above: 998
Proportion Above: 1
Estimates
scale shape alpha
0.8723 0.1400 0.5227
Standard Errors
scale shape alpha
0.08291 0.04730 0.02345
Asymptotic Variance Covariance
scale shape alpha
scale 0.0068737 -0.0016808 -0.0009066
shape -0.0016808 0.0022369 -0.0004412
alpha -0.0009066 -0.0004412 0.0005501
Optimization Information
Convergence: successful
Function Evaluations: 70
Gradient Evaluations: 15置信区间
拟合统计模型后，通常会给出置信区间。当前，只有mle，pwmu，pwmb，矩估计量可以计算置信区间。
conf.inf.scale conf.sup.scale
2.110881 2.939282
conf.inf.scale conf.sup.scale
1.633362 3.126838
conf.inf.scale conf.sup.scale
2.138851 3.074945
conf.inf.scale conf.sup.scale
2.149123 3.089090
对于形状参数置信区间：
conf.inf conf.sup
2.141919 NAconf.inf conf.sup
0.05757576 0.26363636
分位数的置信区间也可用。
conf.inf conf.sup
2.141919 NAconf.inf conf.sup
0.05757576 0.26363636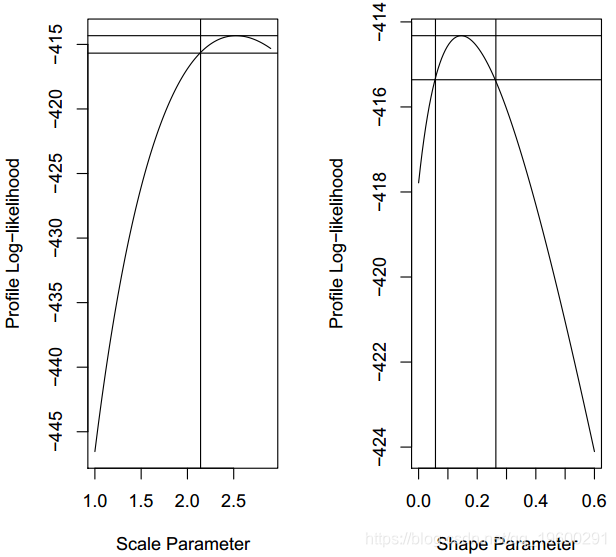
conf.inf conf.sup
8.64712 12.22558conf.inf conf.sup
8.944444 12.833333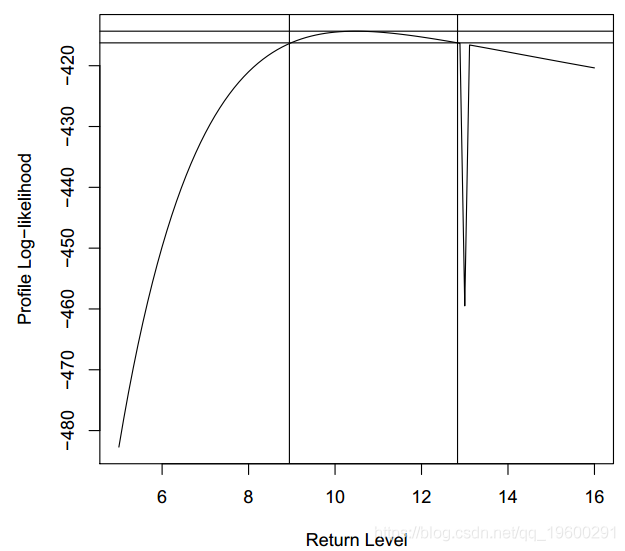
conf.inf conf.sup
8.64712 12.22558conf.inf conf.sup
8.944444 12.833333
轮廓置信区间函数既返回置信区间，又绘制轮廓对数似然函数。
模型检查
要检查拟合的模型，用户必须调用函数图。
> plot(fitted, npy = 1)
图显示了执行获得的图形窗口。
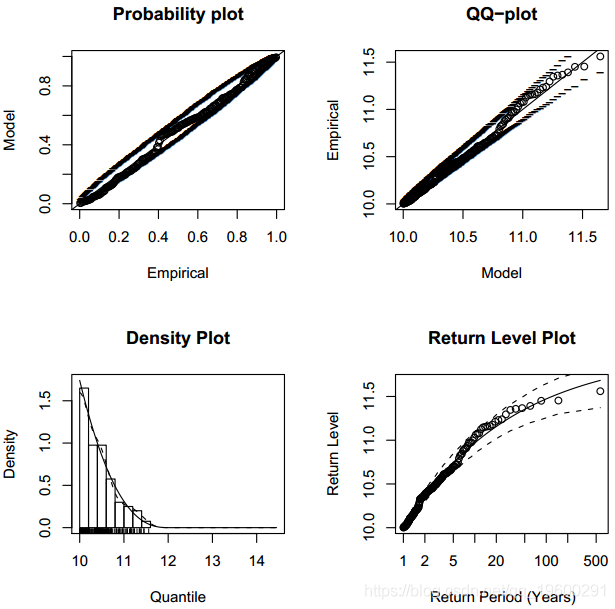
聚类技术
在处理时间序列时，超过阈值的峰值可能会出现问题。确实，由于时间序列通常是高度自相关的，因此选择高于阈值可能会导致相关事件。
该函数试图在满足独立性标准的同时识别超过阈值的峰。为此，该函数至少需要两个参数：阈值u和独立性的时间条件。群集标识如下：
1.第一次超出会启动第一个集群；
2.在阈值以下的第一个观察结果将“终止集群”，除非tim.cond不成立；
3.下一个超过tim.cond的集群将启动新集群；
4.根据需要进行迭代。
一项初步研究表明，如果两个洪水事件不在8天之内，则可以认为两个洪水事件是独立的，请注意，定义tim.cond的单位必须与所分析的数据相同。
返回一个包含已识别集群的列表。
clu(dat, u = 2, tim.cond = 8/365)
其他
返回周期
将返回周期转换为非超出概率，反之亦然。它既需要返回期，也需要非超越概率。此外，必须指定每年平均事件数。
npy retper prob
1 1.8 50 0.9888889
npy retper prob
1 2.2 1.136364 0.6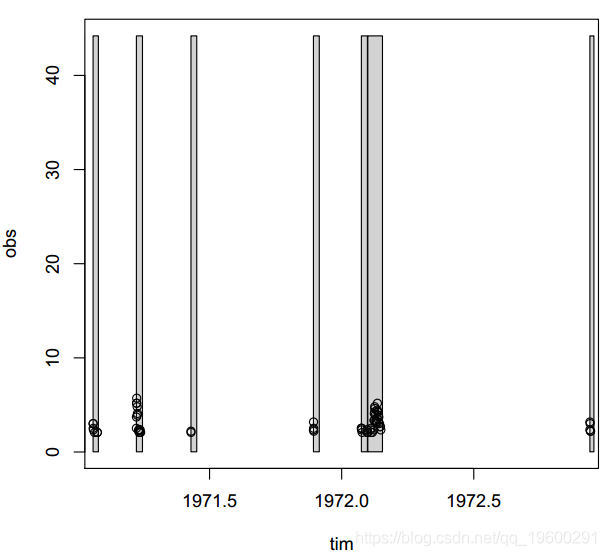
无偏样本L矩
函数samlmu计算无偏样本L矩。
l_1 | l_2 | t_3 | t_4 | t_5 |
| 0.455381591 | 0.170423740 | 0.043928262 -0.005645249 -0.009310069 | ||
| 3.7.3 |
河流阈值分析
在本节中，我们提供了对河流阈值的全面和详细的分析。
时间序列的移动平均窗口
从初始时间序列ts计算“平均”时间序列。这是通过在初始时间序列上使用长度为d的移动平均窗口来实现的。
> plot(dat, type = "l", col = "blue")> lines(tsd, col = "green")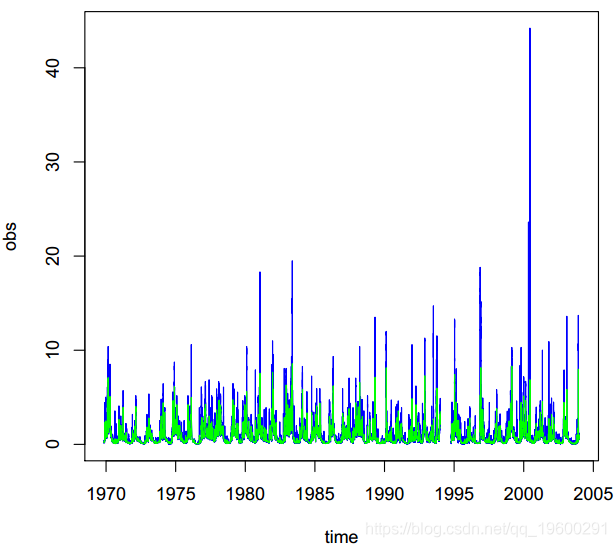
执行过程如图所示。图描绘了瞬时洪水数量-蓝线。
由于这是一个时间序列，因此我们必须选择一个阈值以上的独立事件。首先，我们固定一个相对较低的阈值以“提取”更多事件。因此，其中一些不是极端事件而是常规事件。这对于为GPD的渐近逼近选择一个合理的阈值是必要的。
> par(mfrow = c(2, 2))
> plot(even[, "obs"])
> abline(v = 6, col = "green"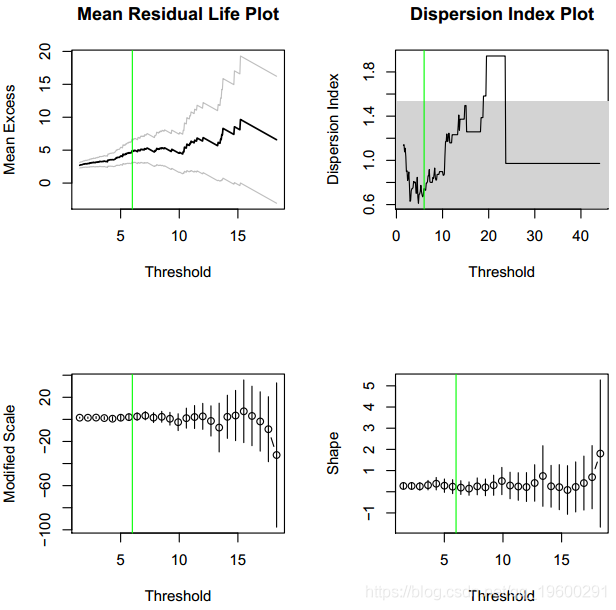
根据图，阈值6m3 = s应该是合理的。平均剩余寿命图-左上方面板-表示大约10m3 = s的阈值应足够。但是，所选阈值必须足够低，以使其上方具有足够的事件以减小方差，而所选阈值则不能过低，因为它会增加偏差3。
因此，我们现在可以\重新提取阈值6m3 = s以上的事件，以获得对象event1。注意，可以使用极值指数的估计。
> events1 <-365, clust.max = TRUE)
> np
time obs
Min. :1970 Min. : 0.022
1st Qu.:1981 1st Qu.: 0.236
Median :1991 Median : 0.542
Mean :1989 Mean : 1.024
3rd Qu.:1997 3rd Qu.: 1.230
Max. :2004 Max. :44.200
NA's : 1.000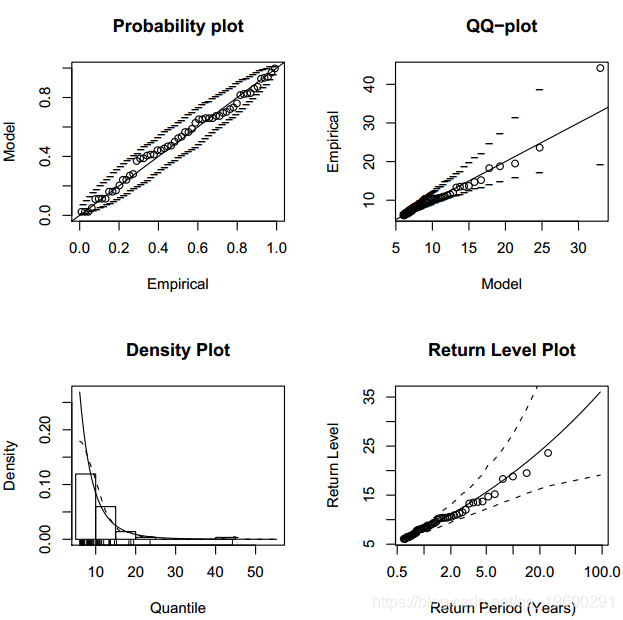
结果给出了估计器的名称（阈值，阈值以上的观测值的数量和比例，参数估计，标准误差估计和类型，渐近方差-协方差矩阵和收敛性诊断。
图显示了拟合模型的图形诊断。可以看出，拟合模型“ mle”似乎是合适的。假设我们想知道与100年返回期相关的返回水平。
> rp2pnpy retper prob1 1.707897 100 0.9941448> scale36.44331考虑到不确定性，图描绘了与100年返回期相关的分位数的分布置信区间。
conf.inf conf.sup25.56533 90.76633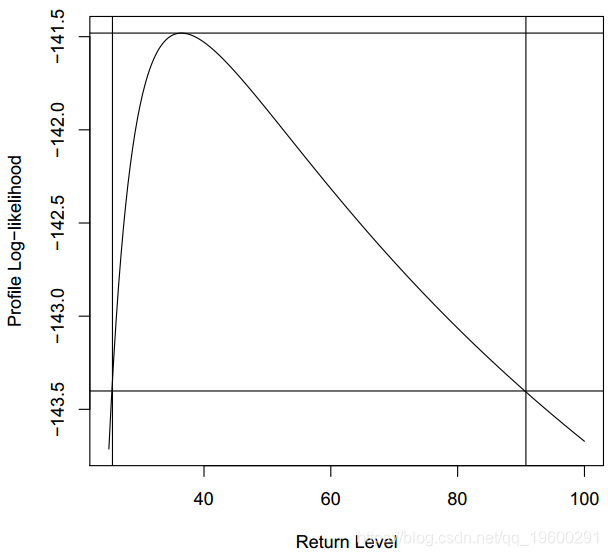
有时有必要知道指定事件的估计返回周期。让我们对较大事件进行处理。
> maxEvent[1] 44.2 shape0.9974115> probnpy retper prob1 1.707897 226.1982 0.9974115
因此，2000年6月发生的最大事件的重现期大约为240年。
conf.inf conf.sup25.56533 90.76633可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言极值分析：GEV与GPD模型与MCMC的海洋观测数据极值模拟可视化研究
多状态马尔可夫链、生存分析心脏同种异体移植血管病变（CAV）数据可视化|附数据代码
R语言离散时间马尔可夫链（Markov chain）模型分类案例可视化分析
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
