今天早上,我们使用一些论文中提到的示例,使用最大流最小割定理将流量拥塞降至最低, 并应用了最短路径分析了交通瓶颈。
在当今城市化进程不断加速的时代,城市交通拥堵已成为困扰人们生活和经济发展的一大难题。
随着城市人口的急剧增长和机动车保有量的持续攀升,交通网络承受着前所未有的压力。
交通拥堵不仅导致人们的出行时间大幅增加、生活质量下降,还会对城市的经济效率、环境质量产生负面影响。
如何有效地分析和解决交通网络流量拥堵问题,成为了城市规划者、交通管理者以及相关研究人员亟待解决的重要课题。
我们可以在下面看到
map=openp(map)
plot(map)
points(t(m[3:2,]),col="black", pch=19, cex=3提取有关边缘容量
要提取有关边缘容量的信息,在该网络上使用以下代码,该代码将从论文中提取三个表
extract_tab(location)在Windows中,要先下载另一个软件包
library(devtools)
extract_tab(locatio现在我们可以得出具有容量的数据框
B1=as.data.frame(out[[2]])
B2=as.data.frame(out[[3
capacity=as.character(B2$V3[-1])
capacity[6]="843"
ic(capacity)我们可以在地图上添加这些边
plot(map)
points(t(m[3:2,]),col="black", pch=1
for(i in 1:nrow(E)){
i1=which(B$i==as.character(E$from
]))
segments(B[i1,"x"],B[i1,"y"],B[i2,
text(t(m[3:2,]),c("s",1:10,"t"),col="white")要获得具有容量的图形,可以使用另一种方法
有容量的网络
g=graph_from_data_frame(E)
E(g)$label=E$capacity
plot(g)但是它不考虑节点的地理位置。可以使用
plot(g, layout=as.matrix(B[,c("x","y")]))
为了更好地了解道路通行能力,使用
plot(g, layout=as.matrix(B[,c("x","y")]),
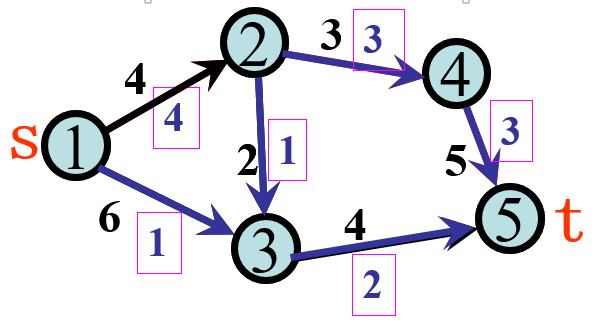
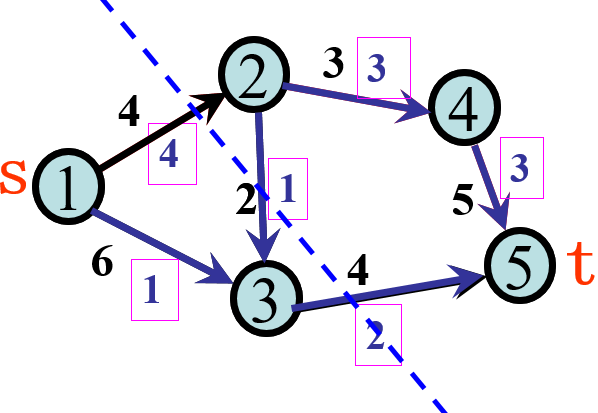
edge.width=E$capacity/200)通过具有容量的网络,目标是确定该网络上从源到宿的最大流量。可以使用R
$value
[1] 2571
$flow
[1] 10 142 130 23 0 2我们的最大流量为2571,这与两篇论文中的最大流量最小割定理以及 最短路径的应用中都实际要求的不同 ,因为表格和图表上的值不同。
E$flux1=m$flow
plot(g, layout=as.matrix(B[,c("x","y")]),考虑采用更简单的流程,但是相同的全局值
E(g)$label=E$flux2
plot(g, layout=as.matrix(B[,c("x","y")]),
edge.width=E$flux2/200)实际上,有可能在同一城市的另一篇论文中做同样的事情,这是道路网络的交通拥堵问题。
dim(out[[3]])
B1=a
ame(from=B1[2:61,"V2"],
to=B1[2:6
as.numeric(
as.characte
data_frame(E)
m=max_flow(graph=g,
source="S",
E$flux1=m$flow
E(g)$label=E
edge.width=E$flux1/200,
edge.arrow.size=0.15)此处的最大流量值为4017,就像原始论文中发现的那样
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析
视频讲解|Stata和R语言自助法Bootstrap结合GARCH对sp500收益率数据分析 高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据
高维变量选择专题|R、Python用HOLP、Lasso、SCAD、PCR、ElasticNet实例合集分析企业财务、糖尿病、基因数据 【专题】DeepSeek技术颠覆or创新共赢,开启Al算法变革元年报告汇总PDF洞察(附原数据表)
【专题】DeepSeek技术颠覆or创新共赢,开启Al算法变革元年报告汇总PDF洞察(附原数据表) 【视频】因子分析简介及R语言应用实例:对地区经济研究分析重庆市经济指标
【视频】因子分析简介及R语言应用实例:对地区经济研究分析重庆市经济指标



