从广义上讲，复杂的模型可以实现很高的预测准确性。
但是您的读者需要快速理解。他们没有意愿或时间去处理任何太乏味的事情，即使它可以稍微准确一些。
简单性是商业中非常重要的模型选择标准。在多元波动率估计中，最简单的方法是使用历史协方差矩阵。
可下载资源
但这太简单了，我们已经知道波动性是随时间变化的。您经常看到从业者使用滚动标准差来模拟随时间变化的波动率。
它可能不如其他最先进的方法准确， 但它实现起来非常简单，也很容易解释。
什么是滚动窗口估计。如果我们有一个包含 5 个观察值的向量并且我们使用 2 个窗口，那么用于估计的权重向量是 [0,0,0,0.5,0.5]。更进一步的做法是对更远的过去给予少一些权重，但要对最近的观察样本给予更大的权重，比如权重向量 [0.05, 0.1, 0.15, 0.3, 0.4]。
根据低波动率跟着低波动率走，高波动率跟着高波动率走（波动率聚类）的典型事实，这个想法完全适合于多变量波动率预测。请考虑以下情况。
(1) 
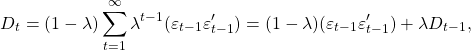
其中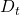 
是协方差矩阵的当前估计，并且 
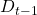是基于过去直到时间段 t-1 的协方差矩阵。我们使用最简单的估计，即历史协方差矩阵，但增加了一些权重（
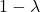）到仅基于最近的观察估计的协方差矩阵。这真的很容易解释，几乎是一个行业标准。可以估计我们希望权重下降的速度，但您也可以根据一些先前的研究，将衰减参数估计为 0.94。
我绘制几个不同 lambda 值随时间变化的相关矩阵：
k <- 10 # 几年前？
end<- format(Sys.Date(),"%Y-%m-%d")
start<-format(Sys.Date() - (k*365),"%Y-%m-%d")
dat0 = getSymbols
for (i in 1:l){
da0 = getSymbols(sym\[i\])
ret\[2:n,i\]
}
EWMAplot
legend
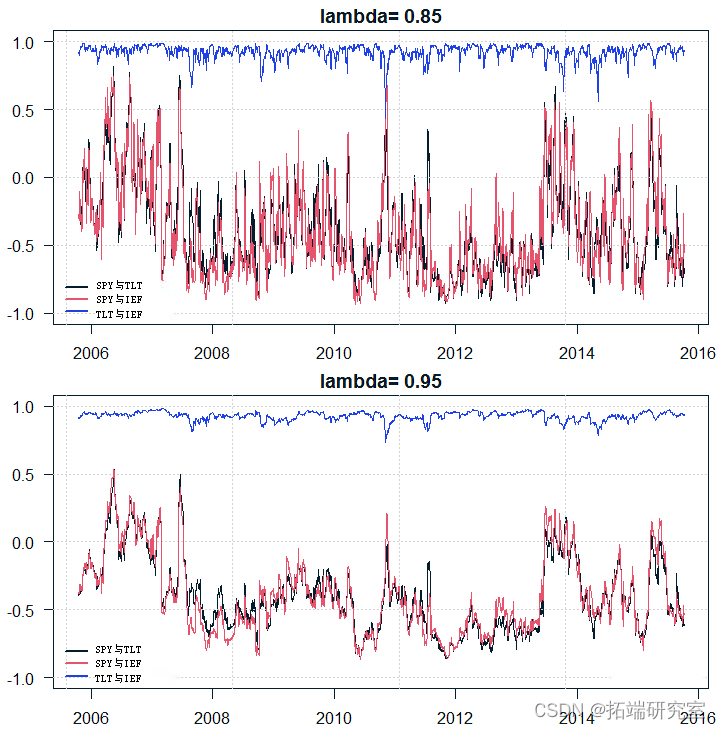
您可以看到，如果您为最后一次观察样本分配 15% 的权重，您会得到一些不稳定的估计。仅 5% (lambda = 0.95) 的权重给出了更平滑的估计，但可能不太准确。
除了简单之外，另一个重要的优点是不需要关心可逆性，因为在每个时间点上，估计值只是两个有效的相关矩阵的加权平均数。还有，你可以将这种方法应用于任何金融工具，不管是流动的还是非流动的，这是它受欢迎的另一个原因。
EWMA <-
function {
## ＃＃＃输入。
## factors N x K的数字因素数据。数据是类data.frame
## N是时间长度，K是因素的数量。
## lambda 标量。指数衰减系数在0和1之间。
## return.cor 如果是TRUE则返回EWMA相关矩阵
##输出。
covewma = array
covf = var(factors) # 时间=0时的无条件方差为EWMA
mfas <- apply(factors,2, mean)
for (i in 2:t.factor) {
FF
cov.f.ewma
}
}
if(return.cor) {
cewma
for (i in 1:dim\[1\]) {
corewma= covr(coewm\[i, ,\])
随时关注您喜欢的主题
这个函数不适合用于样本外的预测。原因是我们向样本协方差矩阵收缩，而协方差矩阵是基于全样本的，在样本结束前我们还不知道。在现实的设置中，我们只能使用到我们希望预测的那一点为止的信息。随后，我改变了原始函数，加入了一个额外的参数（用于估计协方差矩阵的初始窗口长度）。然后，初始协方差矩阵的取值只使用到预测时为止的信息，标准化也是如此。修改后的新函数如下
EWMAs <- function{
# 调整了样本外的协方差预测
## 输入。
##因素N x K数字因素数据。数据是类data.frame
## N是时间长度，K是因素的数量。
## la指数衰减因子在0和1之间。
## retu 逻辑的，如果是TRUE则返回EWMA相关矩阵
##输出。
coa = array(,c(t.cor,k.tor,k.aor))
fas <- apply
covf = var
co.ewa\[(wind-1),,\] = (1-lad)\*FF + ada\*cov.f
for (i in wind : t.factor) {
covf = var# 到t的无条件方差。
FF = (fators\[i,\]- mctors) %*% t(factors\[i,\]- mfcrs)
coma\[i,,\] = (1-laa)\*FF + laba\*coma\[(i-1),,\]
for (i in wn:dim) {
orma\[i, , \] = covr(owma\[i, ,\])
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
R语言股价跳跃点识别：隐马尔可夫hmm和GARCH-Jump对sp500金融时间序列分析
【视频讲解】Python用LSTM长短期记忆网络GARCH对SPX指数金融时间序列波动率滚动预测
【视频讲解】滚动回归Rolling Regression、ARIMAX时间序列预测Python、R实现应用
