
我们被客户要求使用R库mgcv,用广义加性模型(GAMs)对环境数据进行建模。
mgcv是一个伟大的库,具有丰富的功能,但我们经常发现,默认的诊断图并不令人振奋。
特别是偏残差图,功能很强,但不漂亮,残差几乎看不见。我们需要根据这些代码来制作自己的偏回归平滑图。
可下载资源
1) 基本的数据设置
我们正在使用这里讨论的数据集。我们使用的是国家发病率和死亡率空气污染研究(NMMAPS)的数据。我们将数据限制在1997-2000年。
我们介绍一些由线性假设下,扩展得到的其他模型。
一,多项式回归
在了解简单线性模型的基础上,很容易理解多项式回归,形如:
yi=β0+β1x11+β2x22+...++βnxnn+ei
其中,
ei
为误差项
多项式回归的优点是,随着变量的增加,可以拟合出异常极端变化的曲线。不过通常来说,多项式回归基本都不会超过四项式。
多项式也可以结合logistics进行回归,形如:
P(yi|xi)=exp(β0+β1x11+β2x22+...++βnxnn)1+exp(β0+β1x11+β2x22+...++βnxnn)
二,分段常值函数(step functions)
不论简单线性回归、多项式回归等都是具有全局性的结构。再不考虑全局性回归时,可以用到分段回归。
最简单的分段回归应该就是形如阶跃函数了,阶跃函数也是提供连续变量离散化成有序分类变量的方法。
过程如下:
对X进行分组;
每个组拟合出不同的常量;
假设对X有K个截点,
c1,c2,...,ck
我们生成K+1个新变量: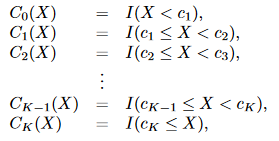
这些变量有时候也叫虚拟变量或哑变量,然后对这K+1个变量进行拟合,得到形如: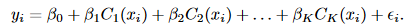
三,基底函数(basis functions)
前两种回归方式,都可以总结为是基底函数的特例。所谓的基底函数是不直接对X进行回归,而是用函数函数变化后的 bi(xi) 值进行回归,形如:
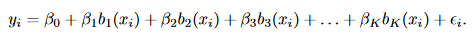
当
bj(xi)=xji
时,就变成了多项式回归;
当
bj(xi)=I(cj≤xi<cj+1)
时,就变成了分段回归;
四,回归样条(Regression Splines)
由基底函数可知,基函数可以是任意的组合形式,不过接下来我们介绍的一种基函数是结合了多项式和分段常值函数的”回归样条”.
什么是样条呢?
样条是一个函数,由多项式构造的分段函数,并且在分段节点处要具有高度平滑的特性,即在分段结点处连续且有连续的导数。
1,三次样条:
一个三次多项式分段回归如下,但是该回归并不满足”平滑的特性”,在结点处可能出现跳跃。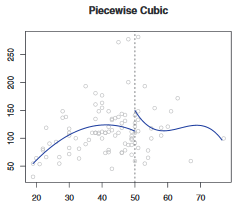
所以,我们要加两个限制条件,让其变成一个样条回归:
1)结点处连续;
2)结点处平滑;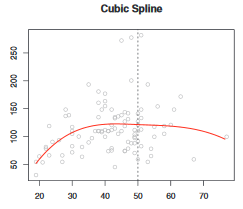
定义,K个节点下的三次样条回归模型: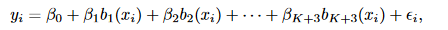
三次样条下,基函数
b()
也有非常多的选择,最直接的方法就是对
X,X2,X3,h(X,ξ1),h(X,ξ2),...,h(X,ξK)
,进行拟合
其中,
ξi
是结点: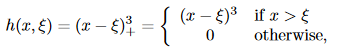
样条缺点是,有时候受异常点影响较大。需要加上额外的边界约束。
2,如何确定结点的个数与位置
一种方法是在变化相对稳定的区间设置尽量少的结点,在变化相对快速的地方设置尽量多的结点。尽量让每个结点区间内的变量趋于均匀分布。
另一种方法是设置自由度,根据算法自动跑出最优的结点位置。
自由度的个数可以结合交叉验证来验证。
3,与多项式回归的比较
由于样条有结点的帮助,所以在变动很大的数据背景下,仍然可以保证多项式的次数较小。而多项式回归则可能需要更多的次数(如 X15 ) 。一句话概括即是样条比多项式回归更灵活。
4,平滑样条曲线
假设我们样条函数为g(x),再求得该函数参数的同时,如何保证样条曲线的平滑性呢?
结合第四章所讲,在求解样条回归的结构风险最小化(RSS+惩罚项)时,把惩罚项设置为”平滑性”相关的表示,形如: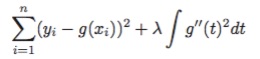
函数在某点处的一阶导数表示的该点曲线的斜率,二阶导数表示的就是斜率的变化率,即,惩罚项即表示为函数曲线在该点的平滑性。
但是,在一段区间内,曲线整体的平滑性要如何衡量呢?我们用到了 ∫ 。上式中的惩罚项表示为对区间t内,一阶导数 g′(t) 累计的变化情况,因此可以用来衡量该段区间整体的平滑性了。
超参λ,则是用来衡量惩罚项的重要性占比的。一般用n折交叉验证或者留一交叉验证法来确定。
五,局部回归(Local Regression)
局部回归是另一种拟合非线性模型的方法。
为了实现局部回归,有许多重要步骤需要确定:
– 确定加权函数K
– 确定局部回归的模型:线性/二次/还是常数等,通常是简单模型
– 最重要的还是对“局部”的定义,如何确定点
x0
点近临范围“s”
范围s的值越小,每次拟合的数据区间越小,并且到下一个拟合点到距离也越小。我们可以用交叉验证的方法来确定s,或者人为设定一个值。
1)最简单的局部模型
局部平均(local average)模型是最简单的局部模型,形如: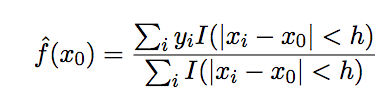
其缺点是,估计结果并非是连续的。
且与KNN的思想类似,是一种非参数方法。
2)Nadaraya-Watson 核估计(NW)
引用核估计方法,将local average模型进行改造,当K是连续时,f即为连续的。
其局部性参数h可以通过交叉验证的方式计算得到。
不过当x不是均匀分布的时候,该方法将产生偏倚。
3)lowess
前两种方法都属于非参数方法,下面介绍一种结合了非参和参数模型的方法:lowess或者又叫做loess,通过对局部进行线性拟合(非常数值拟合),来解决NW的缺点。
lowess 算法:
1)给定数据集
D=(xi,yi)
, 核函数K(),
2)拟合局部回归
w^(x)=argmin∑ni=1K(x,xi)∗(wTxi−yi)2
3)得到拟合结果
w^(x)Tx
局部加权logistics回归算法:
1)给定数据集
D=(xi,yi)
, 核函数K(),
2)拟合局部回归
w^(x)=argmin∑ni=1K(x,xi)∗log(1+exp(−yiwTxi))
3)得到拟合结果
sign(w^(x)Tx)
总结:
六,广义相加模型(Generalized Additive Models)
前面,我们已经介绍了一些方法,作为简单线性模型的扩展。这些方法可以归纳为广义相加模型(GAMs)的框架里,形如: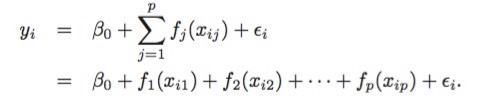
之所是”相加性的”,是因为我们对于每个变量 Xj 都单独计算 fj , fj 可以是任意形式的函数,最后统一加起来用来预测 Y .
GAMs的优缺点:
– 可以引入非线性函数
fj
– 非线性可能使得对Y预测的更准确
– 因为是”相加性的”,所以,线性模型的假设检验的方法仍然可以使用
– 因为是“相加性”假设,所以GAMs中可能会缺失重要的交互作用
Xj×Xk
,只能通过手动添加交互项来弥补。
v
data\[date>as.Date("1996-12-31"),\]
2) 简单的GAM模型–温度对臭氧
在这个例子中,我们保持模型的简单性–使用高斯数据,单一预测因子。我们对温度与臭氧进行建模,我们将输出默认的偏残差图。
# 模型 - 温度对臭氧的影响 plot(gam)
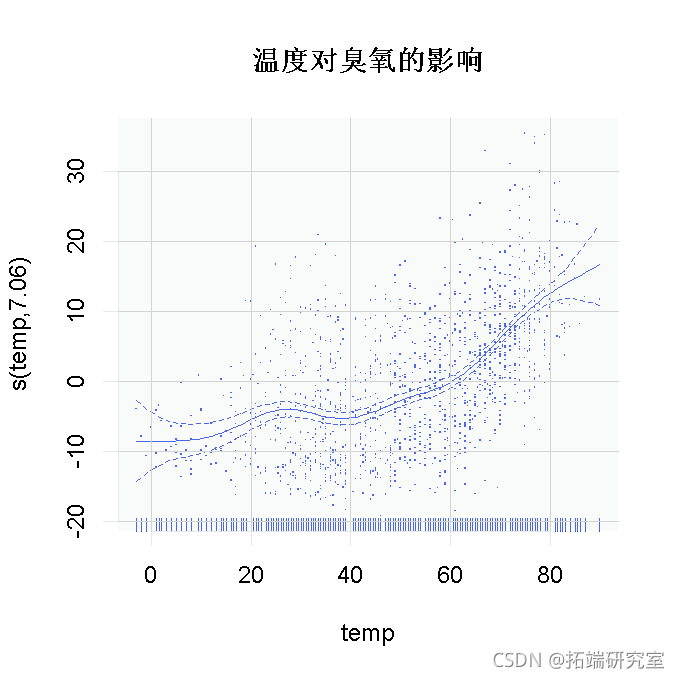
这个图可以改进?
3) 重新制作偏残差图
偏残差图(_Partial Residual_ Plot)是多元回归中常用的诊断工具,特别是评估模型中在一个或另一个解释变量中是否包含非线性项。在多元回归y=β0+β1×1+…+βpxp+ε中,若欲反映其中变量Xj与因变量y之间的关系并用图形显示,其方法之一是用偏残差图。
在这里,我们加入平滑项、置信区间和偏残差。
#我们可以在多边形的顶部添加线条 qplot(temp, fit, type="n")+poly(c(temp, rev(temp)), c(low95,rev(up95))# 对于置信度的灰色多边形
在最后一步,我们要加入偏残差本身。偏残差是平滑项的估计值+整个模型的残差。
#添加偏残差。 points(temp,partial.resids)
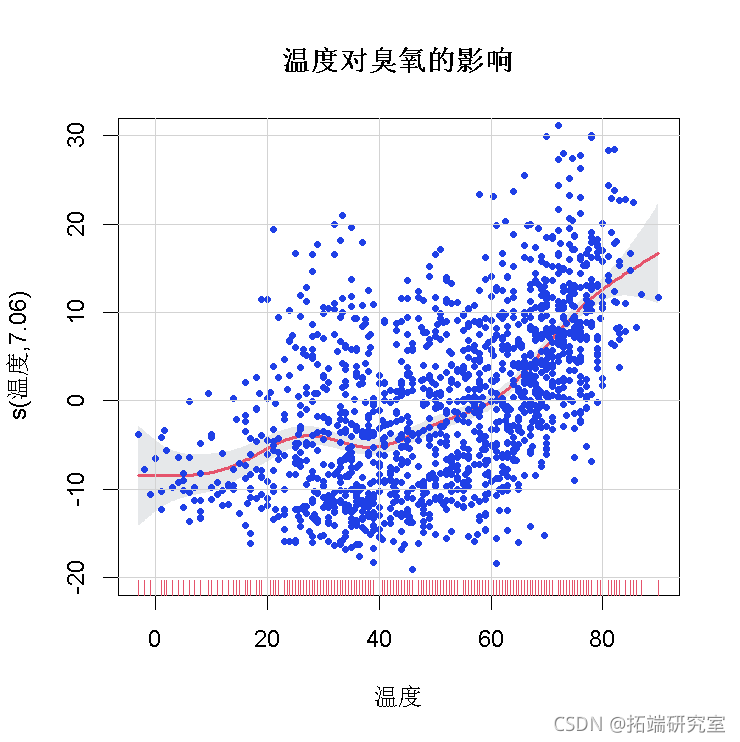
为便于参考,这里是完整模型的摘要。
模型 – 温度对臭氧的影响

可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

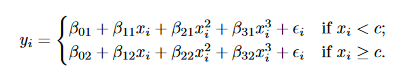
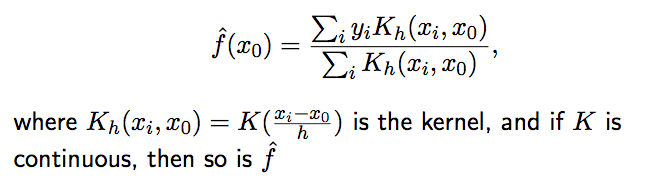

 R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据
R语言广义加性模型GAM、Tweedie分布的SaaS客户生命周期价值CLV预测研究——非线性关系捕捉与异方差性适配创新|附代码数据 【视频】R语言广义加性模型GAMs非线性效应、比较分析草种耐寒性实验数据可视化
【视频】R语言广义加性模型GAMs非线性效应、比较分析草种耐寒性实验数据可视化 R语言拟合改进的稀疏广义加性模型(RGAM)预测、交叉验证、可视化
R语言拟合改进的稀疏广义加性模型(RGAM)预测、交叉验证、可视化 R语言惩罚逻辑回归、线性判别分析LDA、广义加性模型GAM、多元自适应回归样条MARS、KNN、二次判别分析QDA、决策树、随机森林、支持向量机SVM分类优质劣质葡萄酒十折交叉验证和ROC可视化
R语言惩罚逻辑回归、线性判别分析LDA、广义加性模型GAM、多元自适应回归样条MARS、KNN、二次判别分析QDA、决策树、随机森林、支持向量机SVM分类优质劣质葡萄酒十折交叉验证和ROC可视化



