
这篇文章中我们可以编写自己的代码来计算套索(lasso)回归
我们必须定义阈值函数
可下载资源
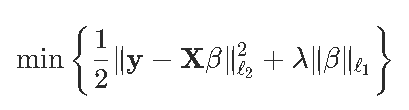
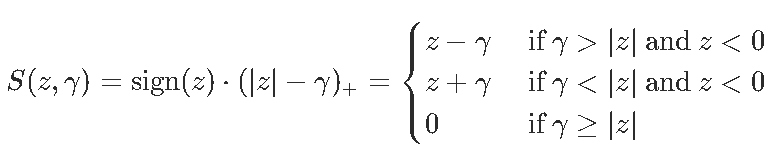
要解决我们的优化问题,设置
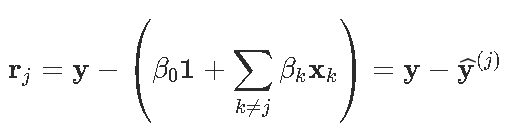
这样就可以等效地写出优化问题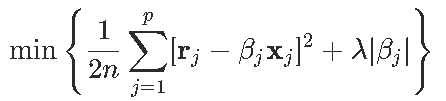
因此
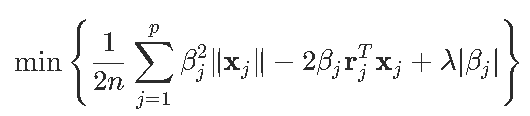
一个得到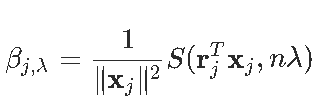
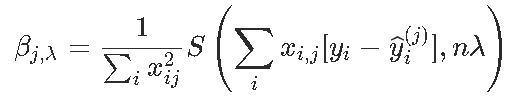
同样,如果有权重ω=(ωi),则按坐标更新将变为
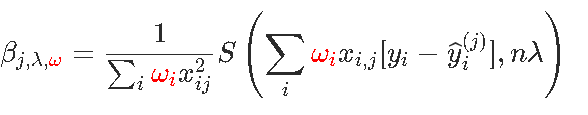
计算此分量下降的代码是
lasso = function(X,y,beta,lambda,tol=1e-6,maxiter=1000){
beta0 = sum(y-X%*%beta /(length(y))
beta0list[1] = beta0
for (j in 1:maxiter){
for (k in 1:length beta)){
r = y - X[,-k]%*%beta[-k] - beta0*rep(1,length(y )
beta[k] = (1/sum(omega*X[,k]^2) *
threshog(t(omega*r)%*%X[,k ,length(y *lambda)
}
beta0 = sum(y-X%*%beta)/(length(y))
obj[j] = (1/2)*(1/length(y))*norm(omega*(y - X%*%beta -
beta0*rep(1,length(y))),'F')^2 + lambda*sum(abs(beta))
if (norm(rbind(beta0list[j],betalist[[j]]) -
rbind(beta0,beta),'F') ) { break } 例如,考虑以下(简单)数据集,其中包含三个协变量
chicago = read.table("data.txt",header=TRUE,sep=";")
我们可以“标准化”
for(j in 1:3) X[,j] = (X[,j]-mean(X[,j]))/sd(X[,j])
y = (y-mean(y))/sd(y)要初始化算法,使用OLS估算
lm(y~0+.,)$coef
例如
lasso(X,y,beta_init,lambda=.001)
$obj
[1] 0.001014426 0.001008009 0.001009558 0.001011094 0.001011119 0.001011119
$beta
[,1]
X_1 0.0000000
X_2 0.3836087
X_3 -0.5026137
$intercept
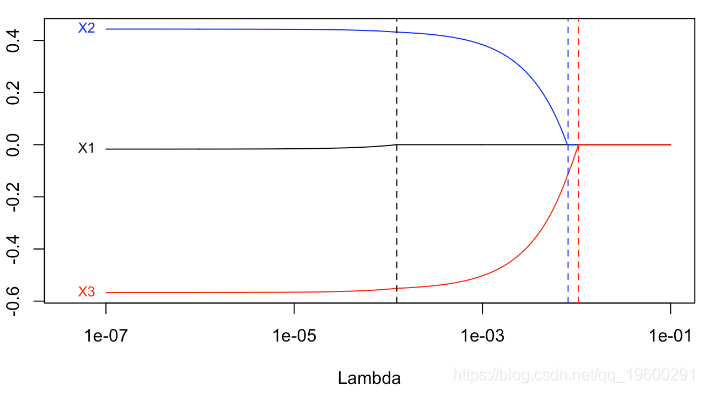
[1] 2.060999e-16我们可以通过循环获得标准的lasso图

 Python用Ridge、Lasso、KNN、SVM、决策树、随机森林、XGBoost共享单车数据集需求预测及动态资源调配策略优化|附代码数据
Python用Ridge、Lasso、KNN、SVM、决策树、随机森林、XGBoost共享单车数据集需求预测及动态资源调配策略优化|附代码数据 Python、R语言分析在线书籍销售数据:梯度提升树GBT、岭回归、Lasso回归、支持向量机SVM实现多维度特征的出版行业精准决策优化与销量预测|附代码数据
Python、R语言分析在线书籍销售数据:梯度提升树GBT、岭回归、Lasso回归、支持向量机SVM实现多维度特征的出版行业精准决策优化与销量预测|附代码数据 R与Python用去偏LASSO模型、OW重叠加权、HDMA高维中介分析、SIS迭代筛选挖掘甲基化数据在童年虐待与PTSD关联中的介导机制与预测研究|附代码数据
R与Python用去偏LASSO模型、OW重叠加权、HDMA高维中介分析、SIS迭代筛选挖掘甲基化数据在童年虐待与PTSD关联中的介导机制与预测研究|附代码数据 Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据
Python梯度提升树、XGBoost、LASSO回归、决策树、SVM、随机森林预测中国A股上市公司数据研发操纵融合CEO特质与公司特征及SHAP可解释性研究|附代码数据



