因子实验在农业中非常普遍，它们通常用于测试实验因素之间相互作用的重要性。
例如，可以在两种不同的施氮水平（例如高和低）下进行基因型评估，以了解基因型的排名是否取决于养分的可用性。
对于那些不太了解农业的人，我只会说这样的评估是相关的，因为我们需要知道我们是否可以推荐相同的基因型，例如，在传统农业（高氮可用性）和有机农业中农业氮的可用性。
可下载资源
测试非线性回归中的交互作用
让我们考虑一个实验，在该实验中，我们在完整的区组因子设计中以两种氮含量（“高”和“低”）测试了三种基因型（为了简便起见，我们称它们为 A、B 和 C），并进行四次重复。在八个不同的时间（播种后天数：DAS）从 24 个地块中的每一个中取出生物量子样本，以评估生物量随时间的增长。
假如你想做开个蛋糕店，要提供一个最佳口感蛋糕的食谱，要能试用于不同的店面，不同的厨师（有经验的，没经验的）：
那么设计一个DOE的意义就在与研究每一种可能的影响因素和结果之间的相关性，而它实际能够提供的帮助包括：
-
研究原料之间的可替代性，在蛋糕的例子里，很显然面粉，糖和鸡蛋都可以来自于不同的品质/品牌，这种品质/品牌之间的差别，会对最后蛋糕的成品影响有多大。
-
找出最具影响的因子，显然，烤箱的温度高与低，糖量多与少， 面粉多与少，鸡蛋多与少，都会直接决定最后蛋糕的口感，那么究竟哪一个因素是影响最大的？也就是在制作过程中要求最为严格的？
-
找出最优解，在找出最具影响的因子之后，就要决定这个因子在什么样的设定下才能给出最有结果，很显然在实际生产应用中，往往是多个因子共同作用，最优解的意义就在于寻求出这些因子之间的平衡
-
减少recipe的限制，增加整个蛋糕制作过程的可重复性，也就是减少影响因子，DOE有助于分析出哪些因子是对最后结果并无影响的，或者影响甚微的，那这些影响因子在最后的recipe里就有很大自由度，明白那些因子影响甚微的意义还在于，在生产过程中即时看到这些变化，也能从一定程度上保证品质不受影响，比如说面粉的品牌并不影响蛋糕口感，那么在制作过程中面粉的品牌就不会是主要控制对象，研究这个意义在于你的recipe可重复性越高，不同人做出来的蛋糕（或者产品）浮动越小，这点在mass production尤其重要。
-
平衡得失，举个例子说，你希望蛋糕又要好看又要好吃，可是实验结果告诉你，要好看的话烘烤时间不能太久，可是同时，烘烤时间久一点蛋糕好吃一点，这时候就要回过头去看你的DOE里，怎么能找出这个让蛋糕既好看又好吃的烘培时间
加载数据并将“Block”变量转换为一个因子。
head(dataset)
数据集由以下变量组成：
- ‘Id’：观察的数字代码
- ‘DAS’：即播种后的天数。这是采集样本的时刻
- ‘Block’, ‘Plot’, ‘GEN’ 和 ‘N’ 分别代表每个观察的块、图、基因型和氮水平
- “产量”代表收获的生物量。
查看观察到的增长数据，如下图所示。
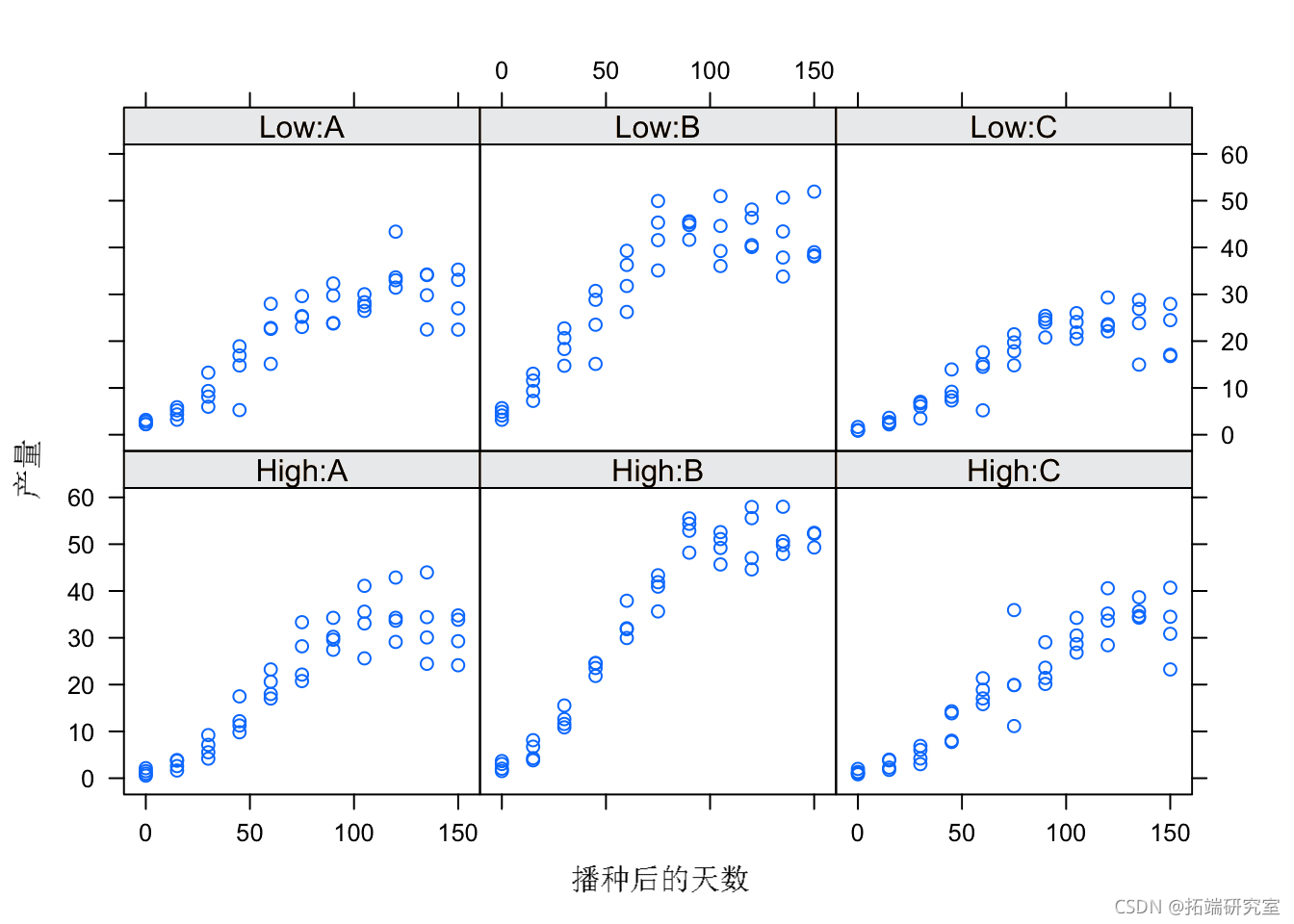
我们看到增长是对称的（大概是逻辑的）并且观察的方差随着时间的推移而增加，即方差与期望因变量成正比。
问题是：我们如何分析这些数据？
模型
我们可以凭经验假设生物量和时间之间的关系是逻辑的：
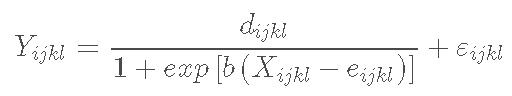
其中Y是第i个基因型、第j个氮水平、第k个区块和第l个小区在X时间观察到的生物量产量，d是时间进入无穷大时的最大渐进生物量水平，b是拐点处的斜率，而e是生物量产量等于d/2时的时间。我们主要对参数d和e感兴趣：第一个参数描述基因型的产量潜力，而第二个参数给出生长速度的测量。
每个小区都有重复测量，因此，模型参数可能显示出一些变化，取决于基因型、氮水平、区块和小区。特别是，假设b是相当恒定的，并且独立于上述因素，而d和e可能根据以下公式发生变化，这是可以接受的。
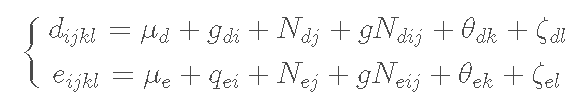
其中，对于每个参数，μμ是截距，gg是第i个基因型的固定效应，NN是第j个氮水平的固定效应，gNgN是固定交互效应，θ是区块的随机效应，而ζζ是区块内地块的随机效应。这两个方程完全等同于通常用于线性混合模型的方程，在双因素因子区块设计的情况下，其中ζζ是残差误差项。事实上，原则上，我们也可以考虑两步法的拟合程序，即我们。
- 将逻辑模型拟合到每个图的数据并获得 d 和 e 的估计值
- 使用这些估计来拟合线性混合模型
我们不会在这里追求这种两步法，我们将专注于一步拟合。
错误的方法
如果观察是独立的（即没有块和没有重复测量），这个模型可以通过使用传统的非线性回归来拟合。
编码报告如下。产量 “是(∼)DAS的函数，通过一个三参数的Logistic函数。对于基因型和氮水平的不同组合必须拟合不同的曲线（id = N:GEN），尽管这些曲线应该部分地基于共同的参数值（’models = …）。model”参数需要一些补充说明。它必须是一个矢量，其元素数与模型中的参数数一样多（在本例中是三个：B、D和E）。每个元素代表一个变量的线性函数，并按字母顺序指向参数，即第一个元素指b，第二个指d，第三个指e。参数b不依赖于任何变量（’~1’），因此在不同的曲线上拟合出一个常数；d和e依赖于基因型和氮水平的完全因子组合（~N*GEN = ~N + GEN + N:GEN）。最后，我们使用参数’bcVal = 0.5’来指定我们打算使用转换两边方法，即对方程的两边进行对数转换。这对于考虑异方差是必要的，但它不影响参数估计。
rm(Yield ~ DAS, dta =daas, id = GEN：N, model = c( ~ 1, ~ N\*GEN, ~ N\*GEN))
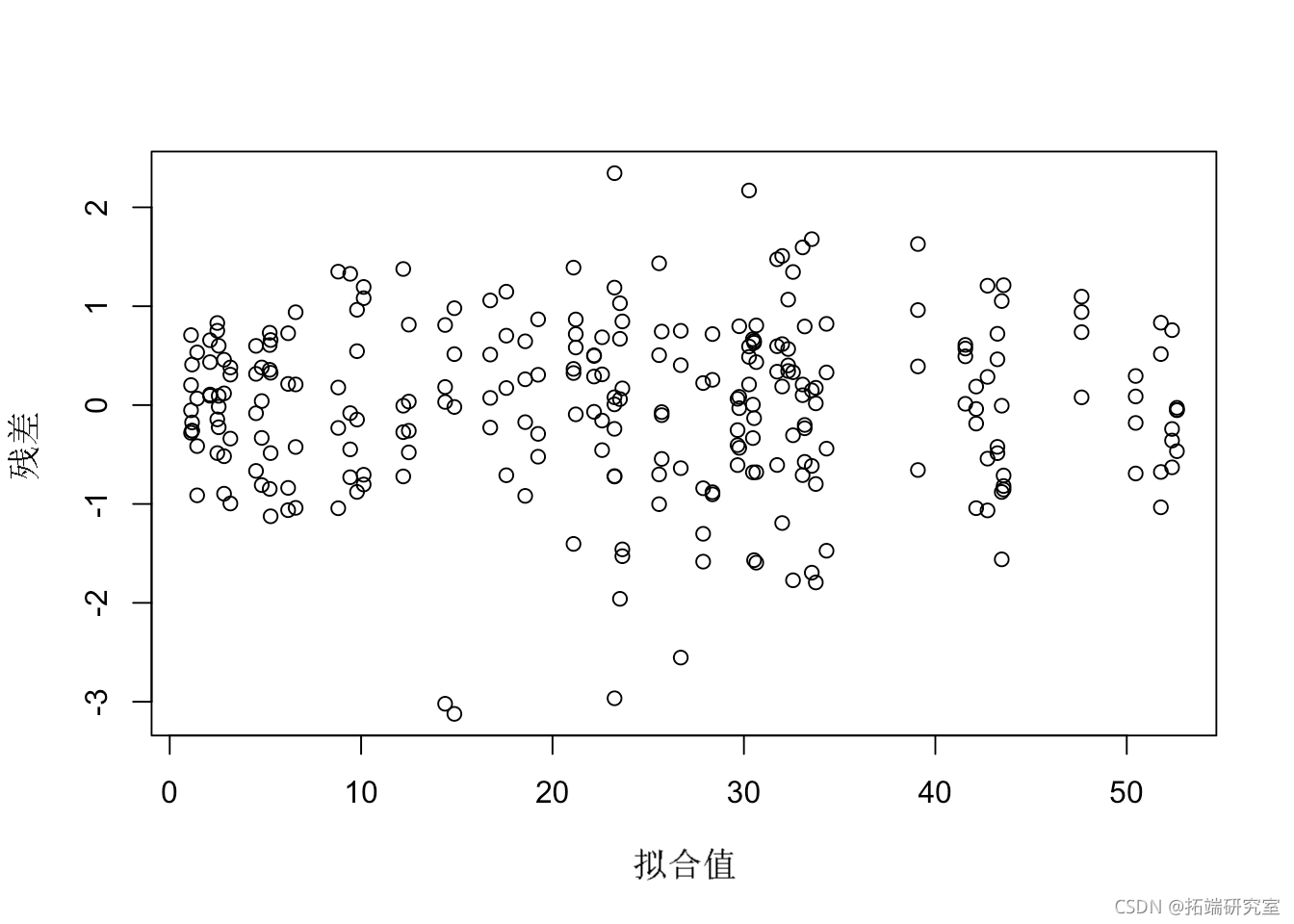
这个模型对于其他情况（无区块和无重复测量）可能是有用的，但在我们的例子中是错误的。事实上，观测值在区块和地块内是聚在一起的；如果忽略这一点，我们就违反了模型残差独立的假设。残差与拟合值的图显示，不存在异方差的问题。
随时关注您喜欢的主题
考虑到上述情况，我们必须在这里使用不同的模型，尽管我将证明这种拟合可能会很有用。
非线性混合模型拟合
为了解释观察的类，我们切换到非线性混合效应模型（NLME）。一个不错的选择是’nlme()’ 函数（Pinheiro 和 Bates，2000），尽管有时语法可能很麻烦。我们需要指定以下内容：
- 模型参数的线性函数。nlme’函数中的’fixed’参数与上面函数中的’models’参数非常相似，即它需要一个列表，其中每个元素都是变量的线性函数。唯一的区别是，参数名称需要在函数的左侧指定。
- 模型参数的随机效应。这些是通过使用 “随机 “参数来指定的。在这种情况下，参数d和e有望在一个区块内的不同区块和不同地块之间显示随机变化。为了简单起见，由于参数b不受基因型和氮水平的影响，我们也希望它在区块和地块之间不显示任何随机变化。
- 模型参数的起始值。我们需要指定模型参数的初始值。在这种情况下，我决定使用上面非线性回归的输出。
方程两边的变换。
nlme(sqtYld ~ srtLS.L3(DAS, b, d, e) tTable
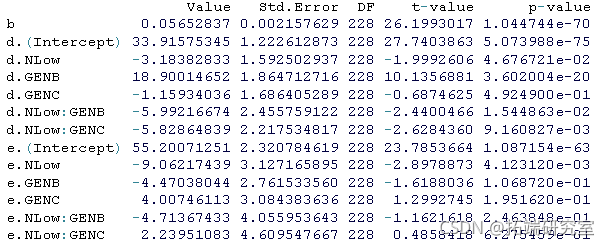
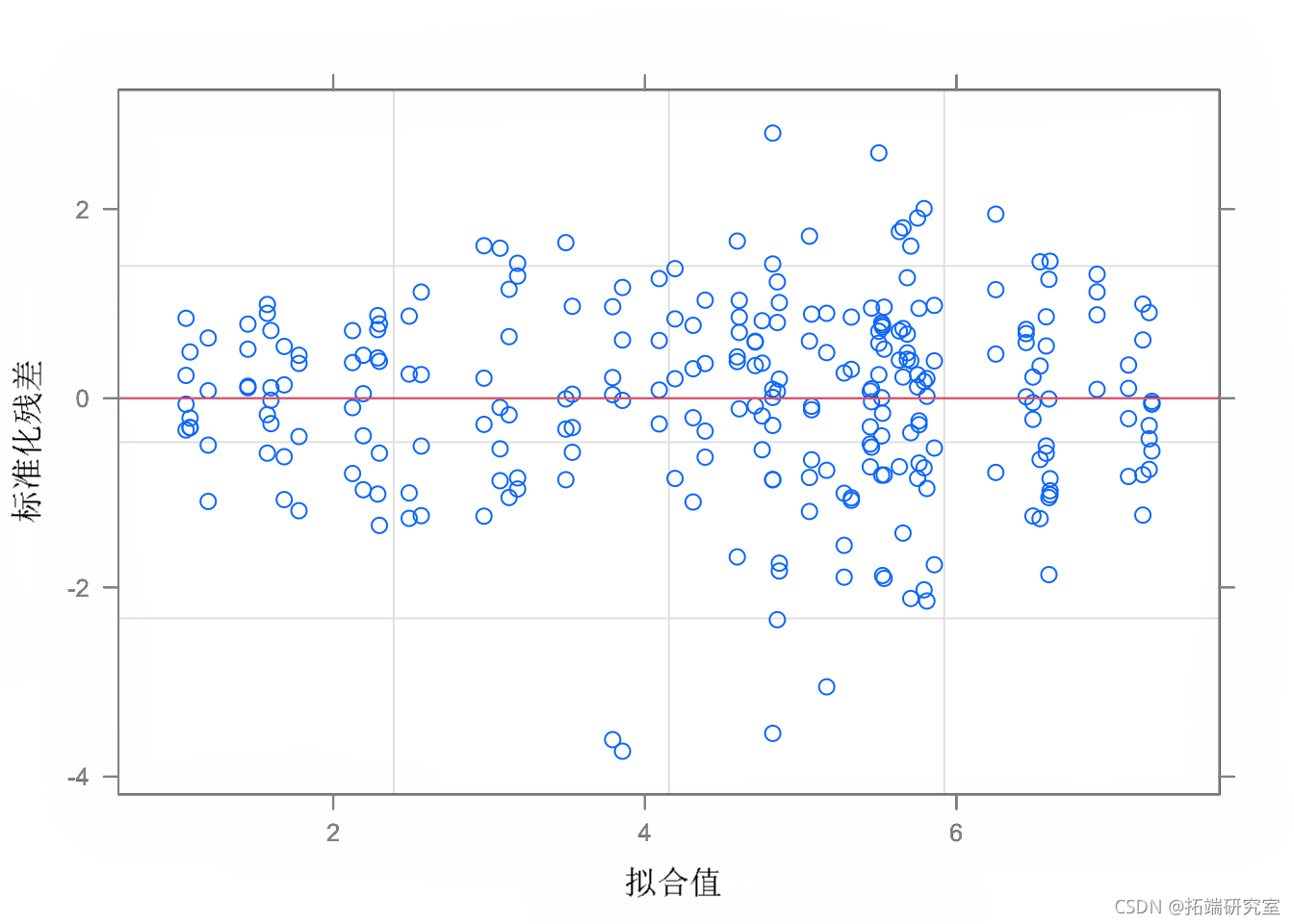
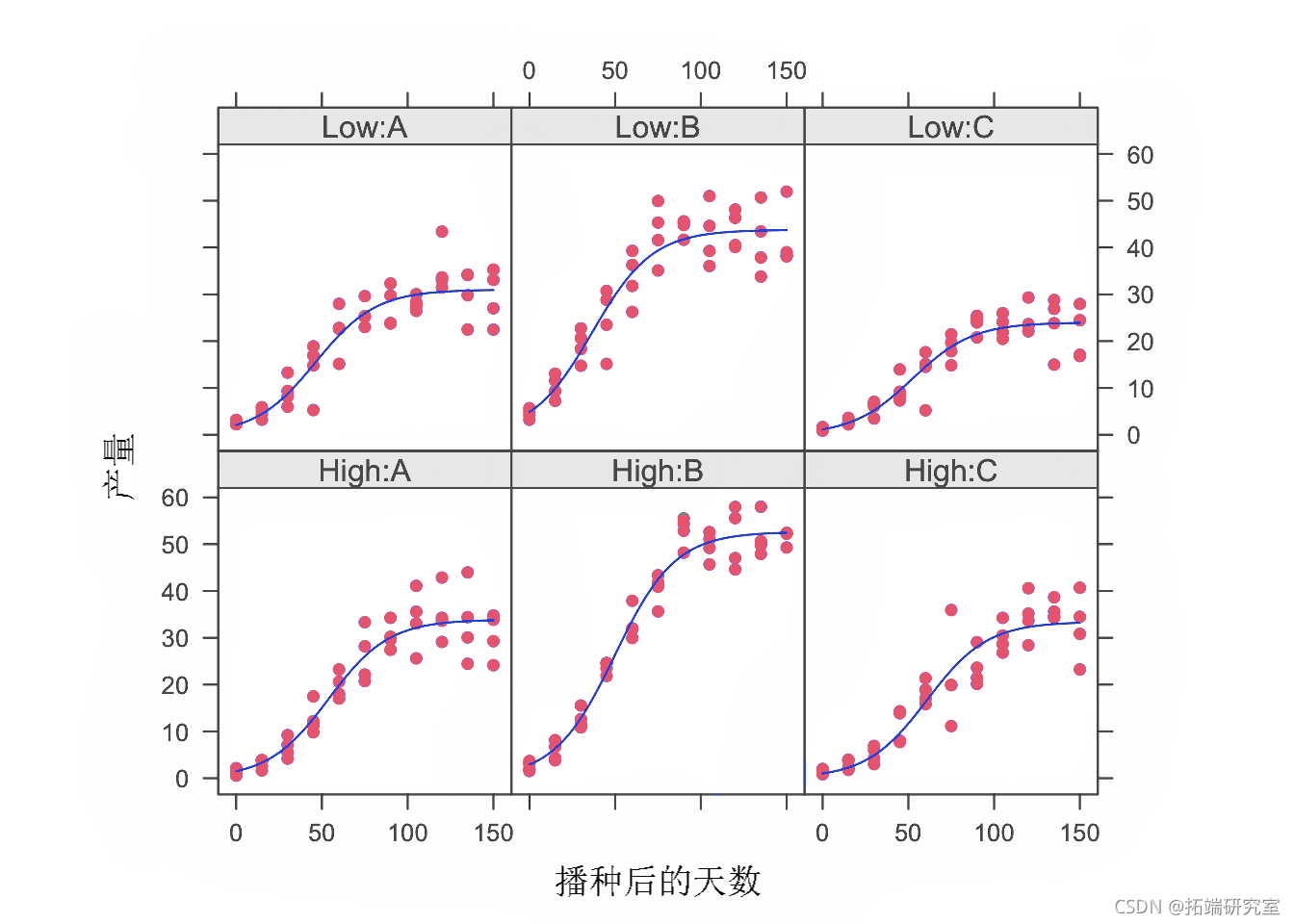
从上图中，我们看到整体拟合良好。随机效应的固定效应和方差分量按如下方式获得：
summary(mdnle1)
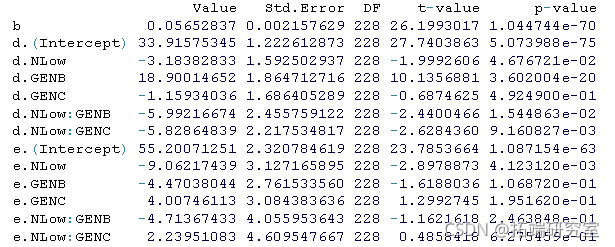
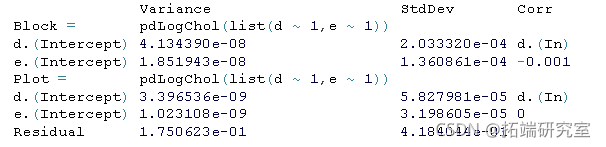
现在，让我们回到我们最初的目的：测试 “基因型x氮 “交互作用的显著性。事实上，我们有两个可用的测试：一个是参数d，一个是参数e。首先，我们对两个 “简化 “模型进行编码。为此，我们把固定效应从’~ N*GEN’改为’~ N + GEN’。同样在这种情况下，我们使用非线性回归拟合来获得模型参数的起始值，用于下面的NLME模型拟合。
我们可以通过使用似然比检验来比较这个模型和完整的模型 “modnlme1″。
mdNave2 <- Yied ~ DAS modes = c( ~ 1, ~ N + GEN, ~ N * GEN mdnle2 <-sqrt(Yeld) ~ sqrt(NS.3(DAS, b, d, e mdaie3 <- Yied ~ DAS crid = N:GEN modls = c( ~ 1, ~ N*GEN, ~ N + GEN mdne3 <- sqrt(Yild) ~ sqrt(NS.L3(DAS, b, d, e ranom = d + e~ 1|Blck/Pot fixd = lit(b ~ 1 d ~ N*GN, e ~ N + GN)
让我们考虑第一个缩小的模型’modnlme2’。在这个模型中，”基因型x氮 “的交互作用已经被移除，用于d参数。
aova(mode1, mdne2)
该检验是显著的，但两个模型的AIC值非常接近。考虑到混合模型中的LRT通常比较宽松，应该可以得出结论，”基因型x氮素 “的交互作用不显著，因此，用d参数衡量的基因型在产量潜力方面的排名应该与氮素水平有关。
现在让我们考虑第二个简化模型“modnlme3”。在第二个模型中，“e”参数的“基因型 x 氮”交互作用已被删除。我们还可以使用似然比检验将此简化模型与完整模型“modnlme1”进行比较：
anva(mole1, mdle3)
在这第二次检验中，”基因型x氮素 “交互作用的不显著性似乎比第一次检验更可信。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
R语言混合模型回归GBTM群组轨迹模型绘图可视化研究
R语言贝叶斯分析：INLA 、MCMC混合模型、生存分析肿瘤临床试验、间歇泉喷发时间数据应用|附数据代码
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
Python用线性回归和TensorFlow非线性概率神经网络不同激活函数分析可视化
