在我们的数理统计课程中,已经看到了大数定律(这在概率课程中已经被证明),证明
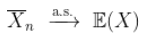
给出一组i.i.d.随机变量 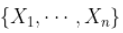 ,其中有
,其中有
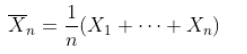
可下载资源
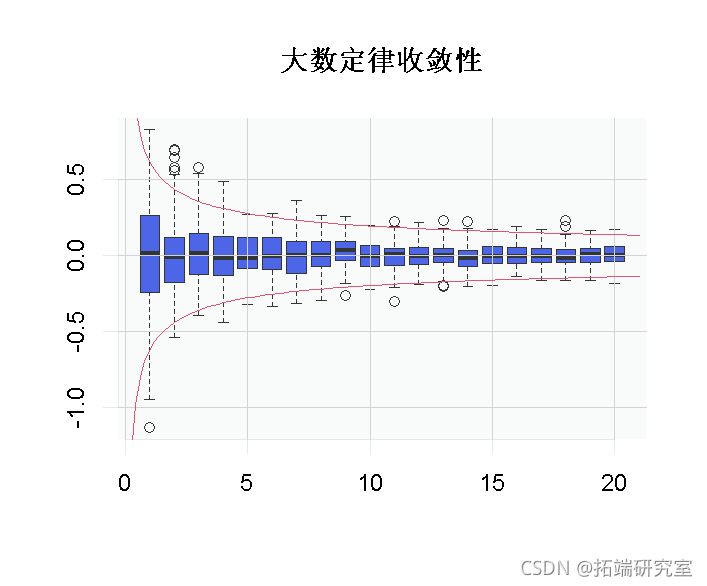
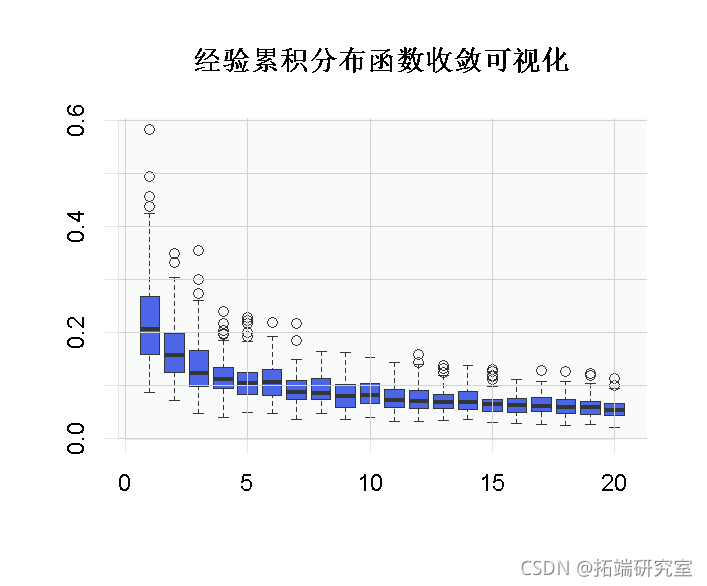
为了直观地看到这种收敛性,我们可以使用
> for(i in 1:20)B\[,i\]=mean_samples(i*10) > boxplot(B)
先介绍一下大数定理。网上查了一下由下面几个版本。
切比雪夫大数定律:用统计方法来估计期望的理论依据。
直观含义很简单,就是,求平均。举个例子来说,加入班上由 80个同学,那么随机选一个同学,他的身高应该是班里面的平均值。
贝努利大数定律:事件 发生的频率 依概率收敛于事件 的概率 。明确了频率的稳定性,当 很大时,事件发生的频率与概率有较大偏差的可能性很小。
这个版本定义是从概率的角度,当N很大的时候,事件A发生的概率等于A发生的频率。
中心极限定理
自然界与生产中,一些现象受到许多相互独立的随机因素的影响,如果每个因素所产生的影响都很微小时,总的影响可以看作是服从正态分布的.
在独立同分布的情况下,无论 的分布函数为何,它们的平均数 当 充分大的时候总是近似地服从正态分布。
所以这样就很好理解为什么身高/智商/考试成绩符合正态分布了. 因为这些属性都取决于非常非常多的变量, 相当于一个有着n多股票的投资组合.这样他们总体组成的表现就会像他们的平均分布正态分布。
所以两个定理的核心思想都是平均。不管单个的样本(大数定理),还是分布(中心极限定理)。如果N足够大都会趋向于平均。
也可以直观地看到边界
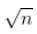
(用于中心极限定理,获得极限的非退化分布)。
我们一直在讨论经验累积分布函数的特点。
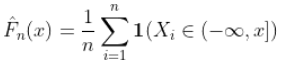
我们已经看到了格利文科-坎特利定理,该定理指出
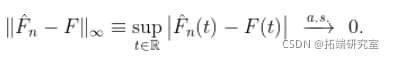
为了直观地看到这种收敛。这里我使用了一个技巧可视化
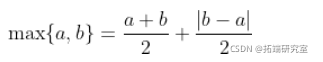
获得两个矩阵之间的最大值(分量)。
+ Df=(D1+D2)/2+abs(D2-D1)/2 > boxplot(B)
我们还讨论了经验累积分布函数的逐点渐近正态性
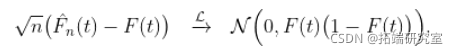
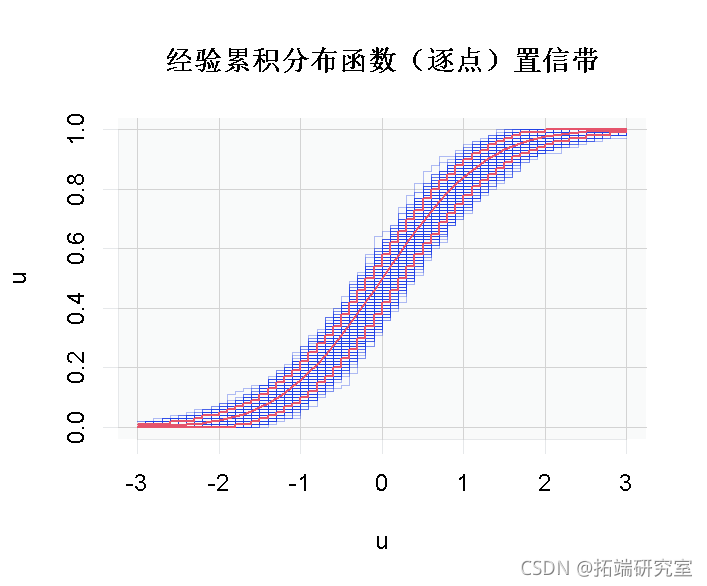
在这里,又可以把它形象化。第一步是计算经验累积分布函数的几条轨迹
> plot(u,u)
请注意,我们可以计算(逐点)置信带
> lines(u,apply(M,1,function(x) quantile(x,.05) > lines(u,apply(M,1,function(x) quantile(x,.95)
现在,如果我们专注于一个特定的点,我们可以直观地看到渐近正态性(即当我们有一个大小为100的样本时,几乎是正态的)。
随时关注您喜欢的主题
> hist(y) > lines(vu,dnorm(vu,pnorm(x0) + sqrt((pnorm(x0)*(1-pnorm(x0)))/100)
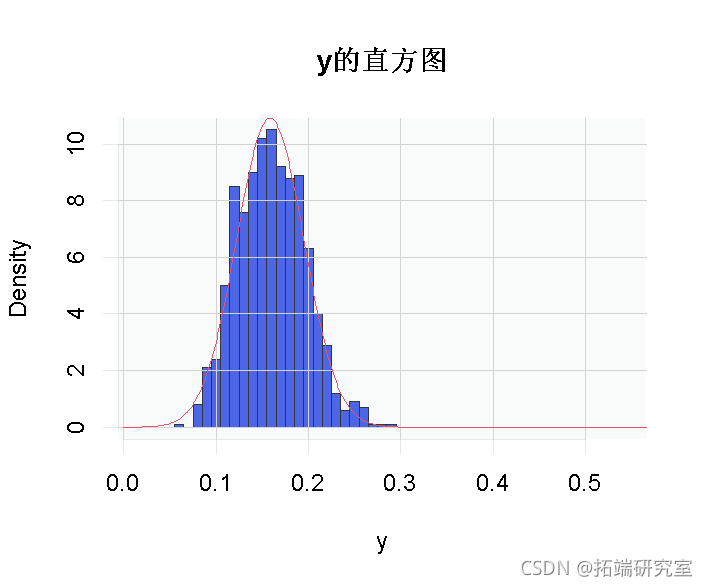
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!



 2026年智旅新纪元AI旅游产业融合全景报告:智慧化、个性化、可持续|附240+份报告PDF、数据、可视化模板汇总下载
2026年智旅新纪元AI旅游产业融合全景报告:智慧化、个性化、可持续|附240+份报告PDF、数据、可视化模板汇总下载 2025年AI智能体时代重塑企业未来报告:政务金融落地、技术架构与商业化|附180+份报告PDF、数据、可视化模板汇总下载
2025年AI智能体时代重塑企业未来报告:政务金融落地、技术架构与商业化|附180+份报告PDF、数据、可视化模板汇总下载 Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化
Python酒店预订数据:随机森林与逻辑回归模型ROC曲线可视化 R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素
R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素



