本文与以下两个问题有关。你应该如何在回归中添加虚拟变量？你应该如何解释结果？
如果使用一个例子，我们可能会更容易理解这些问题。
假设我们想研究工资是如何由教育、经验和某人是否担任管理职务决定的。
可下载资源
数据
假设：
- 每个人都从年薪4万开始。
- 实践出真知。每增加一年的经验，工资就增加5千。
- 你学得越多，你的收入就越多。高中、大学和博士的年薪增长分别为0、10k和20k。
- 海面平静时，任何人都可以掌舵。对于担任管理职位的人，要多付20k。
- 天生就是伟大的领导者。对于那些只上过高中却担任管理职位的人，多给他们3万。
- 随机因素会影响工资，平均值为0，标准差为5千。
通常，分析师在回归分析中需要使用定性变量作为自变量。有一种类型的定性变量，称为虚拟变量，如果特定条件为真，则取值为1；如果条件为假，则取值为0。例如，假设我们要检验一月份的股票收益是否与剩余月份不同。我们在回归中纳入一个自变量X1t，该变量对应每年一月份的取值为1，对于一年中的其他月份的取值为0。我们估计回归模型
Yt= b0 + b1X1t +εt
在该等式中，系数b0是除1月份以外的月份中的Yt的平均值，b1是1月份的Yt的平均值与1月份以外的月份中的Yt的平均值的差。
我们需要谨慎选择回归中虚拟变量的数量。规则是，如果要区分n个类别，则需要n-1个虚拟变量。例如，为了区分一月和一月以外的月份（n= 2个类别），我们使用一个虚拟变量（n-1= 2-1 =1）。如果要区分一年中的每个季度，我们将使用三个虚拟变量。如果我们错误地选择了四个虚拟变量，这样就违反了多元回归模型的假设2，因此无法对回归进行估计。以下案例说明了在使用每月数据进行回归时使用虚拟变量的情况。
下面是部分数据和摘要。
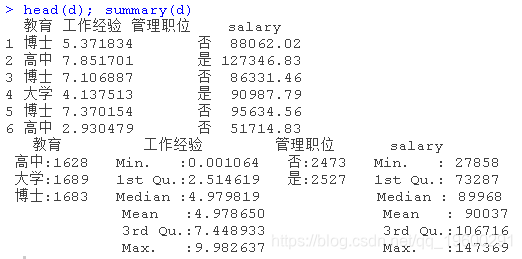
绘制数据
有和没有管理职位的人的工资和教育之间的关系。
jitter(alpha=0.25,color=colpla\[4\])+
facet_wrap(~管理职位)+
boxplot(color=colpla\[2\])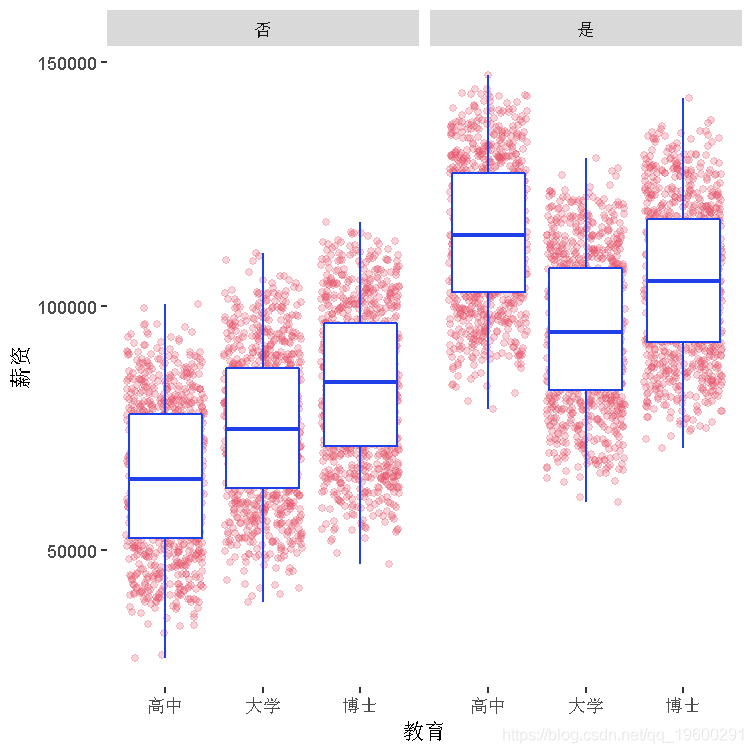
有管理职位和没有管理职位的人的工资和经验之间的关系，以教育为基础。
stat_smooth(method = "lm")+
facet_wrap(~管理职位)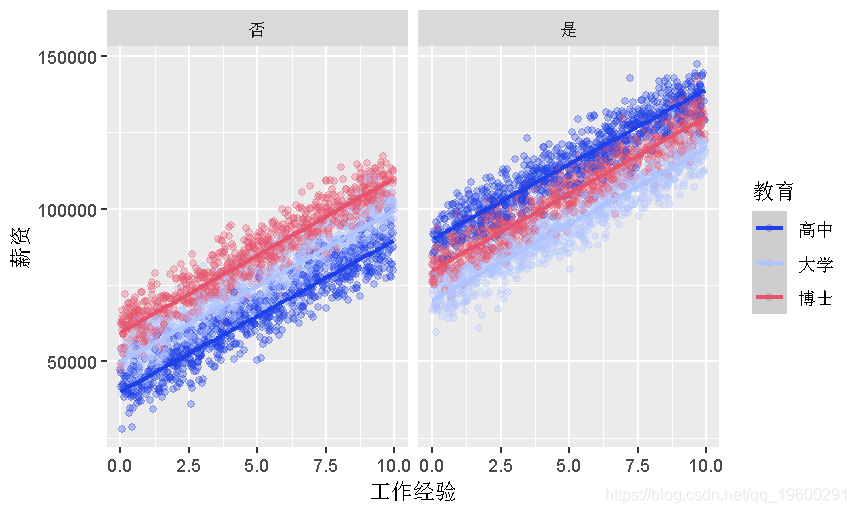
回归分析
忽略教育和管理之间的相互作用
我们只将工资与教育、经验和管理职位进行回归。其结果是
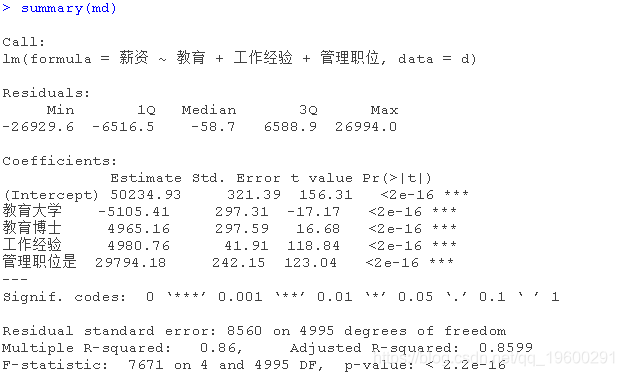
虽然这些参数在统计学上是有意义的，但这并没有任何意义。与高中相比，大学学历怎么可能使你的工资减少5105？
正确的模型应该包括教育和管理职位的交互项。
添加教育和管理之间的交互作用
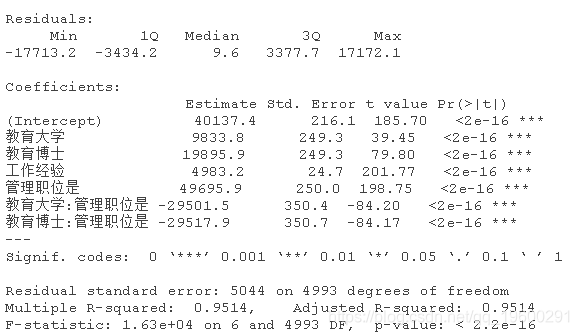
现在，让我们添加教育和管理之间的交互项，看看会发生什么。
随时关注您喜欢的主题
对结果的解释
现在的结果是有意义的。
- 截距为40137（接近4万）是基本保障收入。
- 教育的基数是高中。与高中相比，大学教育可以平均增加9833元（接近1万）的工资。与高中相比，博士教育可以增加19895元（接近2万）的工资。
- 多一年的工作经验可以使工资增加4983元（接近5千）。
- 担任管理职位的高中毕业生有49695元的溢价（接近5万）。这些人是天生的领导者。
- 与担任管理职位的高中毕业生相比，担任管理职位的大学毕业生的溢价减少了29965.51至29571（49735.74-29965.51，接近2万）。
- 与高中毕业生担任管理职位相比，博士毕业生担任管理职位的溢价减少了29501至19952.87（接近2万）。另外，你可以说管理职位产生了20K的基本溢价，而不考虑教育水平。除了这2万外，高中毕业生还能得到3万，使总溢价增加到5万。
检验是否违反了模型的假设
为了使我们的模型有效，我们需要满足一些假设。
- 误差应该遵循正态分布
正态Q-Q图看起来是线性的。所以这个假设得到了满足。
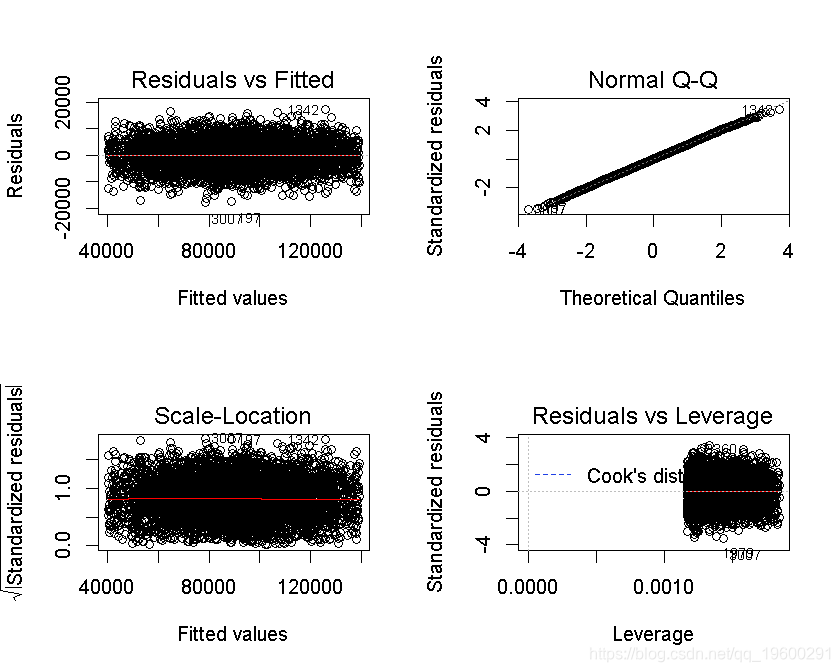
- 没有自相关
D-W检验值为1.8878，接近2，因此，这个假设也满足。
- 没有多重共线性
预测变量edu、exp和mngt的VIF值均小于5，因此满足这一假设。
如果只用高中生的数据，你会得到这样的结果。
用数据的子集进行回归
你可以通过用一个数据子集运行模型来获得同样的结果。你可以将数据按教育程度分成子集，并在每个子集上运行回归模型，而不是使用一个教育的虚拟变量。
sub<-d %>%
+ filter(教育=="高中")
仅凭大学生的数据，你就能得到这个结果。
只用来自博士生的数据，你会得到这个结果。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频】N-Gram、逻辑回归反欺诈模型文本分析招聘网站欺诈可视化|附数据代码
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
R语言拟合线性混合效应模型、固定效应、随机效应参数估计可视化生物生长、发育、繁殖影响因素
