在本文中，我将向您展示如何模拟股票价格的Heston随机波动率模型。它是一种期权估值方法，它考虑到同一资产在给定时间交易的不同期权的波动性变化。
Heston模型试图通过使用随机过程来模拟波动率和利率来重新创建市场定价。
可下载资源
Heston模型的特点是将波动率函数的平方根包含在整个定价函数中。
风险中性的条件下的期权定价的基本公式： ，
其中 是一个股价的随机过程，
为股价在到期日
的价格，
是期权的 Payoff 函数，
为无风险利率；
将上边的公式写成积分形式： ，
其中 是股价
的概率密度函数(probability density function PDF)。对于简单的期权不难得到
的 analytical expression；对于一些复杂的期权，只能通过蒙特卡洛模拟(MC)来得到一个近似解(Approximation)，就比如今天的障碍期权。
MC的基本思路是在到期日 时模拟多个离散的
，这个模拟出来的 empirical PDF 是一个Dirac delta functions
，这个模拟的 PDF 可以写成：
。
理论上来说，随着模拟次数的增加，这个模拟的 PDF 会收敛于真实 PDF：
，
因此，可以把最初的公式写成：
对于固定的无风险利率，描述为：
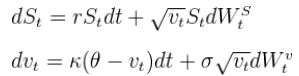
通过使用这种模型，可以得出欧洲看涨期权的价格 。
这是函数的描述。
callHestoncf(S, X, tau, r, v0, vT, rho, k, sigma){
# S = 股价在到期日的价格, X = 行权价格, tau = 到期日
# r = 为无风险利率, q = 股息收益
# v0 = 初始方差, vT = 长期方差
# rho = 相关系数, k = 是Vt回归至θ的速度；
# sigma = 波动率
}
现在，进行蒙特卡洛定价。我们将为3个欧洲看涨期权定价，具有3种不同的行权价格。我们在15年中使用100000个模拟，每个月进行一次。以下是仿真的参数：
#初始价格
S0 <- 100
# 模拟次数（可以随意减少）
n <- 100000
# 抽样频率
freq <- "monthly"
# 波动率均值回复速度
kappa <- 0.003
#波动率
volvol <- 0.009
# 相关性。成交量和现货价格
rho <- -0.5
# 初始方差
V0 <- 0.04
# 长期的方差
theta <- 0.04
#初始短期利率
r0 <- 0.015
# 期权到期日
horizon <- 15
#期权行权价格
strikes <- c(140, 100, 60)为了使用模拟Heston模型，我们首先需要定义如何进行模拟。
此函数提供一个包含2个成分的列表，每个成分包含模拟的随机高斯增量。
# 随机波动模拟
sim.vol <- simdiff(n = n, horizon = horizon,
frequency = freq, model = "CIR", x0 = V0,
theta1 = kappa*theta, theta2 = kappa,
theta3 = volvol, eps = shocks[[1]])
# 股票价格模拟
sim.price <- simdiff(n = n, horizon = horizon,
frequency = freq, model = "GBM", x0 = S0,
theta1 = r0, theta2 = sqrt(sim.vol),
eps = shocks[[2]])现在，我们可以计算3种不同的期权价格。
# 到期股票价格（15年）
print(results)
strikes mcprices lower95 upper95 pricesAnalytic
1 140 25.59181 25.18569 25.99793 25.96174
2 100 37.78455 37.32418 38.24493 38.17851
3 60 56.53187 56.02380 57.03995 56.91809
从这些结果中，我们看到这三个期权的蒙特卡洛价格与使用函数（直接使用公式来计算价格）计算出的价格相当接近。95％的置信区间包含理论价格。
随时关注您喜欢的主题
下面是期权价格，作为模拟次数的函数。计算出的理论价格用蓝色绘制，蒙特卡洛平均价格用红色绘制，阴影区域表示均值（蒙特卡洛价格）周围的95％置信区间。
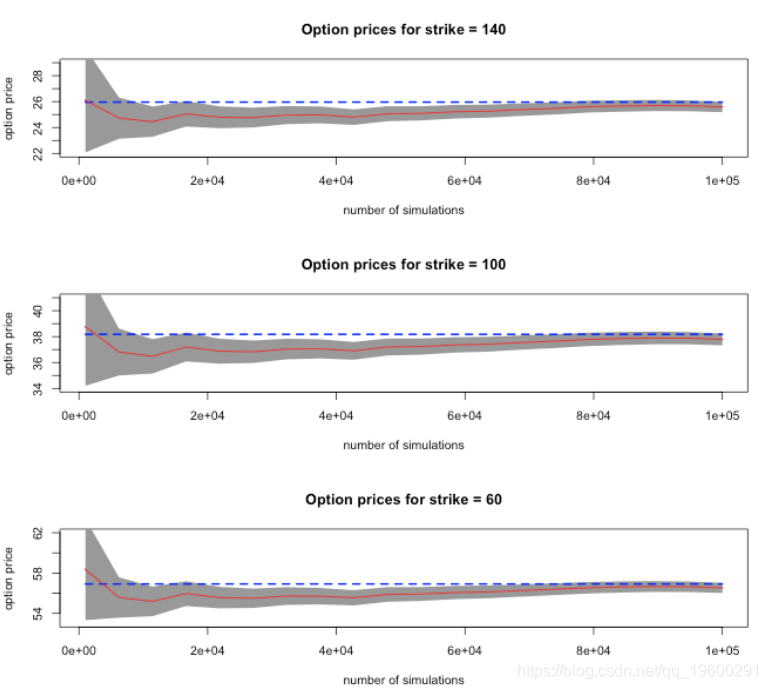
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言宏观经济学：IS-LM曲线可视化货币市场均衡
R语言代做编程辅导和解答GLM Coursework
