近年来，期权交易变得非常流行。在这篇文章中，您将学习一种期权交易策略，可以用来以较低的价格购买自己喜欢的股票。期权是一种衍生工具。

由Kaizong Ye，Coin Ge撰写

衍生物被誉为20世纪后期的金融革命。衍生产品类型为远期，期货，掉期和期权。衍生工具是从另一项基础资产中获取价值的工具。对于股票期权，其价格取决于标的股票。

可下载资源

完整程序、数据和文档（word）

衍生物被誉为20世纪后期的金融革命。衍生产品类型为远期，期货，掉期和期权。衍生工具是从另一项基础资产中获取价值的工具。对于股票期权，其价格取决于标的股票。

原始BSM

原始的BSM形式包含五个独立变量。我认为只要理解其中两到三个主要变量就够了，剩下只是技术性处理。

$C = SN(d_1)-N(d_2)Ke^{-rt}\label{eq:Black-Scholes}$

其中

$d_1 = \frac{ln(u/s) + (r+\sigma^2/2)t}{\sigma\sqrt{t}}$

$d_2 = d_1-\sigma\sqrt{t}$

从数学上看BSM实在太不美观了，这样复杂的公式严重影响所谓的物理直观。虽然公式的得来有历史研究的源流，但我们在这里稍微整理一下公式可以更方便理解。下面将把BSM化简成三变量函数。

对数化处理

第一个动手的地方是 $ln(u/s)$ ，对数学敏感的同学，面对分式的对数，可以马上想到

$ln(u/s)=ln(u)-ln(s)$

这里关系到价格服从对数正态分布的假设，所以标的价对行权价的差写为对数形式。

既然是对数正态分布的假设，不妨将原生的价格全部对数处理，于是标的价成为 $e^u$ 而行权价成为 $e^s$ ，这样，BSM公式中的对数项成为：

$ln(e^u/e^s)=u-s$

BSM公式成为：

$C = e^uN(d_1)-N(d_2)e^se^{-rt}$

其中

$d_1 = \frac{(u-s) + (r+\sigma^2/2)t}{\sigma\sqrt{t}}$

$d_2 = d_1-\sigma\sqrt{t}$

无风险收益率的简化

真实的期权交易中，特别是在低融资成本的时代，大部分情况可以忽略无风险收益率的影响。我们可以在理解BSM模型的主体之后，将无风险收益率作为调整因子加入进来再考虑。

注意无风险收益率 $r$ 出现的地方，均是和时间构成 $rt$ 或 $r\sqrt{t}$ 的形式。首先， $r$ 一定是很小的，特别是在宽松的市场环境中；其次，大部分真实期权交易都是中短期的，于是 $rt$ 或 $r\sqrt{t}$ 都近似于零。那么从数学上：

$\lim_{r \to 0}d_1= \frac{(u-s) + \sigma^2t/2}{\sigma\sqrt{t}}$

以及

$\lim_{r \to 0}C= e^uN(d_1)-e^sN(d_2)$

我们只考虑极限情况，那么BSM化简为：

$C = e^uN(d_1)-e^sN(d_2)$

其中

$d_1 = \frac{(u-s) + \sigma^2t/2}{\sigma\sqrt{t}}$

$d_2 = d_1-\sigma\sqrt{t}$

概率项的对称化

现在主公式已经有了优美的数学对称形式，而两个概率项看上去还不够美观。注意到我们可以把两项改写为对称的形式：

$d_1 = \frac{(u-s)}{\sigma\sqrt{t}} + \frac{\sigma\sqrt{t}}{2}$

$d_1 = \frac{(u-s)}{\sigma\sqrt{t}} - \frac{\sigma\sqrt{t}}{2}$

到目前为止，波动率和时间已经成为密不可分的整体，定义波-时为：

$\tau = \sigma\sqrt{t}$

我们可以把整个BSM集中在一个三变量函数中：

$C(u,s,\tau) = e^uN\Big(\frac{u-s}{\tau} + \frac{\tau}{2}\Big)-e^sN\Big(\frac{u-s}{\tau} - \frac{\tau}{2}\Big)$

于是我们完成了BSM的纯数学意义上的简化，它是行权价、标的价和波时的三变量函数，是不是比原始形式简化了很多？下面讨论物理直观。

时间极限

注意到，期权价格的独立变量之一是 $\tau = \sigma\sqrt{t} > 0$ 。波时作为整体影响到期权价格。这样解释了波动率和时间对期权价格的单调变化关系。是与距离到期日的时间之平方根 $\sqrt{t}$ 相关的，这直接解释了经典期权教科书中时间价值递减的非线性规律。时间价值随着时间递减，或者由于波动率下降而递减，本身可以反应为一个极限：

$\lim_{\tau \to 0} C = \lim_{\tau \to 0} e^uN\Big(\frac{u-s}{\tau} + \frac{\tau}{2}\Big)-e^sN\Big(\frac{u-s}{\tau} - \frac{\tau}{2}\Big) = e^u N(\pm\infty) - e^u N(\pm\infty)$

其中无穷的符号取决于价差 $u-s$ 。分情况讨论。

当 $u>s$ ，在 $\tau > 0$ 接近到期日时：

$\lim_{\tau \to 0} C = \lim_{\tau \to 0} e^uN\Big(\frac{u-s}{\tau} + \frac{\tau}{2}\Big)-e^sN\Big(\frac{u-s}{\tau} - \frac{\tau}{2}\Big) = e^u N(+\infty) - e^s N(+\infty)$

由正态分布公式：

$N(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x} e^{-z^2/2}dz$

有 $N(+\infty)=1$ ，于是

$\lim_{\tau \to 0} C = e^u N(+\infty) - e^s N(+\infty) = e^u - e^s$

这就是教科书中所定义的内在价值。

当 $u<s$ ，在 $\tau > 0$ 时：

$\lim_{\tau \to 0} C = \lim_{\tau \to 0} e^uN\Big(\frac{u-s}{\tau} + \frac{\tau}{2}\Big)-e^sN\Big(\frac{u-s}{\tau} - \frac{\tau}{2}\Big) = e^u N(-\infty) - e^s N(-\infty)$

又 $N(-\infty)=0$ ，于是

$\lim_{\tau \to 0} C = e^u N(-\infty) - e^s N(-\infty) = 0$

这种情况下没有内在价值。

当 $u=s$ ，在 $\tau > 0$ 时也没有内在价值。（从上面两种情况，即价差的两个方向求极限，都得到零。）

归纳一下，内在价值为：

$I(u,s)= e^u - e^s, (u\geq s)$

$I(u,s)= 0, (u \leq s)$

教科书中时间价值可以定义为：

$V(\tau, u, s) = C(\tau, u, s) - I(u,s)$

即期权价格减去内在价值的部分。现在看来，更准确的叫法应该是波时价值。由于内在价值与波时无关：

$\frac{dV}{d\tau} = \frac{dC}{d\tau} = e^u \frac{d}{d\tau} N\Big(\frac{u-s}{\tau} + \frac{\tau}{2}\Big)-e^s \frac{d}{d\tau} N\Big(\frac{u-s}{\tau} - \frac{\tau}{2}\Big)$

带入分布公式

$\frac{dV}{d\tau} = \frac{e^u}{\sqrt{2\pi}} \frac{d}{d\tau} \int_{-\infty}^{\frac{u-s}{\tau} + \frac{\tau}{2}} e^{-z^2/2}dz - \frac{e^s}{\sqrt{2\pi}} \frac{d}{d\tau} \int_{-\infty}^{\frac{u-s}{\tau} - \frac{\tau}{2}} e^{-z^2/2}dz$

价差变量

我们把三变量看涨期权公式 $C(u,s,\tau)$ 中的行权价 $s$ 和波时 $\tau$ 固定下来，考虑期权价受到价差 $p = u - s$ 的影响。

$C(p) = e^uN\Big(\frac{p}{\tau} + \frac{\tau}{2}\Big)-e^sN\Big(\frac{p}{\tau} - \frac{\tau}{2}\Big)$

$= e^{p+s}N\Big(\frac{p}{\tau} + \frac{\tau}{2}\Big)-e^sN\Big(\frac{p}{\tau} - \frac{\tau}{2}\Big)$

$= e^s \Big[ e^{p}N\Big(\frac{p}{\tau} + \frac{\tau}{2}\Big)-N\Big(\frac{p}{\tau} - \frac{\tau}{2}\Big) \Big]$

期权交易中的希腊字母 $\Delta$ 代表对冲比率，它本质上是以下导数：

$\frac{dC}{dp} = e^s \frac{d}{dp} \Big[ e^{p}N\Big(\frac{p}{\tau} + \frac{\tau}{2}\Big)-N\Big(\frac{p}{\tau} - \frac{\tau}{2}\Big) \Big]$

$= e^s \Big[ e^{p}N\Big(\frac{p}{\tau} + \frac{\tau}{2}\Big) +e^{p} \frac{d}{dp}N\Big(\frac{p}{\tau} + \frac{\tau}{2}\Big) -\frac{d}{dp} N\Big(\frac{p}{\tau} - \frac{\tau}{2}\Big) \Big]$

注意正态分布公式的导数为

$\frac{dN}{dx}=\frac{1}{\sqrt{2\pi}} \frac{d}{dx} \int_{-\infty}^{x} e^{-z^2/2}dz = \frac{e^{-z^2/2}}{\sqrt{2\pi}}$

于是令

$z_\pm=\Big(\frac{p}{\tau} \pm \frac{\tau}{2}\Big)$

有

$\frac{d}{dp} N\Big(\frac{p}{\tau} \pm \frac{\tau}{2}\Big) = \frac{e^{-z_\pm^2/2}}{\sqrt{2\pi}} \frac{d}{dp}\Big(\frac{p}{\tau} \pm \frac{\tau}{2}\Big) = \frac{e^{-z_\pm^2/2}}{\tau\sqrt{2\pi}}$

得到

$\frac{dC}{dp} = e^s \Big[ e^{p}N\Big(\frac{p}{\tau} + \frac{\tau}{2}\Big) +e^{p} \frac{e^{-z_+^2/2}}{\tau\sqrt{2\pi}} - \frac{e^{-z_-^2/2}}{\tau\sqrt{2\pi}} \Big]$

注意

$\lim_{p \to \pm\infty} z_\pm = \lim_{p \to \pm\infty} \Big(\frac{p}{\tau} \pm \frac{\tau}{2}\Big) = \lim_{p \to \pm\infty} p/\tau = \pm\infty$

$\lim_{p \to \pm\infty} e^{-z_\pm^2/2} = 0$

当价差运动到深度实值时：

$\lim_{p \to +\infty} \frac{dC}{dp} = \lim_{p \to +\infty} e^s \Big[ e^{p} + e^{p} \frac{e^{-z_+^2/2}}{\tau\sqrt{2\pi}} - \frac{e^{-z_-^2/2}}{\tau\sqrt{2\pi}} \Big]$

$= \lim_{p \to +\infty} e^se^p = \lim_{p \to +\infty} e^{s+p} = \lim_{p \to +\infty} e^u = \lim_{p \to +\infty} \frac{de^u}{dp} = 1$

解释为在深度实值时，期权价格的增速等于标的价的增速，期权价格曲线的斜率渐进于1。

当价差运动到深度虚值时：

$\lim_{p \to -\infty} \frac{dC}{dp} = \lim_{p \to -\infty} e^s \Big[ e^{p} + e^{p} \frac{e^{-z_+^2/2}}{\tau\sqrt{2\pi}} - \frac{e^{-z_-^2/2}}{\tau\sqrt{2\pi}} \Big]$

$= \lim_{p \to -\infty} e^se^p = \lim_{p \to -\infty} e^{s+p} = \lim_{p \to - \infty} e^u = \lim_{p \to -\infty} \frac{de^u}{dp} = 0$

解释为在深度虚值时，期权价格曲线的斜率渐进于0。

当价差为零时为在价（ATM）期权：

$\frac{dC}{dp} \Big\vert_{p=0} = e^s \Big[ e^{p}N\Big(\frac{p}{\tau} + \frac{\tau}{2}\Big) +e^{p} \frac{e^{-z_+^2/2}}{\tau\sqrt{2\pi}} - \frac{e^{-z_-^2/2}}{\tau\sqrt{2\pi}} \Big]$

$= e^s \Big[ N\Big(\frac{\tau}{2}\Big) + \frac{e^{-z_+^2/2}}{\tau\sqrt{2\pi}} - \frac{e^{-z_-^2/2}}{\tau\sqrt{2\pi}} \Big] = e^s \Big[ N\Big(\frac{\tau}{2}\Big) + \frac{e^{-z_+^2/2} - e^{-z_-^2/2}}{\tau\sqrt{2\pi}} \Big]$

$= e^s N\Big(\frac{\tau}{2}\Big)$

我们将使用R进行分析。您应该已经安装了R和RStudio。我建议您安装Microsoft R Open，执行程序速度更快。Quantmod是提供技术分析的重要R包。

课程

R语言数据分析挖掘必知必会

从数据获取和清理开始，有目的的进行探索性分析与可视化。让数据从生涩的资料，摇身成为有温度的故事。

立即参加 ➜

Black Scholes股票期权定价公式

Black Scholes期权定价公式作了一些假设。首先是市场没有套利。这意味着不可能有价格差异。第二个假设是基础资产价格遵循布朗运动。第三个假设表明基础股票不支付任何股息。第四个假设是不涉及交易成本，并且可以以任何分数进行基础股票的买卖。最后一个假设是我们知道短期利率，并且该利率随时间是恒定的。现在，我们不需要详细讨论如何数学公式推导该公式。当我们知道用于计算股票期权价格的不同参数时，将使用R来计算股票期权价格。下面我们使用R来计算3个月到期的Apple AAPL股票看涨期权价格。苹果AAPL股票价格为130美元，股票期权合约行使价为140美元。

> library(fOptions)
Loading required package: timeDate
Loading required package: timeSeries
Loading required package: fBasics
 
> GBSOption(TypeFlag = "c", S = 130, X =140, Time = 1/4, r = 0.02, 
+           sigma = 0.22, b = 0.02)
 
Title:
 Black Scholes Option Valuation 
 
Call:
 GBSOption(TypeFlag = "c", S = 130, X = 140, Time = 1/4, r = 0.02, 
     b = 0.02, sigma = 0.22)
 
Parameters:
          Value:
 TypeFlag c     
 S        130   
 X        140   
 Time     0.25  
 r        0.02  
 b        0.02  
 sigma    0.22  
 
Option Price:
 2.382111 
 
Description:
 Sun May 07 18:12:25 2017

首先我们加载fOptions库，c表示看涨期权.S是股票价格，即每股130美元。X是股票行使价，每股140美元。短期利率为2％。隐含波动率假设为22％。苹果股票的看涨期权价格为2.38美元。这就是它的工作方式。苹果目前的股价为每股130美元。我们购买看涨期权。我们认为苹果股票的价格将会上涨，因此我们购买了看涨期权为140美元的苹果股票3个月到期的看涨期权。如果价格超过140美元，我们可以每股140美元的价格购买AAPL股票。目前，苹果股票的交易价格为每股148美元。因此，您可以看到我们可以便宜地购买Apple股票。我们将以140美元的价格行使苹果股票看涨期权合约，然后以148美元的价格在市场上出售股票，从而实现每股8美元的利润。由于价格是2美元。每100股38股，我们获得了可观的利润。假设我们的行使价为135美元。

 
Title:
 Black Scholes Option Valuation 
 
Call:
 GBSOption(TypeFlag = "c", S = 130, X = 135, Time = 1/4, r = 0.02, 
     b = 0.02, sigma = 0.22)
 
Parameters:
          Value:
 TypeFlag c     
 S        130   
 X        135   
 Time     0.25  
 r        0.02  
 b        0.02  
 sigma    0.22  
 
Option Price:
 3.88815 
 
Description:
 Sun May 07 18:22:29 2017

最受欢迎的见解

1.用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)的应用

2.R语言GARCH-DCC模型和DCC（MVT）建模估计

3.R语言实现 Copula 算法建模依赖性案例分析报告

4.R语言COPULAS和金融时间序列数据VaR分析

5.R语言多元COPULA GARCH 模型时间序列预测

6.用R语言实现神经网络预测股票实例

7.r语言预测波动率的实现：ARCH模型与HAR-RV模型

8.R语言如何做马尔科夫转换模型markov switching model

9.matlab使用Copula仿真优化市场风险

在这种情况下，股票期权的价格提高到了$ 3.88。现在，如上所述，我们不需要知道如何得出Black Scholes期权定价公式。我们只需要在公式中插入不同的参数，例如看涨/卖出期权，股票价格，执行价格，短期利率，隐含波动率等。现在的问题是我们没有任何方法可以计算隐含波动率。我们只是假设了隐含波动率公式。

我们还可以计算看跌期权的价格。使用R时也非常容易。以下是看跌期权价格的计算。我们在公式中将c更改为p。苹果股价为130美元。看跌期权的行使价为135美元。有效期为3个月。短期利率为2％。隐含波动率为22％。

> GBSOption(TypeFlag = "p", S = 130, X =135, Time = 1/4, r = 0.02, sigma
+           = 0.22, b = 0.02)@price
[1] 8.214834

现在，如上所述，Black Scholes期权定价公式很大程度上取决于隐含波动率。隐含波动率是我们所不知道的。因此，实际上我们不能使用此Black Scholes股票期权价格公式。在大多数情况下，我们使用相反的公式。我们在公式中插入股票期权价格并计算隐含波动率。我们可以使用GARCH模型来计算波动率。

Cox-Ross-Rubinstein股票期权定价公式

Cox-Ross-Rubinstein公式也称为CRR公式，与Black Scholes股票期权定价公式不同。CRR公式中的基本假设是标的股票价格遵循离散的二项分布。这意味着股票价格在每个时期要么上升一定量，要么下降一定量。二叉树正在重组。这意味着在两个时期内，价格可以先涨后跌，或者在相同的最终价格下涨跌。以下是使用与Black Scholes公式相同的行使价，隐含波动率和短期利率来计算Apple股票期权价格。

> 
[1] 4.033903
>
[1] 8.360588

您可以看到使用Cox-Ross-Rubinstein公式的期权价格与Black Scholes公式相似但不相同，现在无需对CRR公式进行复杂的数学推导。我们还可以绘制上述看涨期权公式以及看跌期权公式二项式树3个周期。以下是看涨期权二项式树的代码。

通过将ce更改为pe，我们还可以绘制看跌期权二叉树。以下是看涨期权二叉树图。

以下是看跌期权二叉树。

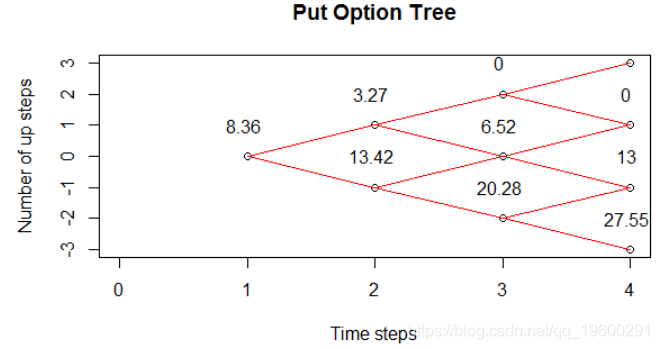
现在您看到了两个公式之间的期权价格差异。价格差异不大。Black Scholes计算的看涨期权价格为3.88美元，而Cox-Ross-Rubinstein公式计算的看涨期权价格为4.03美元。差别不是很大，但确实存在。这是由于两个公式的数学推导不同。在Black Scholes公式中，我们假设一个连续的随机公式，而在Cox-Ross-Rubinstein公式中，我们假设一个离散的二项式公式。W可以通过减少Cox-Ross-Rubinstein公式中的时间步长来减少价格差异。

如何计算期权？

希腊人衡量期权合约对不同市场因素的敏感性。例如，delta是对基础股票价格的敏感性。Gamma是对基础股票价格变化的敏感性。您可以将伽玛三角洲称为三角洲。Theta对时间敏感，而rho对无风险利率敏感。最后，vega是对隐含波动率的敏感度。用数学术语来说，所有希腊语都是偏导数，用于衡量某些参数的变化率。下面我们使用R计算。

> 
      delta       gamma        vega       theta         rho 
  0.4041424   0.0270888  25.1790377 -12.0517840  12.1625922

您可以看到R在计算时非常快。跨距交易是重要的期权交易策略。我们通过同时购买看跌期权和看涨期权来构造一个跨步。以下是跨度的增量计算。

 
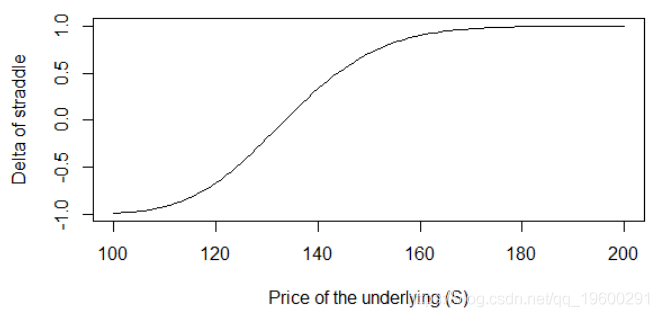
> plot(100:200, rowSums(straddles), type='l', 
+      xlab='Price of the underlying (S)', ylab = 'Delta of straddle')

计量经济学是许多交易者都不知道的重要主题。以下是使用苹果股票看跌期权和看涨期权的跨式期权构建的增量图。

可下载资源

关于作者

Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。

本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。

非常感谢您阅读本文，如需帮助请联系我们！

R语言Black Scholes和Cox-Ross-Rubinstein期权定价模型案例

原始BSM

对数化处理

无风险收益率的简化

概率项的对称化

时间极限

价差变量

Black Scholes股票期权定价公式

Cox-Ross-Rubinstein股票期权定价公式

如何计算期权？

相关文章

R语言Black Scholes和Cox-Ross-Rubinstein期权定价模型案例

原始BSM

对数化处理

无风险收益率的简化

概率项的对称化

时间极限

价差变量

Black Scholes股票期权定价公式

Cox-Ross-Rubinstein股票期权定价公式

如何计算期权？

相关文章

关注有关新文章的微信公众号