在生态与生物学研究中，数据常呈现复杂结构特征。例如不同种群、采样点或时间序列的观测数据间往往存在相关性。
传统线性模型在处理这类非独立数据时存在局限性，
而混合效应模型通过同时纳入固定效应与随机效应，
为解决此类问题提供了有效方案。
本文以龙类智力研究为例，探讨混合效应模型的构建与应用。
研究数据来自龙类智力测试，包含体长（bodyLength）与测试得分（testScore）等变量，采集自8个山脉3个采样点。
数据探索与预处理
×
基本概念：混合效应模型是一种统计模型，用于分析具有复杂数据结构的数据，能同时考量固定效应和随机效应。固定效应是对群体或总体具有一致作用的变量，其参数在不同样本中保持不变，反映的是总体趋势，类似于传统线性回归模型中的自变量，可理解为研究者关注的主要影响因素 ，如实验中的实验条件、词频、语言水平等。随机效应是对个体或子样本有不同作用的变量，其参数会在不同样本中变化，用于描述来自不同实验单位、观察组或时间点的变异，可用来捕捉数据中由组间差异引起的变动，比如个体之间的差异、不同湖泊之间的差异等。
数学表达：线性混合效应模型的标准形式可表示为
y=Xβ+Zb+ϵ
。其中
y
是响应向量（即因变量观测数据）；
X
是与固定效应参数
β
相关的设计矩阵；
β
是固定效应系数向量；
Z
是与随机效应参数
b
相关的设计矩阵；
b
是随机效应向量；
ϵ
是误差项。
适用场景：该模型在诸多领域应用广泛，主要用于处理具有层次结构（如学生嵌套在班级、班级嵌套在学校）、组间关联或重复测量的数据（如在不同时间点对同一组个体进行观察）。比如在生物统计学中分析不同环境下生物的生长情况，社会科学中研究不同地区人群的行为模式，心理学中处理被试的个体差异和实验材料特性等问题。
优势：相比线性回归模型，它能够处理更复杂的数据结构，分析群体和个体差异；和广义线性模型（glm）相比，还可以处理随机效应。此外，它还可以处理缺失数据和不平衡设计，对于重复测量数据，能够考虑时间相关性，充分利用数据中的所有信息，提升分析效率，使结果更准确，避免因遗漏信息而产生偏差，降低出现伪阳性结果的风险。
劣势：计算复杂度较高，需要专门的软件和算法进行估计；随机效应的选择和模型设定可能存在主观性；结果的解释和推断可能比较复杂。
在 R 语言中的使用：使用 lmer 函数构建模型，语法通常为lmer(因变量 ~ 固定效应 + (随机效应结构)， data = 数据集) 。例如model<-lmer(algae_biomass~ph+phosphate+(1|lake),data=algae_data)，表示基于 algae_data 数据集，构建一个因变量为 algae_biomass ，固定效应为 ph 和 phosphate，随机效应为 lake（湖泊）的混合效应模型。使用summary(模型对象)可以查看模型摘要，从而了解固定效应的系数、标准误差、t 值、p 值，以及随机效应的方差等信息，以评估变量的影响和模型的拟合效果。
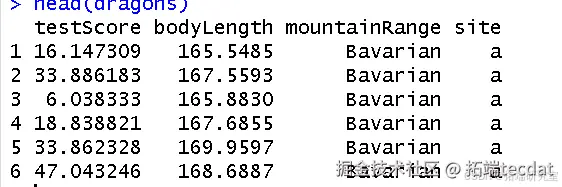
通过标准化处理体长变量：
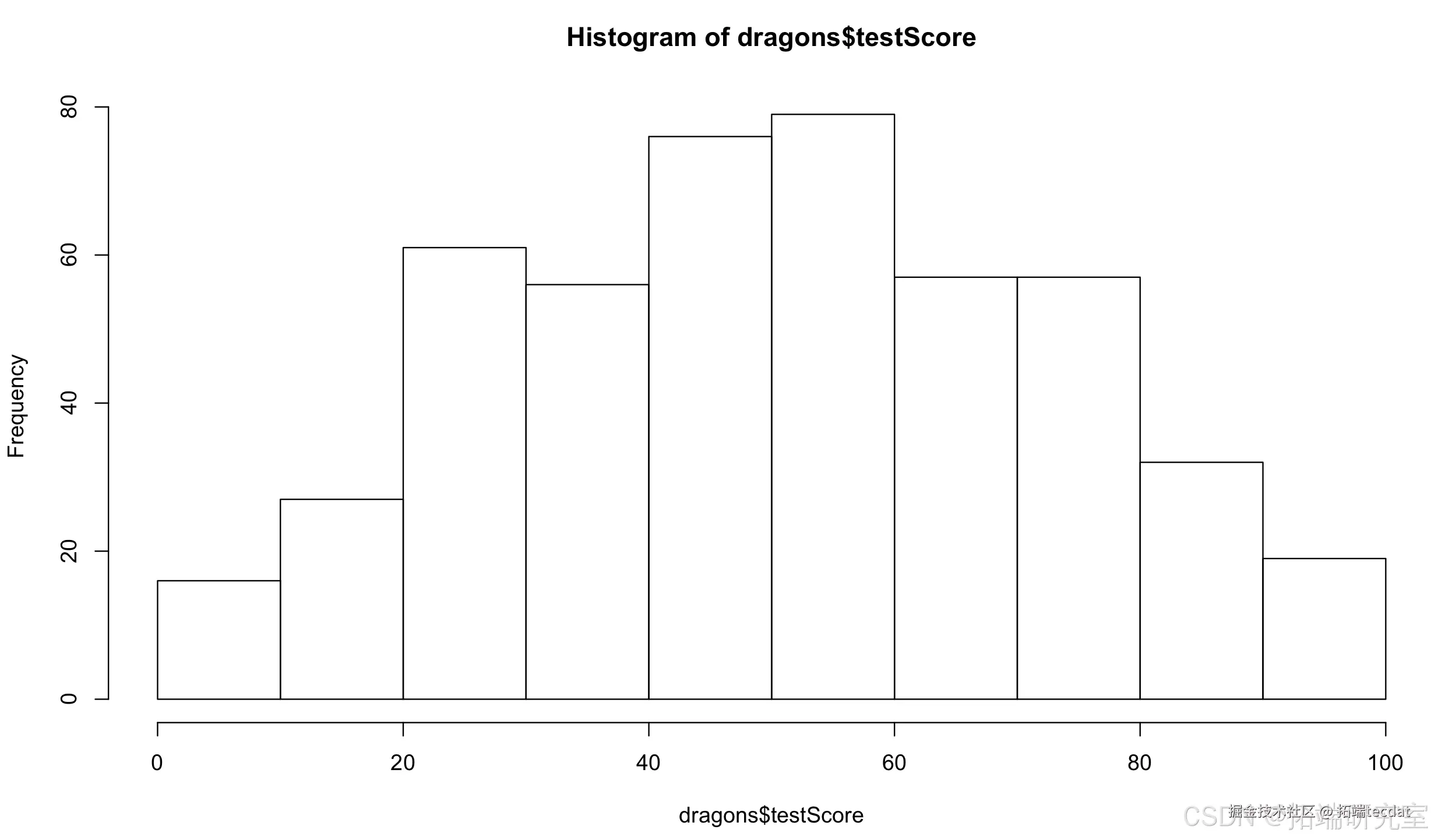
dradat$length <a(dag_datodyLeng)直方图显示测试得分近似正态分布（图1），符合线性模型假设。
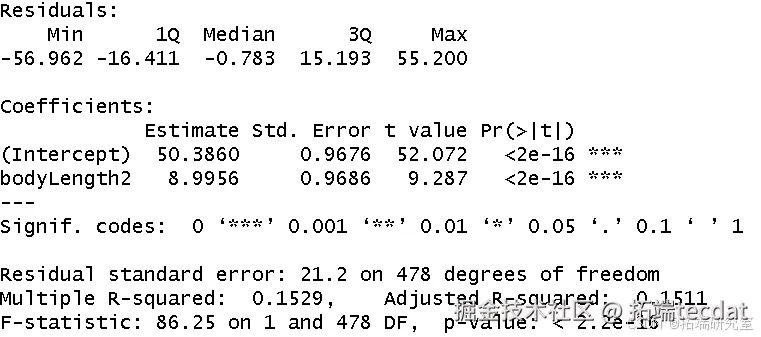
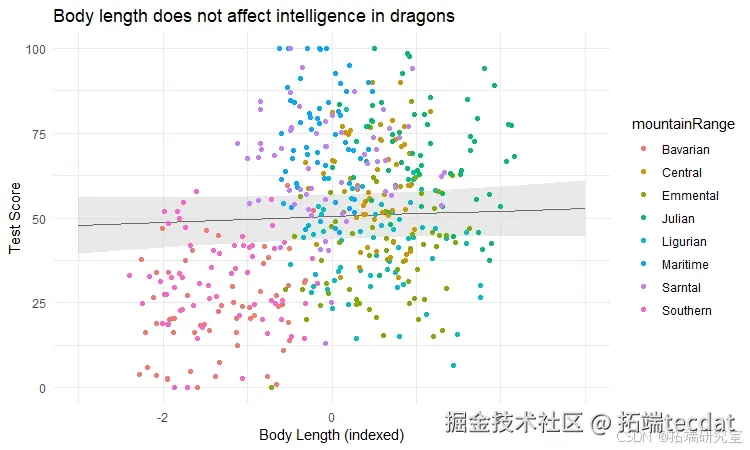
模型显示体长对测试得分有显著正向影响（p<0.05）。但散点图揭示不同山脉间数据存在明显异质性（图2），提示观测值可能存在非独立性。
进一步分析发现，不同山脉间测试得分存在显著差异（图3），说明传统模型忽略了数据的层级结构，可能导致结果偏差。
想了解更多关于模型定制、辅导的信息？
混合效应模型构建
引入山脉作为随机效应：
library(lme data=drta) summary(mixed_model)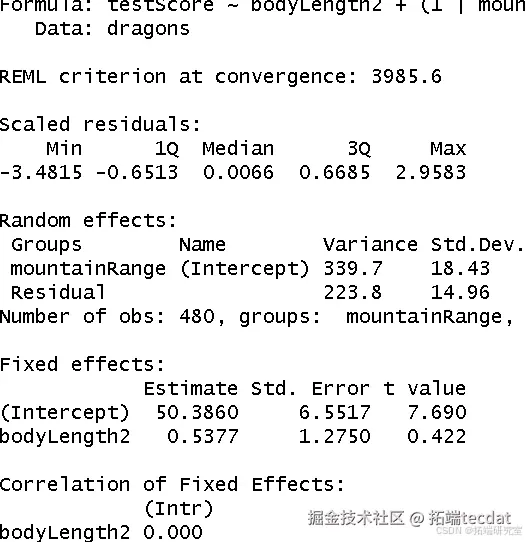
模型结果显示，体长的影响不再显著（p>0.05），表明原线性模型高估了体长效应。随机效应分析表明，山脉间差异解释了约60%的剩余方差（339.7/(339.7+223.8)）。
为处理嵌套结构（采样点嵌套于山脉），创建显式嵌套变量：
dragota$mountainRange, dragon_data$site))改进模型：
nesteinRange) + (1|site_id), data=dragon_data)模型可视化与结果解释
利用ggeffects包绘制预测曲线：
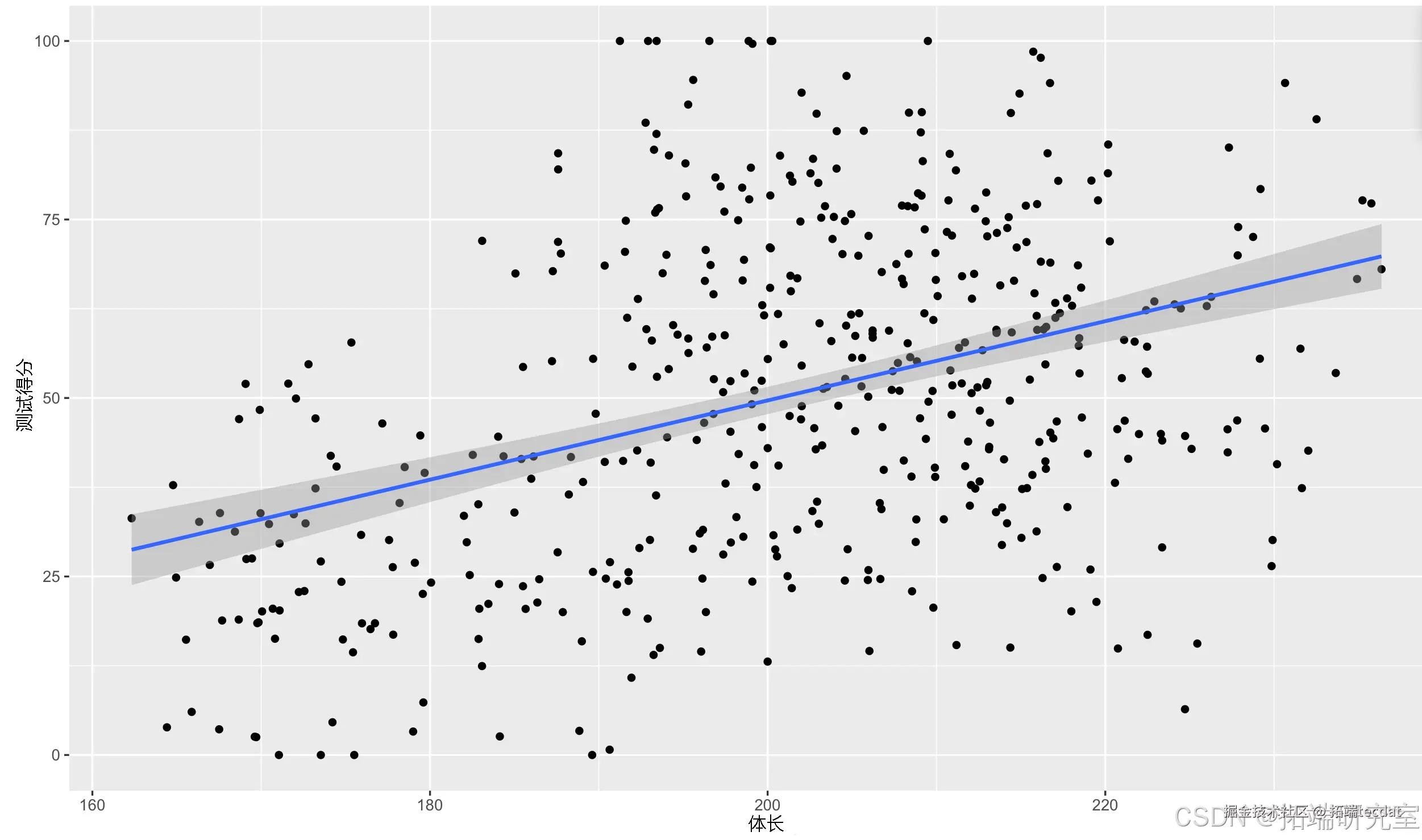
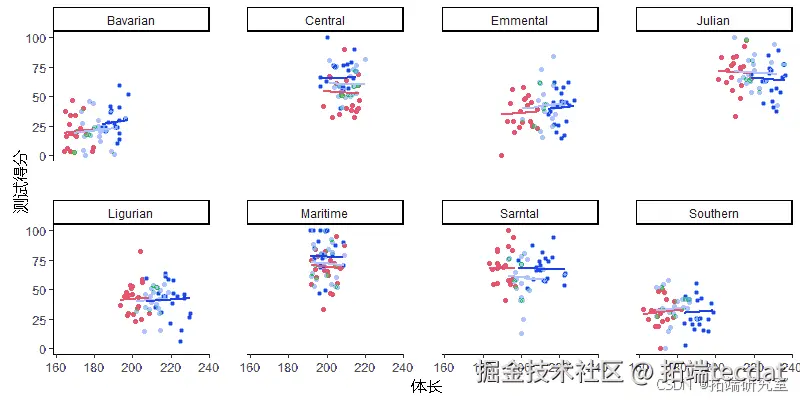
library(ggeffects) model_pred <- ggpredict(nestedata, aes(std_length, testScore, color=mountainRange))结果显示体长对测试得分无显著影响（图4），验证了混合效应模型的有效性。
随机斜率模型扩展
当不同山脉间可能存在异质关系时，可构建随机斜率模型：
slope_model <- lmer(testScore ~ std_length + (1+std_length|mountainRange), data=dragon_data)可视化结果显示不同山脉的回归斜率存在差异（图5），表明模型灵活性提升。
随时关注您喜欢的主题
模型诊断与优化
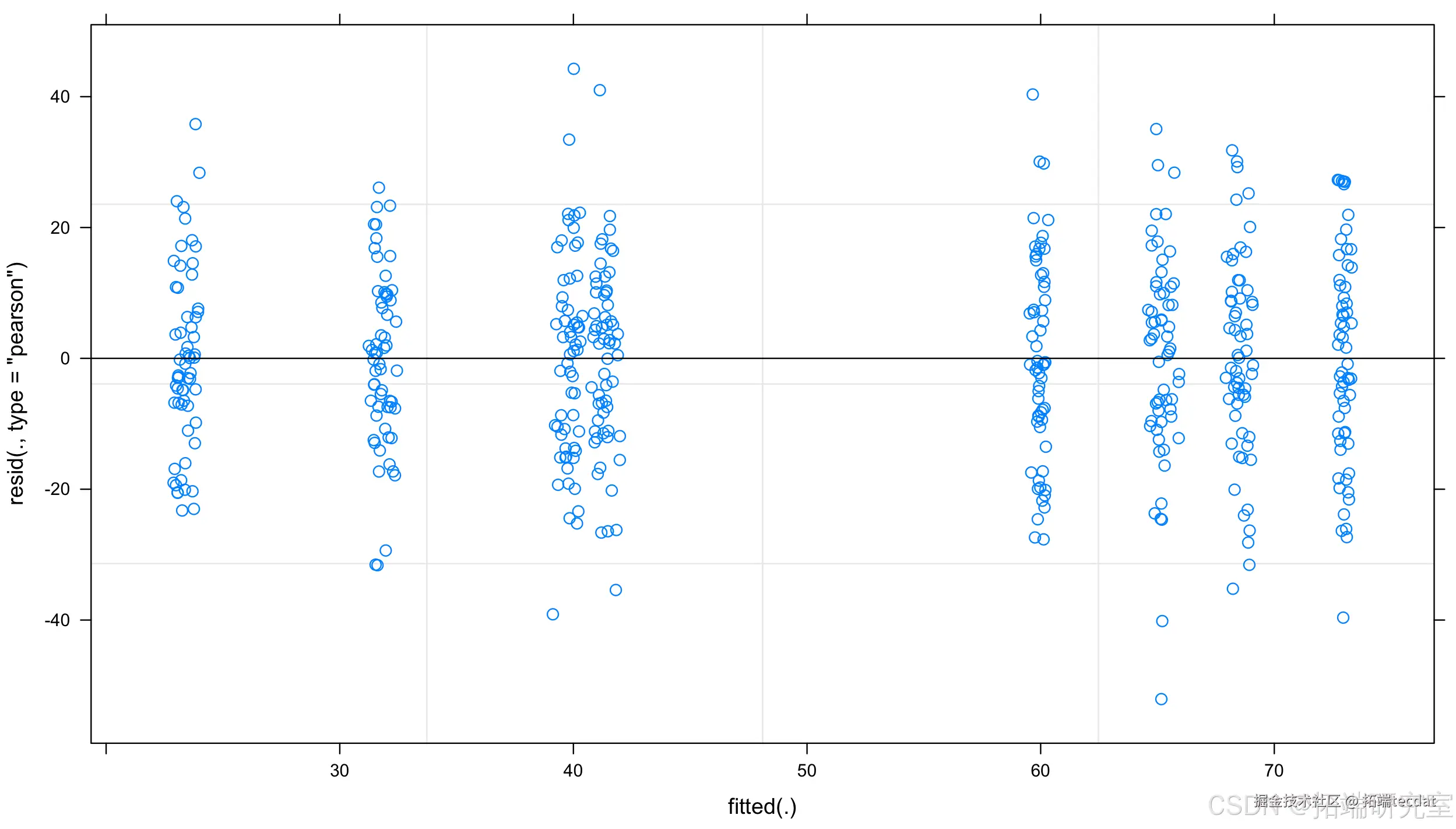
通过残差分析验证模型假设：
plot(nested_model, which=1) qqnorm(resid(nested_model))残差分布基本符合正态性假设（图6），表明模型拟合良好。
结论与建议
本研究通过混合效应模型有效解决了传统方法无法处理的层级数据问题，揭示了体长与龙类智力间的真实关系。研究结果表明：
- 数据层级结构必须纳入模型考量
- 随机效应的合理选择对结果解释至关重要
- 模型可视化是验证假设的重要手段
未来研究可进一步探索广义混合效应模型在非线性数据中的应用，以及模型参数的贝叶斯估计方法。
每日分享最新报告和数据资料至会员群
关于会员群
- 会员群主要以数据研究、报告分享、数据工具讨论为主；
- 加入后免费阅读、下载相关数据内容，并同步海内外优质数据文档；
- 老用户可九折续费。
- 提供报告PDF代找服务
非常感谢您阅读本文，如需帮助请联系我们！
Python梯度提升模型GBM生态学研究：SFS、RandomizedSearchCV预测黑腿蜱种群分布丰度可视化
Python线性混合效应回归LMER分析大鼠幼崽体重数据、假设检验可视化
R语言广义线性混合模型GLMMs在生态学中应用可视化2实例合集|附数据代码
R语言生态学种群空间点格局分析：聚类泊松点过程对植物、蚂蚁巢穴分布数据可视化
