在大数据的趋势下,我们经常需要做预测性分析来帮助我们做决定。
最近我们被客户要求撰写关于时间序列的研究报告,包括一些图形和统计输出。其中一个重要的事情是根据我们过去和现在的数据来预测未来。这种方法我们通常被称为预测。
一个事件的可预测性取决于多个因素,这些因素可能涉及数据的可用性、影响因素的复杂性、历史模式的稳定性以及所采用预测方法的准确性等。在您提到的三种情况中,对未来的电力需求、呼叫中心的呼叫量以及库存需求进行预测,各自的可预测性也受不同因素的影响。
对于电力需求预测,关键因素可能包括历史电力消费数据的趋势分析、经济指标(如GDP、工业生产指数、人口增长等)的关联分析,以及政策导向(如节能减排政策)的影响。这些因素可以提供对未来电力需求的洞察,但也可能受到经济波动、政策变化以及技术进步等多种不确定性的影响。
可下载资源
作者

许多情况下都需要预测:决定是否在未来五年内再建一座发电站需要对未来的需求进行预测;安排下周呼叫中心的工作人员需要对呼叫量进行预测;储备库存需要对库存需求进行预测。一个事件的可预测性取决于几个因素,包括。
- 我们对造成这种情况的因素了解得如何。
- 有多少数据可用。
- 预测是否能影响我们试图预测的事物。
ARIMA
差分整合自回归移动平均模型(ARIMA)(p,d,q)是自回归(AR)、移动平均(MA)和自回归移动平均(ARMA)模型的扩展版本。ARIMA模型是应用于时间序列问题的模型。ARIMA将三种类型的建模过程结合到一个建模框架中。
视频
时间序列分析模型 ARIMA-ARCH GARCH模型分析股票价格数据
视频
在Python和R语言中建立EWMA,ARIMA模型预测时间序列
- I:差分是用d表示的。它告诉我们在连续的观察样本中,被差分的序列对于原始序列的变化数量。
- AR:自回归用p表示,它告诉我们为适应平稳序列的AR过程所需的滞后期数。ACF和PACF帮助我们确定AR过程的最佳参数集。
- MA:移动平均阶数用q表示。它告诉我们要回归的序列中的误差项的数量,以便将差分的AR过程残差减少为白噪声。
关于ARIMAX
ARIMAX或回归ARIMA是ARIMA模型的一个扩展。在预测中,这种方法也涉及自变量。ARIMAX模型表示输出时间序列由以下部分组成:自回归(AR)部分,移动平均(MA)部分,差分整合(I)部分,以及属于外生输入(X)的部分。外生部分(X)反映了将外生输入的现值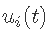 和过去值
和过去值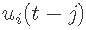 包括到ARIMAX模型中。
包括到ARIMAX模型中。
多元回归模型公式:
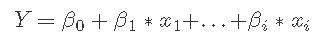
其中Y是xi预测变量的因变量,ε通常被认为是一个不相关的误差项(即是白噪声)。我们考虑了诸如Durbin-Watson检验等检验方法来评估ε是否有显著的相关性。我们将在方程中用nt代替ε。误差序列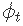 被假定为遵循ARIMA模型。例如,如果 nt 遵循一个 ARIMA(1,1,1)模型,我们可以写成
被假定为遵循ARIMA模型。例如,如果 nt 遵循一个 ARIMA(1,1,1)模型,我们可以写成
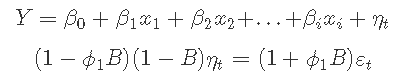
其中εt是一个白噪声序列。ARIMAX模型有两个误差项,一个是回归模型的误差,我们用jt表示,另一个是ARIMA模型的误差,我们用εt表示。只有ARIMA模型的误差被认为是白噪声。
实例探究
我们将使用经济序列数据。
数据是一个五个季度的经济序列,包含以下数字变量:季度失业率、国民生产总值、消费、政府投资和私人投资。有161个观测点。
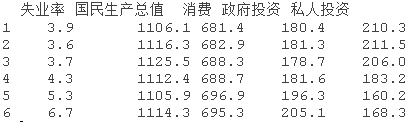
季节性成分已经从数据中去除。集中在失业率(Ut)、国民生产总值(Gt)和消费(Ct)上,首先对每个序列进行记录,然后去掉线性趋势,对数据拟合一个向量ARMA模型。也就是说,对xt=(x1t,x2t,x3t)t拟合一个向量ARMA模型,例如,x1t=log(Ut)-β0^-β1^t,其中β0^和β1^是log(Ut)对时间t的回归的最小二乘估计。对残差运行一套完整的诊断方法。
数据探索
grid.arrange(p1,p2,p3,ncol=2)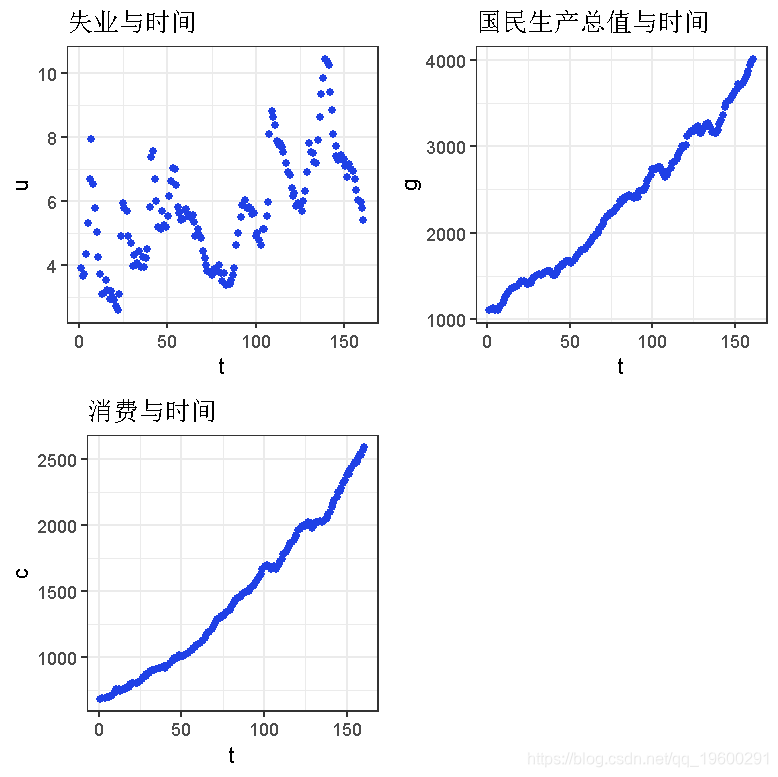
从图中可以看出,国民生产总值和消费可以作为回归使用。我们可以用时间、国民生产总值和消费来预测失业率。
ARIMAX模型拟合
summary(varma)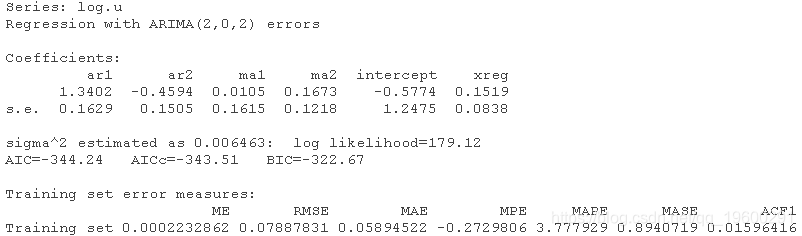
随时关注您喜欢的主题
plot(df,aes(t,res))+line(col=colpla\[2\])
acf\_pacf(res\_= acf(x, plot= F)
, label= "ACF")
plot(df, aes(x=res)) +
histogram(aes(y=..density..)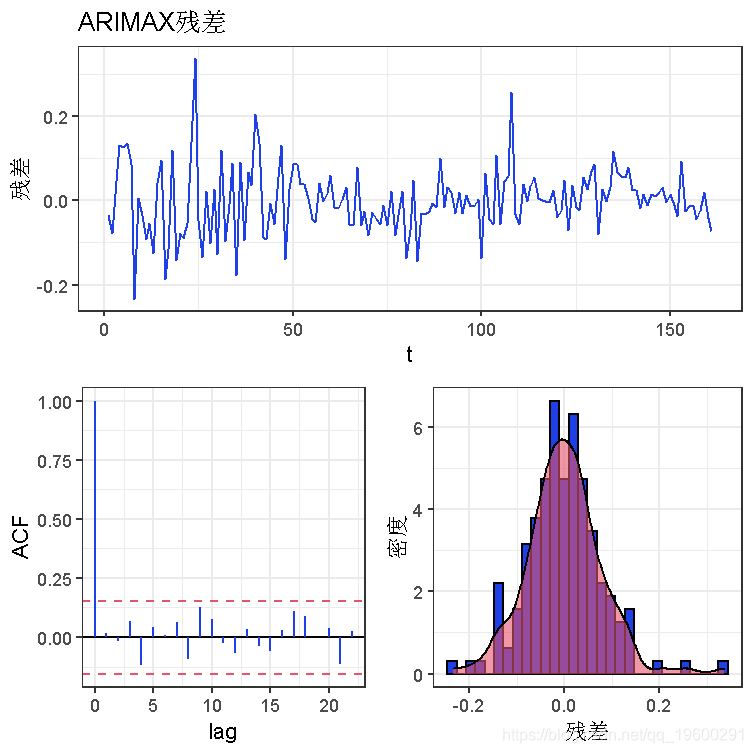
我们的残差在大多数情况下是正态分布的,ACF图中没有明显的尖峰。Ljung-Box检验在5%的水平上有0.05297的p值,所以数据是独立分布的,在任何滞后期都没有明显的自相关。这是一个理想的结果。

想了解更多关于模型定制、咨询辅导的信息?
预测
我们随机生成log(g)和log(c)的向量,作为我们预测模型的输入值。两个向量的长度都是8,所以我们的目标是预测未来8个季度的log(u)值。
请注意,对于多个回归因子,我们必须将这些向量合并成一个矩阵,以便我们进行预测工作。
forecast(m,x=logfc+logc )
plot(yfor)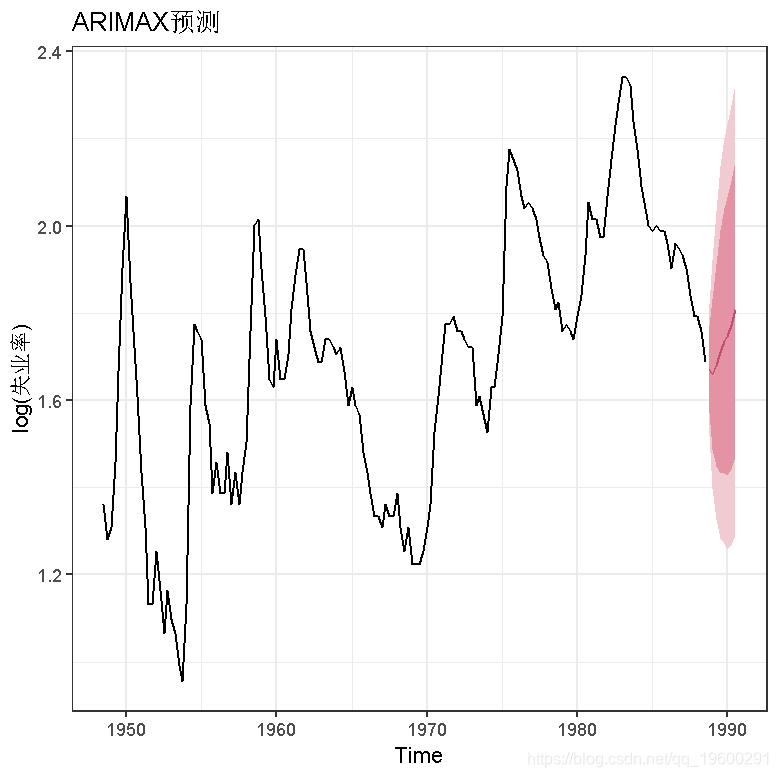
ARIMA模型
通过使用ARIMA,我们只根据连续的时间数据来预测未来。它忽略了可能影响消费变化的其他因素。
要使用ARIMAX模型,有几个可能的优点和缺点。
ARIMAX优点缺点
优点
使用ARIMAX的好处是我们可以将回归和时间序列部分结合在一个模型中,命名为ARIMAX。与回归模型或ARIMA模型相比,这个模型可以优化我们的误差。
缺点
一个缺点是,协变量系数很难解释。斜率的值不是xt增加1时对Yt的影响(就像回归中那样)。方程右侧存在因变量的滞后值,这意味着斜率β只能以因变量以前的值为条件进行解释,这很不直观。
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!


 Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究
Python对2028奥运奖牌预测分析:贝叶斯推断、梯度提升机GBM、时间序列、随机森林、二元分类教练效应量化研究 视频讲解|Python图神经网络GNN原理与应用探索交通数据预测
视频讲解|Python图神经网络GNN原理与应用探索交通数据预测 Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
Python用Transformer、SARIMAX、RNN、LSTM、Prophet时间序列预测对比分析用电量、零售销售、公共安全、交通事故数据
