最近我们被客户要求撰写关于集成模型的研究报告。本文我们使用4个时间序列模型对每周的温度序列建模。
第一个是通过auto.arima获得的，然后两个是SARIMA模型，最后一个是Buys–Ballot方法。
可下载资源
我们使用以下数据
k=620
n=nrow(elec)
futu=(k+1):n
y=electricite$Load[1:k]
plot(y,type="l")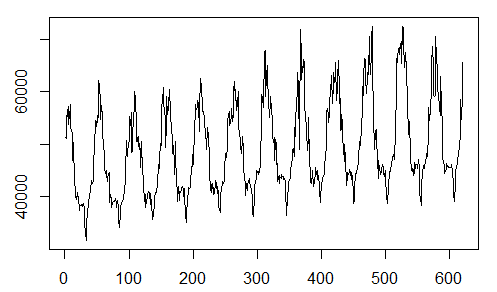
集成学习是一种机器学习范式。在集成学习中，我们会训练多个模型（通常称为「弱学习器」）解决相同的问题，并将它们结合起来以获得更好的结果。最重要的假设是：当弱模型被正确组合时，我们可以得到更精确和/或更鲁棒的模型。
在集成学习理论中，我们将弱学习器（或基础模型）称为「模型」，这些模型可用作设计更复杂模型的构件。在大多数情况下，这些基本模型本身的性能并不是非常好，这要么是因为它们具有较高的偏置（例如，低自由度模型），要么是因为他们的方差太大导致鲁棒性不强（例如，高自由度模型）。
集成方法的思想是通过将这些弱学习器的偏置和/或方差结合起来，从而创建一个「强学习器」（或「集成模型」），从而获得更好的性能。
组合弱学习器
为了建立一个集成学习方法，我们首先要选择待聚合的基础模型。在大多数情况下（包括在众所周知的 bagging 和 boosting 方法中），我们会使用单一的基础学习算法，这样一来我们就有了以不同方式训练的同质弱学习器。
这样得到的集成模型被称为「同质的」。然而，也有一些方法使用不同种类的基础学习算法：将一些异质的弱学习器组合成「异质集成模型」。
很重要的一点是：我们对弱学习器的选择应该和我们聚合这些模型的方式相一致。如果我们选择具有低偏置高方差的基础模型，我们应该使用一种倾向于减小方差的聚合方法；而如果我们选择具有低方差高偏置的基础模型，我们应该使用一种倾向于减小偏置的聚合方法。
这就引出了如何组合这些模型的问题。我们可以用三种主要的旨在组合弱学习器的「元算法」：
bagging，该方法通常考虑的是同质弱学习器，相互独立地并行学习这些弱学习器，并按照某种确定性的平均过程将它们组合起来。boosting，该方法通常考虑的也是同质弱学习器。它以一种高度自适应的方法顺序地学习这些弱学习器（每个基础模型都依赖于前面的模型），并按照某种确定性的策略将它们组合起来。stacking，该方法通常考虑的是异质弱学习器，并行地学习它们，并通过训练一个「元模型」将它们组合起来，根据不同弱模型的预测结果输出一个最终的预测结果。非常粗略地说，我们可以说 bagging 的重点在于获得一个方差比其组成部分更小的集成模型，而 boosting 和 stacking 则将主要生成偏置比其组成部分更低的强模型（即使方差也可以被减小）。
我们开始对温度序列进行建模（温度序列对电力负荷的影响很大）
y=Temp
plot(y,type="l")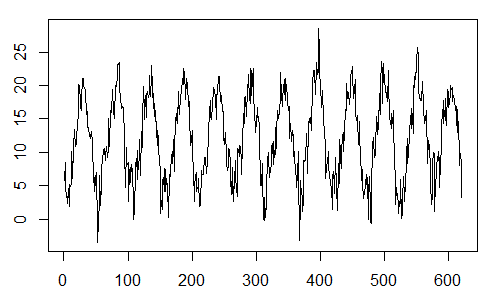
abline(lm(y[ :k]~y[( :k)-52]),col="red")
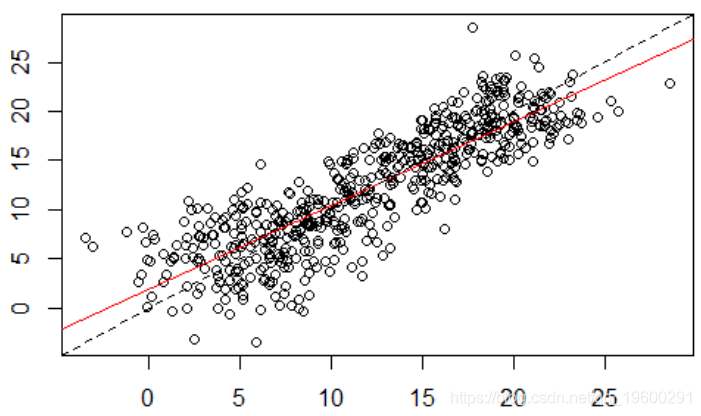
时间序列是自相关的，在52阶
acf(y,lag=120)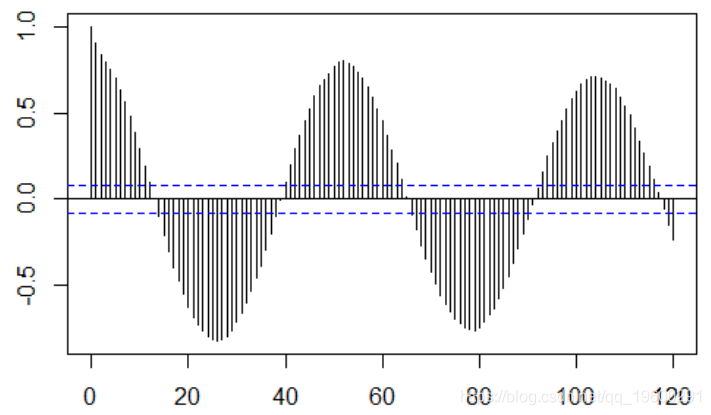 
model1=auto.arima(Y)
acf(residuals(model1),120)
我们将这个模型保存在工作空间中，然后查看其预测。让我们在这里尝试一下SARIMA
arima(Y,order = c(0,0,0),
seasonal = list(order = c(1,0,0)))
然后让我们尝试使用季节性单位根
Z=diff(Y,52)
arima(Z,order = c(0,0,1),
seasonal = list(order = c(0,0,1)))
然后，我们可以尝试Buys–Ballot模型
lm(Temp~0+as.factor(NumWeek),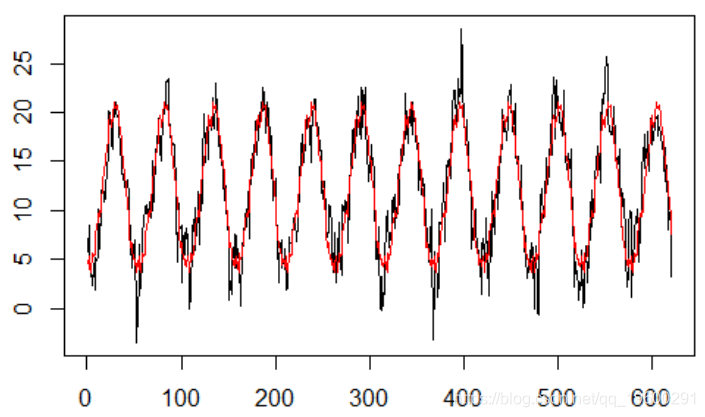 
对模型进行预测
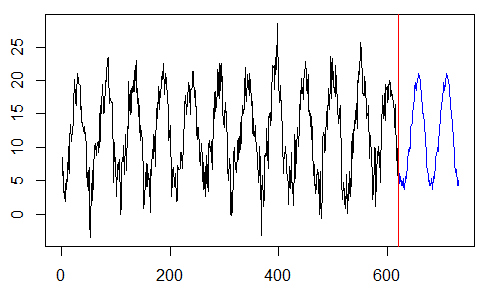
plot(y,type="l",xlim=c(0,n )
abline(v=k,col="red")
lines(pre4,col="blue")
plot(y,type="l",xlim=c(0,n))
abline(v=k,col="red")
plot(y,type="l",xlim=c(0,n))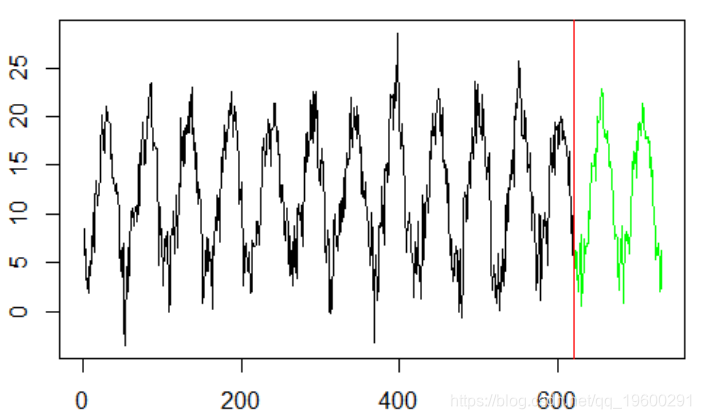 
plot(y,type="l",xlim=c(0,n))
abline(v=k,col="red")
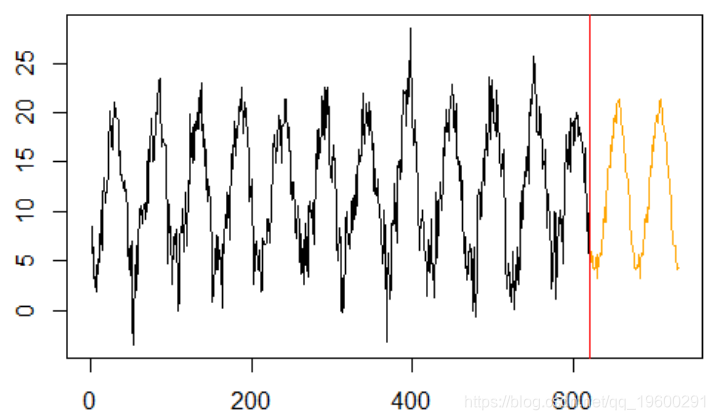
最后比较4个模型的结果
lines( MODEL$y1,col="
lines( MODEL$y2,col="green")
lines( MODEL$y3,col="orange")
lines( MODEL$y4,col="blue")
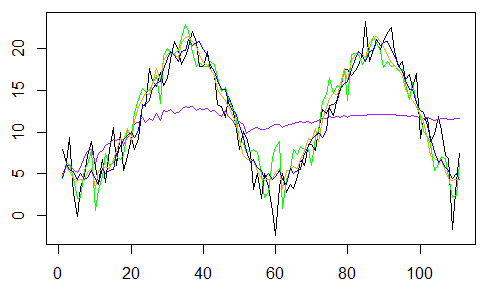
然后，我们可以尝试加权平均值来优化模型，而不是找出四个中的哪一个模型是“最优”，y ^ T = ∑iωiy ^ t（i）其中ω=（ωi），ω1+ … +ωk= 1。然后，我们想要找到“最佳”权重。我们将在第一个m值上校准我们的四个模型，然后比较下111个值（和真实值）的预测组合，
我们使用前200个值。
然后，我们在这200个值上拟合4个模型
然后我们进行预测
y1=predict(model1,n.ahead = 111)$pred,
y2=predict(model2,n.ahead = 111)$pred,
y3=predict(model3,n.ahead = 111)$pred,
y4=predict(model4,n.ahead = 111)$pred+
为了创建预测的线性组合，我们使用
a=rep(1/4,4)
y_pr = as.matrix(DOS[,1:4]) %*% a
随时关注您喜欢的主题
因此，我们可视化这4个预测，它们的线性组合（带有等权重）及其观察值
为了找到权重的“最佳”值，最小化误差平方和，我们使用以下代码
function(a) sum( DONN[,1:4 %*% a-DONN[,5 )^2 我们得到最优权重
optim(par=c(0,0,0),erreur2)$par 然后，我们需要确保两种算法的收敛性：SARIMA参数的估计算法和权重参数的研究算法。
if(inherits(TRY, "try-error") arima(y,order = c(4,0,0)
seasonal = list(order = c(1,0,0)),method="CSS")
然后，我们查看权重随时间的变化。
获得下图，其中粉红色的是Buys-Ballot，粉红色的是SARIMA模型，绿色是季节性单位根，
barplot(va,legend = rownames(counts)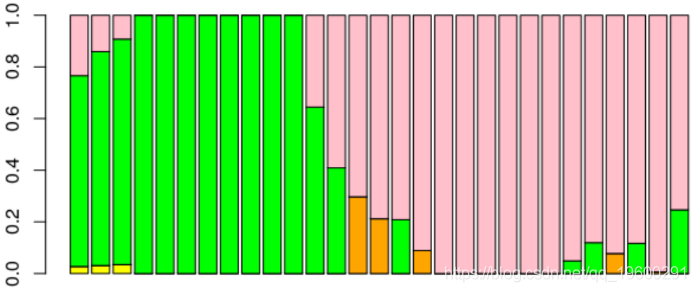 
我们发现权重最大的模型是Buys Ballot模型。
可以更改损失函数，例如，我们使用90％的分位数，
tau=.9
function(e) (tau-(e<=0))*e
在函数中，我们使用
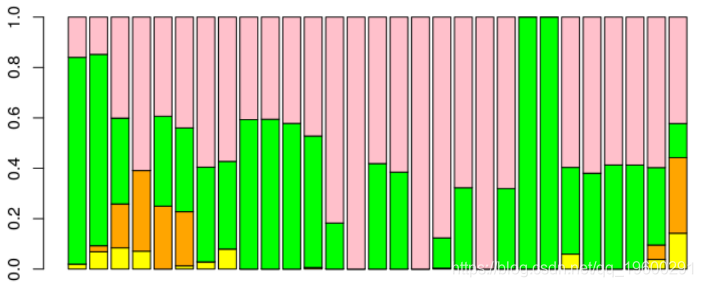
这次，权重最大的两个模型是SARIMA和Buys-Ballot。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
MATLAB图注意力网络GAT多标签图分类预测可视化
Python用CEEMDAN-LSTM-VMD金融股价数据预测及SVR、AR、HAR对比可视化
Python注意力机制Attention下CNN-LSTM-ARIMA混合模型预测中国银行股票价格|附数据代码
