箱形图 非常有用，因为它们不仅指示中间值，而且还显示了第一四分位数和第三四分位数的测量结果变化。
但是，也有一些图提供了一些附加信息。在这里，我们将仔细研究箱形图的潜在替代方案：蜂群图和小提琴图。
可下载资源
蜂群图
原则上，蜂群图类似于一维散点图，因为它将单个测量结果显示为点。但是，不同之处在于，蜂群图采用了一种逻辑，以确保所绘制的点彼此靠近且不会重叠。
那么，什么时候应该使用蜂群图？由于蜂群图中的点不应重叠，因此此类图仅适用于相对少量的测量。如果测量结果显示不同的组，则它们也适用，因为各个点可以相应地着色。
在R中使用蜂群图
我们将使用 warpbreaks数据集 来举例说明绘图的用法。
# 选择 1: 按颜色分组
beeswarm(breaks ~ wool + tension, data = warpbreaks,
main = "Beeswarm of breaks versus wool and tension",
col = rep(c("red", "blue"), 3))
# 选项2：为单个点着色
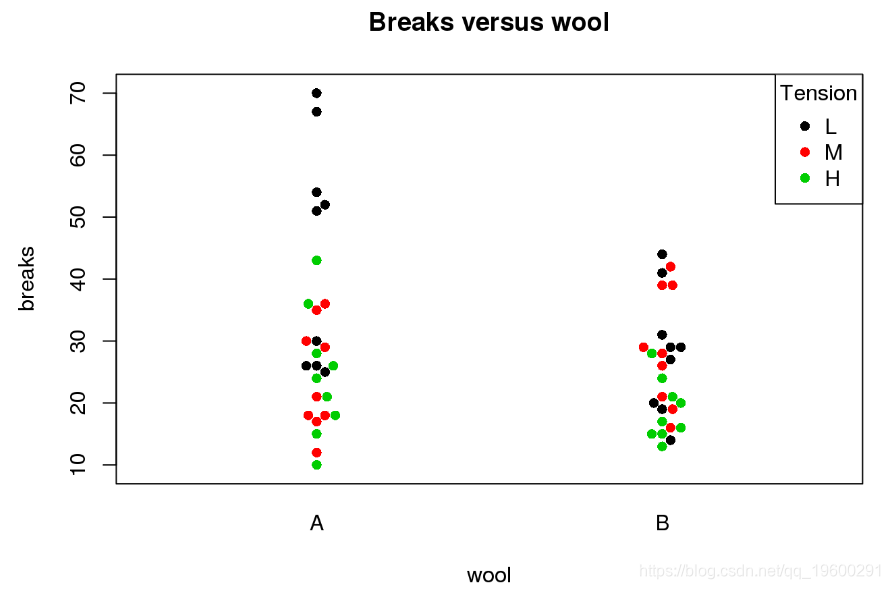
蜂群图也可以通过以下方式与箱形图组合：
beeswarm(breaks ~ wool, data = warpbreaks,
main = "Beeswarm of breaks versus wool", add = TRUE,
pwcol = as.numeric(tension), pch = 16)
小提琴图
小提琴图的想法是将箱形图和密度图结合起来。由于该图依赖于密度估计，因此只有在有足够数量的数据可用于获得可靠估计时，该图才有意义。否则，估计的密度可能表示数据中实际上没有的趋势。
在R中创建小提琴图
为了演示小提琴图与箱形图的不同之处，请比较以下两种表示形式：
grid.arrange(p.violin, p.box, ncol = 2)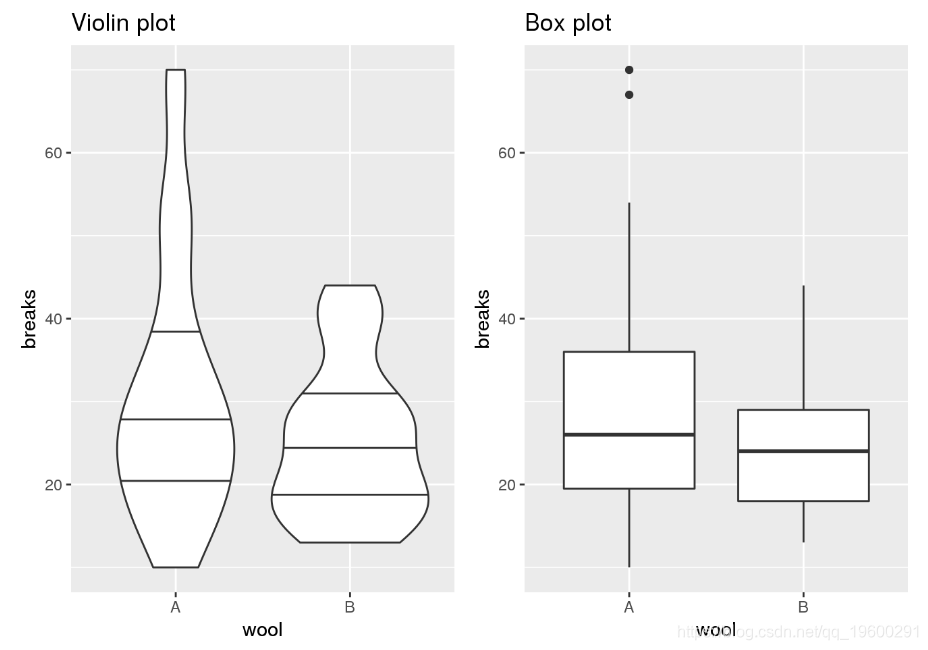
在这种情况下，我们看到了小提琴情节的限制，对于小样本量 。 另一方面，箱形图显示，实际上只有两个测量值大于60。
【视频】因子分析简介及R语言应用实例：对地区经济研究分析重庆市经济指标
R语言宏观经济学：IS-LM曲线可视化货币市场均衡
R语言代做编程辅导和解答GLM Coursework
R语言分析上海空气质量数据：kmean聚类、层次聚类、时间序列分析：arima模型、指数平滑法
