在数据科学的广阔领域中,处理多变量数据是一个常见且复杂的任务。当我们面对多个变量(如(a)和(b))时,常常需要以参数化的方式描述它们的联合分布(P(a, b))。
理想情况下,这种联合分布可能具有某种 “简单” 的性质,例如变量之间的统计独立性,此时(P(a, b) = P(a) P(b)),我们只需分别找到(P(a))和(P(b))的合适参数描述即可。
然而,在处理真实数据集时,(P(a, b))通常具有复杂的相关结构,使得上述简单方法不再适用,因此需要寻找替代方法。
本专题合集聚焦于运用Copula方法来解决这一问题。Copula允许我们通过简单的多元分布(如多元高斯分布)、两个边缘分布以及一些变换,来描述具有复杂相关结构的分布(P(a, b))。
本专题详细介绍了如何使用贝叶斯方法推断Copula的参数,从而实现对多变量联合分布的准确建模。专题中通过一系列的步骤展示了整个过程。首先,介绍了数据生成过程,从定义高斯Copula的属性开始,通过从多元正态分布中抽样,经过一系列变换,将数据从多元正态空间转换到观察空间。然后,阐述了Copula推断过程,即从观察空间反向转换到多元正态空间,这一过程是PyMC模型中使用的关键方法。
接着,展示了使用PyMC进行Copula和边缘估计的模型。在实验中发现,同时估计边缘分布的参数和Copula的协方差参数的模型不稳定,因此采用了两步法:先估计边缘分布的参数,再利用这些点估计值来估计Copula的协方差参数。
最后,通过可视化检查,将推断结果(红色)与原始观察数据(黑色)进行比较,验证了方法的有效性。
本专题合集已分享在交流社群,阅读原文进群和500+行业人士共同交流和成长。希望本专题能够为数据科学领域的研究者和从业者提供有价值的参考,帮助大家更好地处理多变量数据中的复杂相关结构问题。
数据生成过程
在深入研究推断之前,我们先详细阐述数据生成的步骤。
AI提示词:生成用于展示高斯Copula数据生成过程的Python代码,定义高斯Copula属性,从多元正态分布抽样并进行变换到观察空间,使用numpy、scipy.stats、seaborn等库,变量名可自定义。
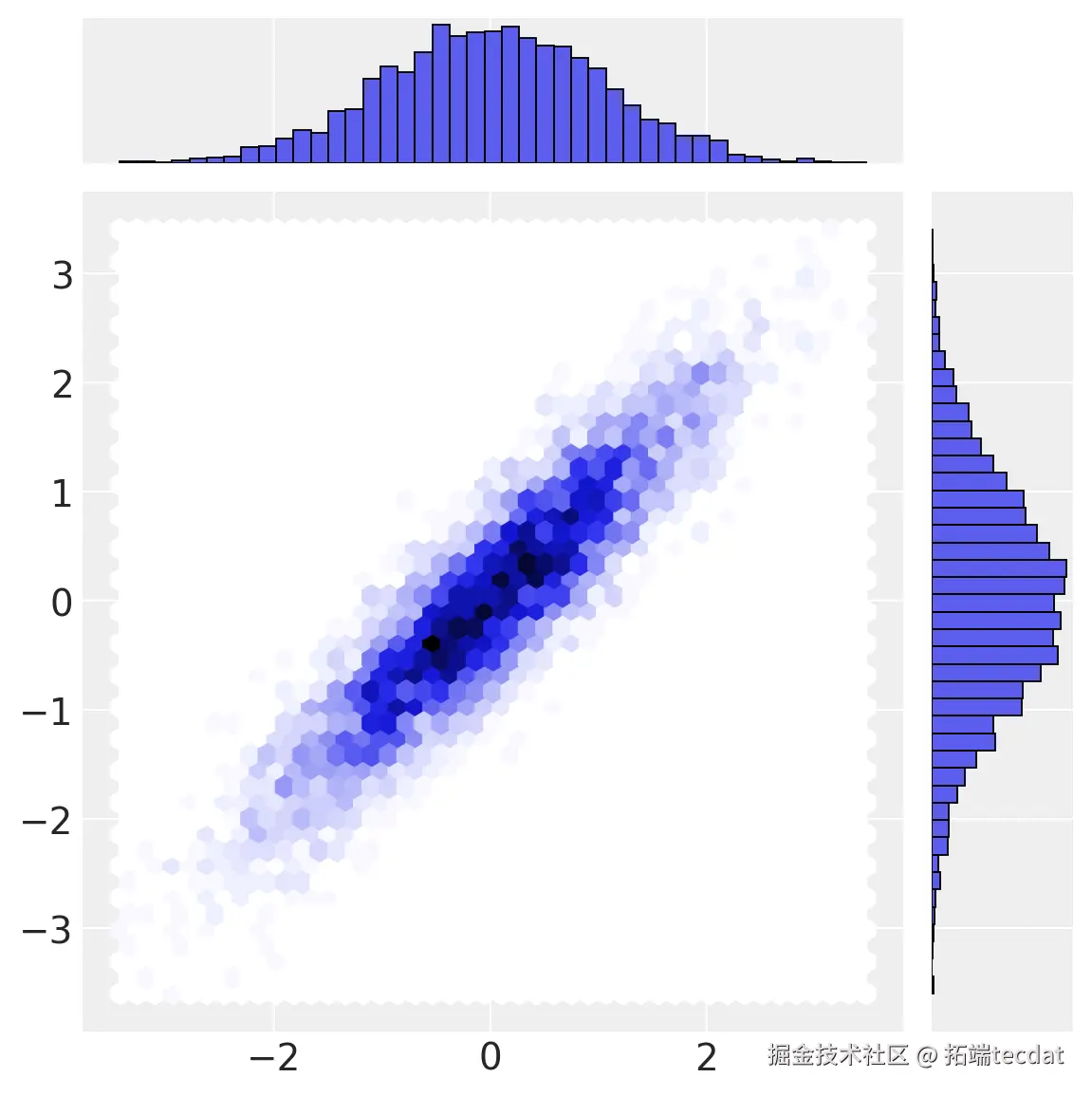
import numpy as np import scipy.stats as stats import seaborn as sns import matplotlib.pyplot as plt # 定义我们的Copula属性 b_scale = 2 theta = {"a_dist": stts.norm(), "ist": ss.expon(cale= / b_scale), "rho": 0.9} # 设定样本数量并从多元正态分布中抽样 n_samples = 5 # 绘制散点图 sns.joitplt(x=_nor, y=b_上述代码首先定义了高斯Copula的属性,包括边缘分布和相关系数。然后,从具有特定均值和协方差的多元正态分布中抽取一定数量的样本。接下来,进行第一次变换,将数据从多元正态空间转换为均匀空间,此时边缘分布变为均匀分布,但多元正态空间中的相关结构仍保留在联合密度中。
AI提示词:在上述代码基础上,添加将数据从多元正态空间转换为均匀空间的代码,并绘制转换后数据的散点图。
# 使边缘分布变为均匀分布
a_unif = stats.norm(loc=0, scale=1).cdf(a_norm)作者

Kaizong Ye
可下载资源
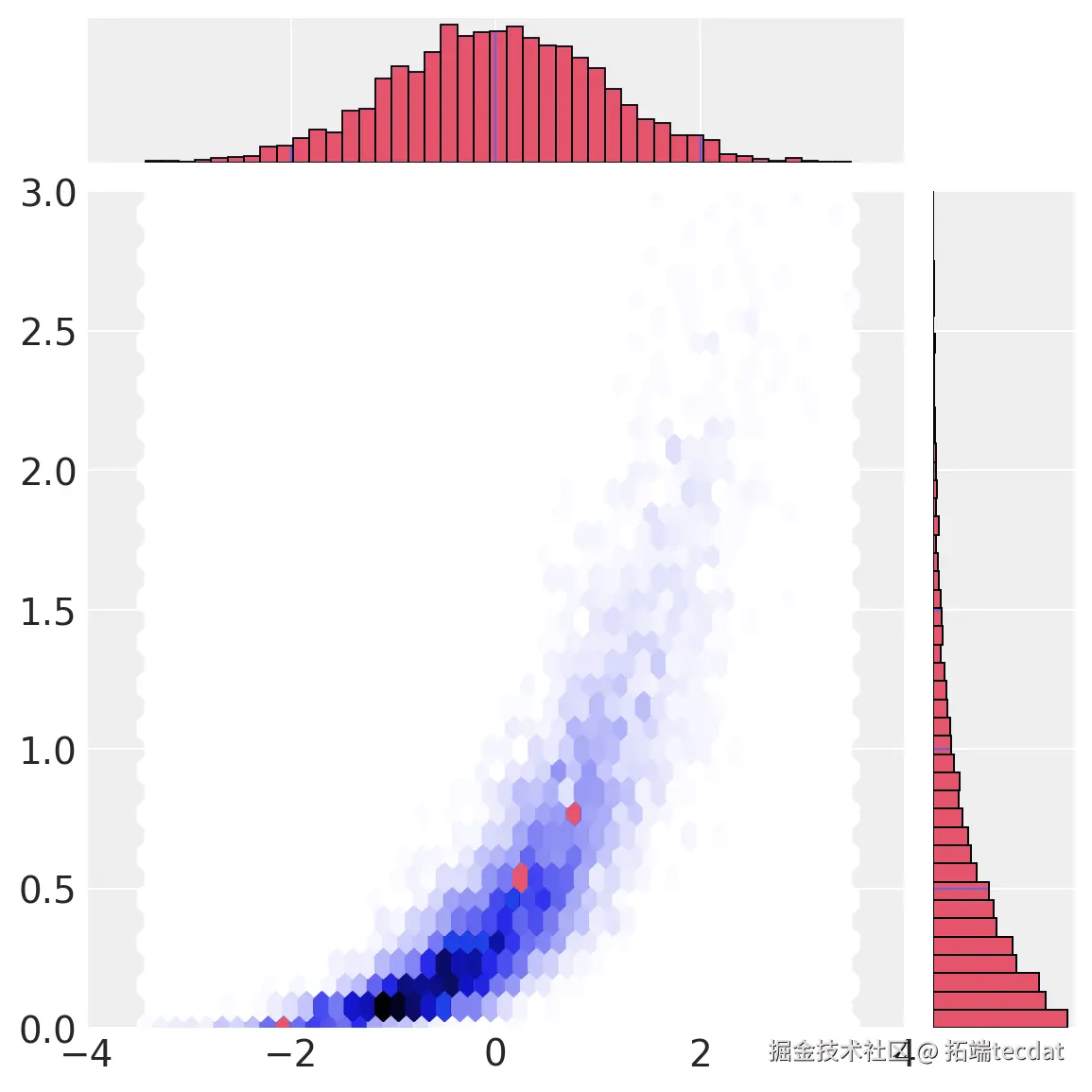
最后,进行最终变换,通过边缘分布的逆累积分布函数将数据从均匀空间转换到观察空间。
AI提示词:在上述代码基础上,添加将数据从均匀空间转换为观察空间的代码,并绘制转换后数据的散点图,设置合适的x轴和y轴范围。

想了解更多关于模型定制、咨询辅导的信息?
# 转换到观察空间
a = theta["a_dist"].ppf(a_unif)
Copula推断过程
为了理解所采用的方法,我们需要逐步研究从观察空间到多元正态空间的逆过程。
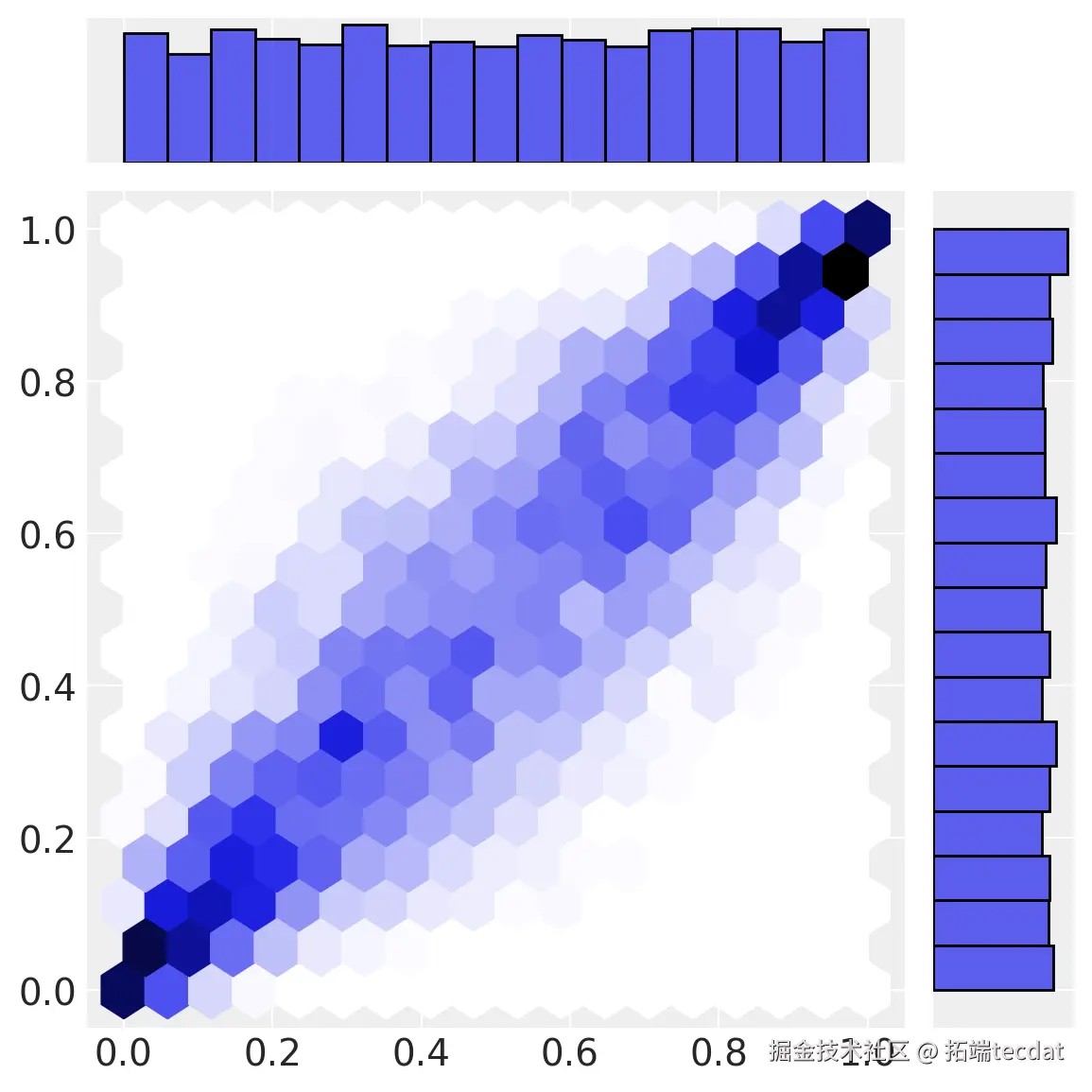
AI提示词:编写Python代码实现从观察空间到均匀空间的转换,并绘制散点图,使用已定义的变量a和b以及相关分布函数。
# 观察空间 -> 均匀空间
a1 = theta["a_dist"].cdf(a)
AI提示词:在上述代码基础上,添加从均匀空间到多元正态空间的转换代码,并绘制散点图。
# 均匀空间 -> 多元正态空间
a2 = stats.norm(loc=0, scale=1).ppf(a1)
PyMC模型用于Copula和边缘估计
我们的目标是在多元正态空间中对参数进行推断,同时利用观察空间中的数据来约束合理的参数值。在实验中,我们尝试了同时估计边缘分布参数和Copula协方差参数的模型,但发现其不稳定。因此,采用了更稳健的两步法:
- 估计边缘分布的参数;
- 使用第一步中边缘分布参数的点估计值来估计Copula的协方差参数。
AI提示词:编写使用PyMC估计边缘分布参数的Python代码,定义模型,设置变量和分布,使用给定的观察数据a和b,绘制模型图。
随时关注您喜欢的主题
import pymc as pm import arviz as az with pm.Model(coords=coords) as marginal_model: """ 假设观察数据在变量`a`和`b`中 """ # 边缘估计 a_mu = pm.Normal("a_mu", mu=0, sigma=1) a_sigma = pm.Exponential("a_sigma", lam=0.5)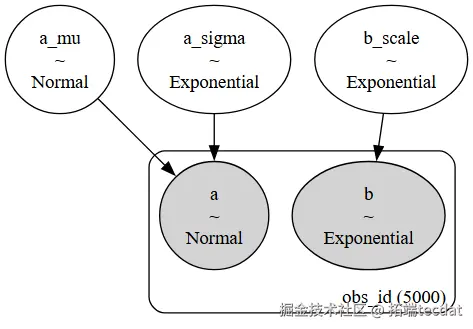
AI提示词:在上述代码基础上,添加从模型中采样并绘制后验分布的代码,设置合适的随机种子和变量名。
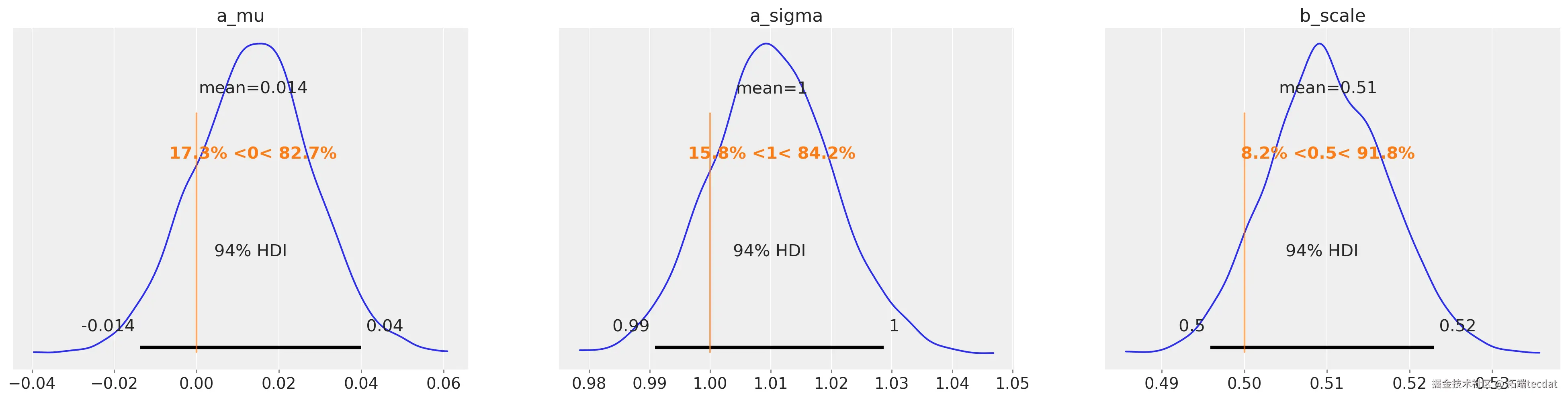
接下来,在Copula模型中,我们为协方差参数设置先验分布,后验分布由多元正态空间中的数据约束。为了实现这一点,需要将观察空间中的观测值([a, b])转换为多元正态空间,并存储在data中。
AI提示词:编写将观察数据从观察空间转换到多元正态空间的函数,使用边缘分布参数的点估计值,返回转换后的数据和相关参数,使用PyMC和Theano库。
def transom_daa(maginalidata):
# 点估计
a_mu = marginal_idata.posteror["a_m].mean().item()
# 从观察空间 -> 均匀空间的转换
__a = pt.exp(pm.locd(pm.Nomal.dt(m=a_mu,sima=a_sigma), a))
# 均匀空间 -> 多元正态空间
_a = pm.math.pbit__a)
# 连接成Nx2矩阵
data = pt.ath.ta([_a _b], ax=1).evalAI提示词:编写定义Copula模型的Python代码,设置协方差的先验分布,定义似然函数,使用转换后的数据,绘制模型图。
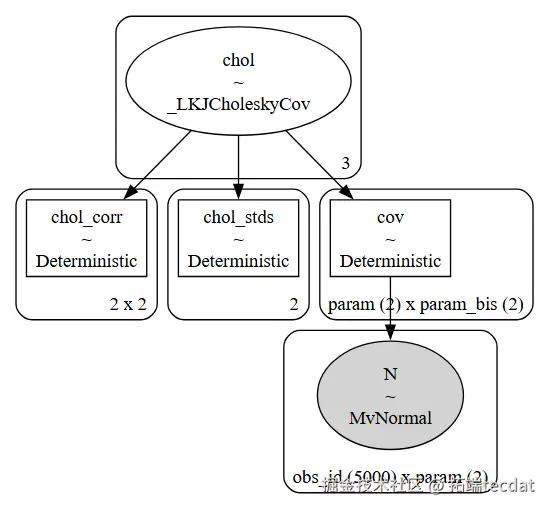
with pm.Model(coords=coords) as copula_model:
# 多元正态协方差的先验
chol, corr, stds = pm.LKhlekyCov(
"chol",
n=2,
# 似然函数
pm.MvNormal("N", mu=0.0, cov=cov, observed
AI提示词:在上述代码基础上,添加从Copula模型中采样并绘制后验分布的代码,设置合适的随机种子、调整步数和核心数,设置参考值。
with cpula_odel:
copula_iaa = pm.smle(ndom_ed=nrndom.dfaul_rg(43), une2000
通过以上步骤,我们成功恢复了用于生成样本数据的多元正态Copula的协方差矩阵。
与真实数据比较推断结果
最后,我们通过可视化检查来判断推断结果(红色)是否与原始观察数据(黑色)相符。
AI提示词:编写Python代码提取Copula模型后验数据中的协方差估计值,生成新的((a, b))样本,进行空间转换并绘制原始数据和推断结果的对比图,使用arviz库的plot_pair函数。
# 数据处理以提取有用形状的协方差估计值
d = {k: v.values.reshape((-1, *v.shape[2:])) for k, v in copula_idata.posterior[["cov"]].items()}
# 生成(a, b)样本
ab = np.vstack([stats.multivariate_normal([0, 0], cov).rvs() for cov in d["cov"]])
# 转换到均匀空间
uniform_a = stats.norm().cdf(ab[:, 0])
# 转换到观察空间
# 绘制原始数据(黑色)
ax = az.plot_pair(
{"a": a, "b": b},
marginals=True,
kind="kde",
# 绘制推断结果(红色)
axs = az.plot_pair(
{"a": ppc_a, "b": ppc_b},
从图中可以直观地看到,红色的推断结果与黑色的原始观察数据在分布特征上具有较高的相似性,这表明我们所采用的基于贝叶斯方法的Copula参数推断过程是有效的。通过这种方式,我们能够较为准确地从观察数据中反推回多元正态空间中的参数,进而对复杂的联合分布进行合理建模和分析。
总结与展望
在本次专题合集中,我们从处理多变量联合分布时面临的复杂相关结构问题出发,引入了Copula这一有力工具,并详细阐述了如何借助贝叶斯方法利用PyMC进行Copula参数推断。
通过逐步解析数据生成过程,从多元正态空间到观察空间的变换,以及逆过程的Copula推断,我们清晰地展示了整个方法的逻辑脉络。在PyMC模型构建环节,我们针对同时估计边缘分布和Copula协方差参数的模型不稳定性问题,创新性地采用了两步法进行估计,有效提升了模型的稳健性。这种创新的两步法估计策略,相较于传统方法,在处理实际复杂数据集时具有更高的可靠性和准确性。
在与真实数据的对比验证中,我们成功地通过推断结果还原出与原始观察数据分布特征高度契合的模型,进一步证明了方法的有效性。
展望未来,随着数据规模和复杂性的不断增加,我们可以探索将该方法应用于更高维度的多变量联合分布分析。同时,进一步优化模型参数估计过程,提高计算效率,也是未来研究的重要方向之一。此外,结合其他先进的数据处理技术,如深度学习等,拓展Copula方法在更广泛领域的应用,将为数据科学研究带来新的机遇和挑战。我们期待通过不断的研究和实践,为解决实际问题提供更加精准和高效的数据分析方法。
每日分享最新报告和数据资料至会员群
关于会员群
- 会员群主要以数据研究、报告分享、数据工具讨论为主;
- 加入后免费阅读、下载相关数据内容,并同步海内外优质数据文档;
- 老用户可九折续费。
- 提供报告PDF代找服务
非常感谢您阅读本文,如需帮助请联系我们!


 Python+AI提示词用LSTM和注意力机制的苹果公司股票价格预测
Python+AI提示词用LSTM和注意力机制的苹果公司股票价格预测 Python+AI提示词贝叶斯项目反应IRT理论Rasch分析篮球比赛官方数据:球员能力与位置层级结构研究
Python+AI提示词贝叶斯项目反应IRT理论Rasch分析篮球比赛官方数据:球员能力与位置层级结构研究 Python+AI提示词比特币数据预测:Logistic逻辑回归、SVC及XGB特征工程优化实践
Python+AI提示词比特币数据预测:Logistic逻辑回归、SVC及XGB特征工程优化实践 Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析
Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析
