本文描述了帮助客户使用马尔可夫链蒙特卡洛(MCMC)方法通过贝叶斯方法估计基本的单变量随机波动模型,就像Kim等人(1998年)所做的那样。
定义模型以及从条件后验中抽取样本的函数的代码也在Python脚本中提供。
%matplotlib inline
from __future__ import division
......
from src import sv
来自Kim等人(1998年)的经典单变量随机波动性模型,在此之后简称KSC,如下所示:
可下载资源
这里,yt代表某个资产的修正后平均收益,ht为对数波动率
示例
我们将对1981年10月1日至1985年6月28日期间的英镑/美元汇率进行建模。
视频
随机波动率SV模型原理和Python对标普SP500股票指数时间序列波动性预测
视频
马尔可夫链蒙特卡罗方法MCMC原理与R语言实现
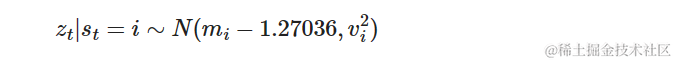
其中 st 是一个指示随机变量,定义为 P(st=i)=qi, i=1,…,K (K 是混合成分数目)。定义了 (qi,mi,v2i) 表示组成高斯分布的值如下所示。
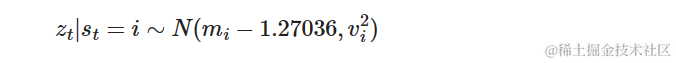
# q_i, m_i, v_i^2
ksc_aras = np.array([......
)
在给定 stTt=1 的条件下,每个时间段的观测方程是由一个高斯噪声项定义的。
通过设置 K=7 是对 logε2t 进行很好近似的方法,Omori et al. (2007) 将其扩展到 K=10。
class TLDT(sm.t......
Model):
"""
时变局部线性确定性趋势
......
# 转换为对数平方,带有偏移量
endog = n.logenog**2+ offset
# 初始化基本模型
super(TVLLDT, self)._......
tationary')
# 设置观测方程的时变数组
self['o......
.nobs))
# 设置状态空间矩阵的固定分量
self['d......
0] = 1
def update......
7036, v_i^2)
self['o......
rams[1]
self['state_cov', 0, 0] = params[2]
ϕ 的先验分布
定义 ϕ∗=(ϕ+1)/2,我们对 ϕ∗ 指定一个先验分布:
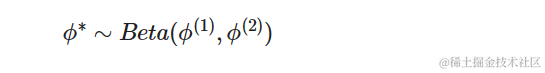
正如在 KSC 中讨论的那样,该先验分布在 (−1,1) 上支持随机波动性过程的平稳性。
设置 ϕ(1)=20 和 ϕ(2)=1.5 意味着 E[ϕ]=0.86。
最后:
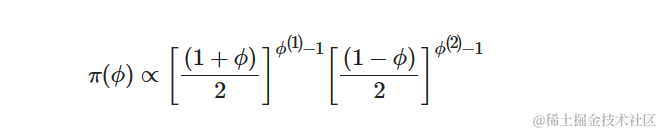
随时关注您喜欢的主题
我们可以应用 Metropolis 步骤:从 N(ϕ^,Vθ) 中生成一个提议值 ϕ∗
def g(phi, ......
# 先验分布对非平稳过程给予零权重
if np.abs(phi) >= 1:
ret......
2) / 2 * sigma2
tmp2 = 0.5 * np.log(1 - phi**2)
return n......
V_phi = sigma2 / tmp2
proposal ......
om.uniform() else phi
采样μ̂
条件后验分布为:
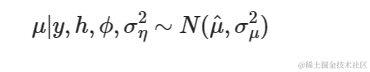
def draw_pos......
* (1 - phi)**2 + ......
)
return norm.r......
2_mu**0.5)
采样htTt=1̂
在混合指示符(用于生成时变观测方程矩阵)和参数条件下,可以通过通常的模拟平滑器对状态进行采样。
采样stTt=1̂
每个指示变量st只能取有限个离散值(因为它是一个指示变量,表示时间t时哪个混合分布处于活动状态)。KSC表明,可以从以下概率质量函数独立地采样混合指示符:
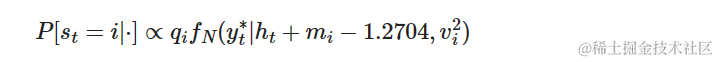
其中fN(y∗t∣a,b)表示均值为a,方差为b的高斯随机变量在y∗t处的概率密度。
def (mod states):
resid = od.nog[:, 0] - states[0]
# 构建均值 (nobs x 7), 方差 (7,), 先验概率 (7,)
means = ks_aram......
0]
# 调整维度以便广播计算
resid = np.repe......
[None, :], mod.nobs,
axis=0)
# 计算对数似然 (nobs x 7)
loglikelihoods = -0.5 * ((resi......
* variances))
# 得到(与后验(对数))成比例的值 (nobs x 7)
posterior_kernel = log......
ilities)
# 归一化得到实际后验概率
tmp = logsumxp(psterir_kernl,axis=1)
posterior_probabilitie......
d, states)
# 从后验中抽取样本
varaes = np.radom.niorm(ize=od.obs)
......
sample = np.argmax(tmp, axis=1)
return sample
MCMC
下面我们进行10,000次迭代以从后验中进行抽样。在下面展示结果时,我们将舍弃前5,000次迭代作为燃烧期,并且在剩下的5,000次迭代中,我们只保存每十次迭代的结果。然后从剩下的500次迭代中计算结果。
# 设置模型和模拟平滑器
md = TVLLT(eog)
mo.(0, sothr_stateTrue)
sim = md.siutin_sother()
# 模拟参数
nitertons = 10000
brn = 5000
tin = 10
# 存储轨迹
trae_sooted = np.eros((_iteations+ 1 mod.nobs))......
trce_sim2 = np.ers((n_iteations + 1, 1))
# 初始值 (p. 367)
trce_miing[0] = 0
[0] = 0.95
trace_sigma2[0] = 0.5
# 迭代
for s in range(1, n_teations + 1):
# 更新模型参数
mod.updat_ming(tace_mixing[s-1])......
# 模拟平滑
sim.smuate()......
# 抽取混合指标
trac_miing[s] = drawmixngmod states)
# 抽取参数
tra_phi[s] = (mod, sates, trace_phi[s-1], trace_mu[s-1], trace_sigma2[s-1])......
结果
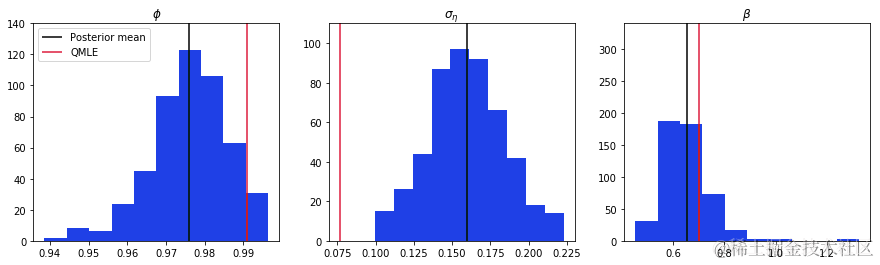
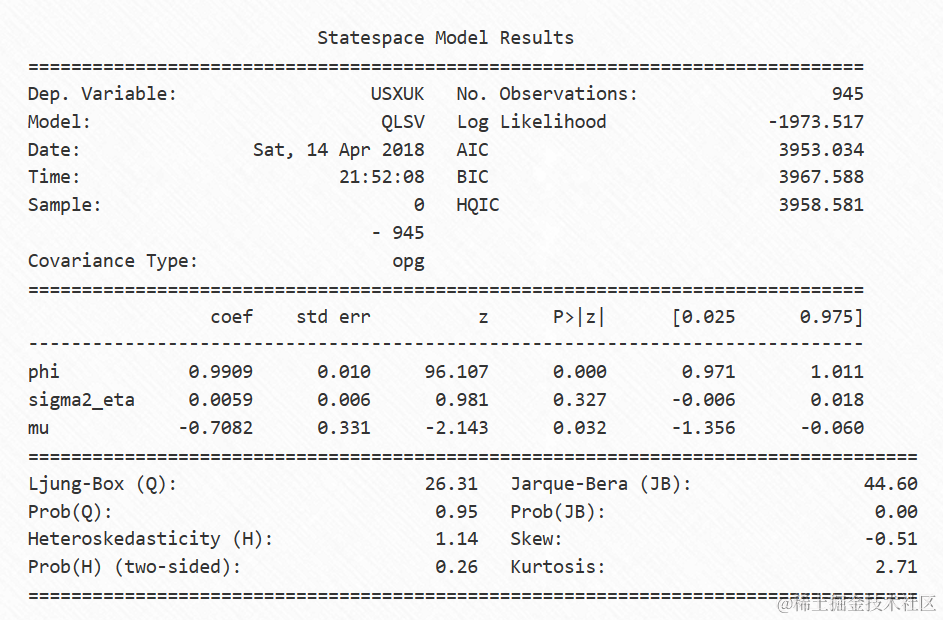
下面我们给出参数的后验均值。我们还展示了相应的QMLE估计值。这些估计值与 ϕ 和 β 的后验均值相似,但是对于 ση² 的QMLE估计值约为贝叶斯方法的一半,可能表明准拟然方法的一个缺点。
# 参数的后验均值
menphi = n.men(trae_hi[burn:thin])......
print(' beta = %.5f' % npexp(rs_LSVparams[2] / 2))

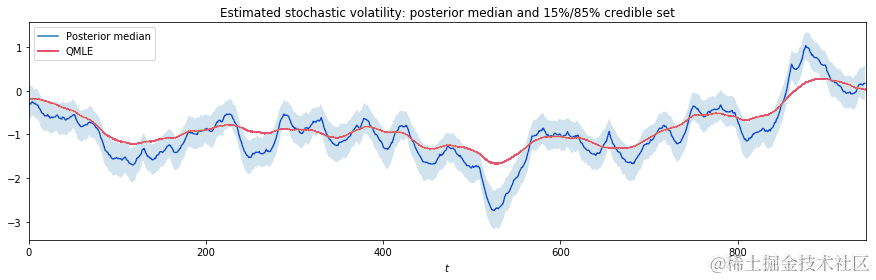
由于参数ση²控制潜在随机波动率过程的方差,低估将抑制样本中波动率过程的变化。如下图所示
fig, ax = plt.subplots(f......
ax.legend();
最后,我们可能对参数的完全条件后验分布感兴趣。以下是这些分布,以及后验均值和QMLE估计值。
fig, axes = plt.subplots(1, 3, ......
axes[0].set(title=r'$\phi$', ylim=ylim)
axes[0].legend(loc='upper left')
......
axes[2].set(title=r'$\beta$', ylim=ylim);
可下载资源
关于作者
Kaizong Ye是拓端研究室(TRL)的研究员。在此对他对本文所作的贡献表示诚挚感谢,他在上海财经大学完成了统计学专业的硕士学位,专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文,如需帮助请联系我们!

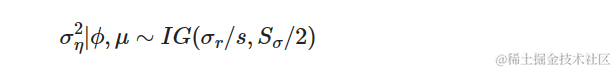
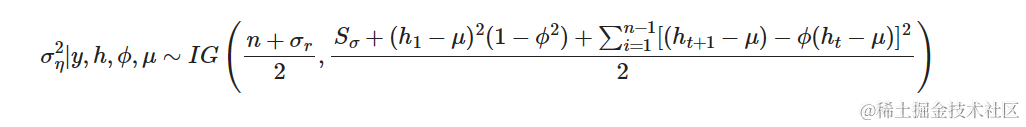
 R语言Stan贝叶斯回归置信区间后验分布可视化模型检验
R语言Stan贝叶斯回归置信区间后验分布可视化模型检验 R语言贝叶斯INLA空间自相关、混合效应、季节空间模型、SPDE、时空分析野生动物数据可视化
R语言贝叶斯INLA空间自相关、混合效应、季节空间模型、SPDE、时空分析野生动物数据可视化 Python贷款违约预测:Logistic、Xgboost、Lightgbm、贝叶斯调参/GridSearchCV调参
Python贷款违约预测:Logistic、Xgboost、Lightgbm、贝叶斯调参/GridSearchCV调参 R语言汇率、股价指数与GARCH模型分析:格兰杰因果检验、脉冲响应与预测可视化
R语言汇率、股价指数与GARCH模型分析:格兰杰因果检验、脉冲响应与预测可视化


