最近我们被客户要求撰写关于马可夫转换模型的研究报告。本文提供了一个在统计模型中使用马可夫转换模型的例子，来复现Kim和Nelson（1999）中提出的一些结果。
它应用了Hamilton（1989）的滤波器和Kim（1994）的平滑器。
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
from pandas_datareader.data import DataReader
from datetime import datetime
DataReader(start=datetime(1947, 1, 1), end=datetime(2013, 4, 1))1906年，Andrey Andreyevich Markov为了描述随机过程首次提出了马尔科夫链，并应用在俄语字符序列的计算中。在随后的半个世纪中，该概念深刻影响了数学，统计，计算机，物理学，生物学，语言学等各个领域，并引申发展出了马尔可夫毯，马尔可夫模型，马尔可夫随机场等多种重要概念。
大名鼎鼎的MCMC本质上是将马尔可夫链用于对蒙特卡洛方法的积分过程中，由梅特罗波利斯于1953年在洛斯阿拉莫斯国家实验室提出。那时美国洛斯阿拉莫斯是当时少数几个拥有大规模计算机的城市，梅特罗波利斯则利用这种计算优势，在蒙特卡洛方法的基础上引入马尔可夫链，用于模拟某种液体在气化之后的平衡状态。1984年Stuart和Donald Geman兄弟对吉布斯采样进行了描述，形成了我们今天所熟悉的版本，而吉布斯采样就是一种简单且广泛适用的马尔可夫链蒙特卡洛（MCMC）算法。
时间再倒回一点，1957年，RICHARD BELLMAN提出了马尔可夫决策过程，这是基于马尔可夫过程理论的随机动态系统的最优决策过程，而马尔可夫过程的原始模型就是马尔科夫链。1980年，《Markov random fields and their applications》出版，详细描述了马尔可夫随机场的理论和应用，马尔可夫随机场实际上是马尔可夫过程的一个多维版本。1988年，Judea Pearl在其著作Probabilistic reasoning in intelligent systems: networks of plausible inference中提出了马尔可夫毯的概念。1991年，Lovejoy 研究了部分可观测马尔可夫决策过程（POMDP）。1995年D. P. Bertsekas 和 J. N. Tsitsiklis讨论了一类用于不确定条件下的控制和顺序决策的动态规划方法。 这些方法具有处理长期以来由于状态空间较大或缺乏准确模型而难以处理的问题的潜力，他们将规划所基于的环境表述为马尔可夫决策过程，这即是目前深度学习领域流行的强化学习的雏形。
1966年起，Leonard E. Baum等学者在一系列研究中提出了隐马尔可夫模型（Hidden Markov Model，HMM），它用来描述一个含有隐含未知参数的马尔可夫过程。1975年，Baker 将 HMM 用于语音识别，从那以后，HMM成为了大多数现代自动语音识别系统的基础。20世纪80年代起，HMM 也开始用于分析生物序列（DNA）。
在经济金融领域，James D. Hamilton 1989年机应用了制转换模型，其中马尔科夫链用来对高GDP增长速度时期与低GDP增长速度时期（换言之，经济扩张与紧缩）的转换进行建模。S.Brin和L.Page提出的谷歌所使用的网页排序算法（PageRank）（1998年），也是由马尔可夫链定义的。如果N是已知的网页数量，一个页面i有k_i个链接到这个页面，那么它到链接页面的转换概率为\alpha/k_i+(1-\alpha)/N，到未链接页面的概率为(1-\alpha)/N， 参数\alpha的取值大约为0.85。
在深度学习领域，Yoshua Bengio 等研究者于2017年提出了 GibbsNet，旨在通过匹配模型期望的联合分布和数据驱动的联合分布直接定义和学习转换算子（transition operator），然后使用转换算子训练图模型，成功将马尔科夫链与神经网络结合起来。同年，Jiaming Song, Shengjia Zhao和Stefano Ermon研究了生成对抗的训练方法来对马尔可夫链（Markov chain）的转移算子（transition operator）进行学习，目的是将其静态分布（stationary distribution）和目标数据分布相匹配。他们提出了一种新型的训练流程，以避免从静态分布中直接采样，但是仍然有能力逐渐达到目标分布。此模型可以从随机噪声开始，是无似然性的，并且能够在单步运行期间生成多个不同的样本。初步试验结果显示，当它临近其静态时，马尔可夫链可以生成高质量样本，即使是对于传统生成对抗网络相关理念中的较小结构亦是如此。
主要事件
| 年份 | 事件 | 相关论文/Reference |
| 1906 | Andrey Andreyevich Markov 引入了马尔可夫链的概念 | Markov, A. A. (1906). Rasprostranenie zakona bol’shih chisel na velichiny, zavisyaschie drug ot druga. Izvestiya Fiziko-matematicheskogo obschestva pri Kazanskom universitete, 15(135-156), 18. |
| 1953 | 梅特罗波利斯将蒙特卡洛方法引入马尔可夫链 | Metropolis, Nicholas; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (1953). “Equation of State Calculations by Fast Computing Machines”. |
| 1957 | 马尔可夫决策过程被提出 | Bellman, R. (1957). A Markovian decision process. Journal of Mathematics and Mechanics, 679-684. |
| 1966 | Leonard E. Baum等学者在一系列研究中提出了隐马尔可夫模型（Hidden Markov Model，HMM） | Baum, L. E.; Petrie, T. (1966).Statistical Inference for Probabilistic Functions of Finite State Markov Chains. The Annals of Mathematical Statistics. 37 (6): 1554–1563. |
| 1975 | Baker 将 HMM 用于语音识别 | Baker, J.(1975). The DRAGON system—An overview.IEEE Transactions on Acoustics, Speech, and Signal Processing. 23: 24–29. |
| 1980 | 《Markov random fields and their applications》出版，详细描述了马尔可夫随机场的理论和应用 | Kindermann, R., & Snell, J. L. (1980). Markov random fields and their applications (Vol. 1). American Mathematical Society. |
| 1984 | Stuart和Donald Geman兄弟描述了Gibbs抽样算法 | Geman, S.; Geman, D.(1984). Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images.IEEE Transactions on Pattern Analysis and Machine Intelligence. 6 (6): 721–741. |
| 1988 | Judea Pearl提出马尔可夫毯的概念 | Pearl, J. (2014). *Probabilistic reasoning in intelligent systems: networks of plausible inference*. Morgan Kaufmann. |
| 1989 | James D. Hamilton 1989年机应用了制转换模型 | Hamilton, J. (1989). A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica. 57 (2): 357–84. |
| 20世纪80年代 | HMM 开始用于分析生物序列（DNA） | Bishop, M. and Thompson, E. (1986). Maximum Likelihood Alignment of DNA Sequences.Journal of Molecular Biology. 190 (2): 159–165. |
| 1991 | Lovejoy 研究了部分可观测马尔可夫决策过程（POMDP） | Lovejoy, W. S. (1991).A survey of algorithmic methods for partially observed Markov decision processes.Annals of Operations Research. 28(1):47–65. |
| 1995 | D. P. Bertsekas 和 J. N. Tsitsiklis讨论了一类用于不确定条件下的控制和顺序决策的动态规划方法 | Bertsekas D. P. and Tsitsiklis, J. N. (1995). Neuro-dynamic programming: an overview.Proceedings of 1995 34th IEEE Conference on Decision and Control. 1: 560-564. |
| 1998 | S.Brin和L.Page提出PageRank算法 | Page, L. (1998). The pagerank citation ranking : bringing order to the web. Stanford Digital Libraries Working Paper, 9(1), 1-14. |
| 2017 | Yoshua Bengio 等研究者提出了 GibbsNet | Lamb, A. et al. (2017).GibbsNet: Iterative Adversarial Inference for Deep Graphical Models.arXiv:1712.04120. |
| 2017 | Jiaming Song, Shengjia Zhao和Stefano Ermon研究了生成对抗的训练方法来对马尔可夫链（Markov chain）的转移算子（transition operator）进行学习 | Song, J.; Zhao, S.; Ermon, S. (2017).GENERATIVE ADVERSARIAL LEARNING OF MARKOV CHAINS. ICLR. |
Hamilton (1989) 马尔可夫转换模型（_Markov -switching_ _model_）
这是对Hamilton(1989)介绍马可夫转换模型（_Markov -switching_ _model_）的开创性论文的复现。该模型是一个4阶的自回归模型，其中过程的平均值在两个区制之间切换。可以这样写。
每个时期，区制都根据以下的转移概率矩阵进行转换。
其中 pij是从区制 i 转移到区制 j 的概率。
该模型类别是时间序列部分中的MarkovAutoregression。为了创建这个模型，我们必须指定k\_regimes=2的区制数量，以及order=4的自回归阶数。默认模型还包括转换自回归系数，所以在这里我们还需要指定switch\_ar=False。
创建后，模型通过极大似然估计进行拟合。使用期望最大化（EM）算法的若干步骤找到好的起始参数，并应用准牛顿（BFGS）算法来快速找到最大值。
\[2\]:
#获取数据
hamilton= pd.read('gndata').iloc\[1:\]
# 绘制数据
hamilton.plot()
# 拟合模型
Markovreg(hamilton)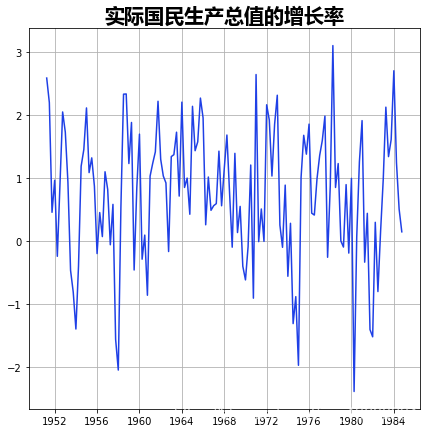
summary()
我们绘制了经过过滤和平滑处理的衰退概率。滤波指的是基于截至并包括时间tt（但不包括时间t+1,…,Tt+1,…,T）的数据对时间t的概率估计。平滑化是指使用样本中的所有数据对时间t的概率进行估计。
fig, axes = plt.subplots(2, figsize=(7,7))
ax = axes\[0\]
ax.plot(margl_prob\[0\])
ax = axes\[1\]
ax.plot(smoomarginal_pro\[0\])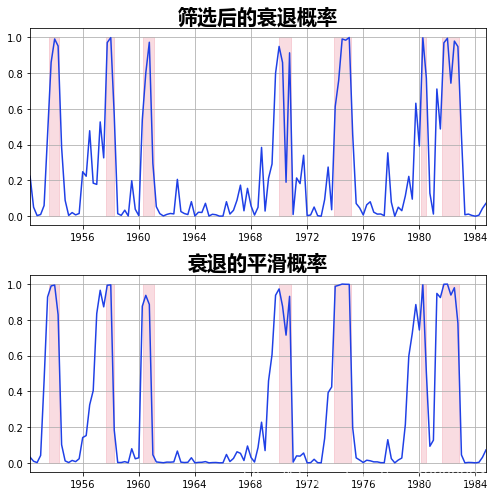
根据估计的转移矩阵，我们可以计算出衰退与扩张的预期持续时间。
print(expected_du)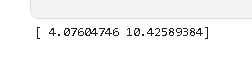
在这种情况下，预计经济衰退将持续约一年（4个季度），扩张约两年半。
随时关注您喜欢的主题
Kim, Nelson, and Startz (1998) 三状态方差转换模型。
这个模型展示了带有区制异方差（方差转换）和无平均效应的估计。
模型是:
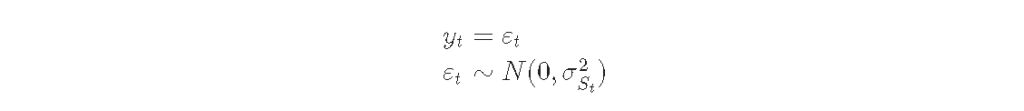
由于没有自回归成分，这个模型可以用MarkovRegression类来拟合。由于没有平均效应，我们指定趋势=’nc’。假设转换方差有三个区制，所以我们指定k\_regimes=3和switching\_variance=True（默认情况下，方差被假定为在不同区制下是相同的）。
raw = pd.read_table(ew ,engine='python')
# 绘制数据集
plot( figsize=(12, 3))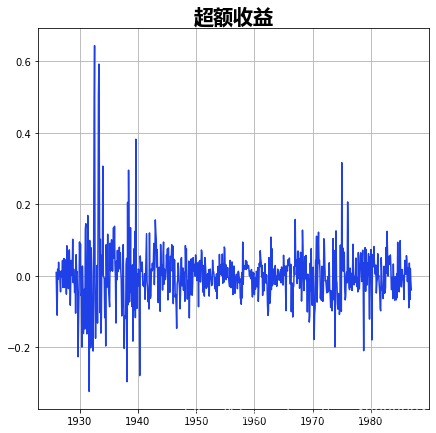
res_kns.summary()
下面我们绘制了处于每个区制中的概率；只有在少数时期，才有可能出现高_方差_区制。
fig, axes = plt.subplots(3, figsize=(10,7))
ax.plot(smoothed_proba\[0\])
ax.plot(smoothed_proba\[2\])
ax.plot(smoothed_proba\[3\])
Filardo (1994) 时变的转移概率
这个模型展示了用时变的转移概率进行估计。
在上述模型中，我们假设转移概率在不同时期是不变的。在这里，我们允许概率随着经济状况的变化而变化。否则，该模型就是Hamilton（1989）的马尔可夫自回归。
每个时期，区制现在都根据以下的时变转移概率矩阵进行转移。
其中 pij,tipij,t 是在 t 期间从区制 i 转移到区制 j 的概率，并定义为。
与其将转移概率作为最大似然法的一部分进行估计，不如估计回归系数βij。这些系数将转移概率与预先确定的或外生的变量xt-1向量联系起来。
\[9\]:# 用标准差进行标准化
data\['p'\]\['1960-01-01':\].std() / data\['dlip'\]\[:'1959-12-01'\].std()
# 绘制数据
data\['dlip'\].plot( )
data\['dmdlleading'\].plot( figsize=(13,3));
时变的转移概率是由exog_tvtp参数指定的。下面，我们规定对起始参数向量的20个随机扰动进行检查，并将最好的一个作为实际的起始参数。由于搜索的随机性，我们事先设置了随机数种子，以便结果复制。
这里我们展示了模型拟合的另一个特点–使用随机搜索的MLE起始参数。因为马尔科夫转换模型的特征往往是似然函数的许多局部最大值，执行初始优化步骤有助于找到最佳参数。
markovreg(data, k=2, order=4)
fit(search=20)
summary()
下面我们绘制了经济运行在低生产状态下的平滑概率，并再次将NBER的衰退情况纳入其中进行比较。
ax.plot(smoo\_marg\_prob\[0\])
利用时间变化的转移概率，我们可以看到低生产状态的预期持续时间如何随时间变化。
exp_dura\[0\].plot( figsize=(12,3));
在经济衰退期间，低生产状态的预期持续时间要比经济扩张时高得多。
可下载资源
关于作者
Kaizong Ye是拓端研究室（TRL）的研究员。在此对他对本文所作的贡献表示诚挚感谢，他在上海财经大学完成了统计学专业的硕士学位，专注人工智能领域。擅长Python.Matlab仿真、视觉处理、神经网络、数据分析。
本文借鉴了作者最近为《R语言数据分析挖掘必知必会 》课堂做的准备。
非常感谢您阅读本文，如需帮助请联系我们！
Python混合注意力机制-多变量-LSTM神经网络分析PM2.5、光伏电站、温度时间序列数据及RNN、ARIMAX、XGT、随机森林对比
MATLAB深度学习Transformer神经网络量化金融时间序列预测交易策略回测
【视频讲解】线性时间序列原理及混合ARIMA-LSTM神经网络模型预测股票收盘价研究实例
Python用Markov RNN马尔可夫递归神经网络建模序列数据t-SNE可视化研究
