流体力学界对过冷液体(supercooled liquid)的认知还不完善,我的项目利用Python的分子模拟,通过搭建一个binary hard disk system并对系统进行压缩模拟来验证Dynamic Facilitation Theory是否适用于我搭建的分子模型。
DF Theory包含以下理论推测
系统激发态密度与系统压力成log关系:
根据现代物理力学理论可知,力的本质其实就是宇宙中存在的四种相互作用,按照从强到弱的顺序,排在第一的是强相互作用,其可以使原子核里面的质子,中子稳定地存在。排在第二的是电磁相互作用,它贡献了化学键,分子间相互作用力,以及各种宏观世界的的力,比如表面张力,静电力,磁力等等。 排在第三的是弱相互作用,其也只有在原子核内有效,而且强度非常弱,虽然没有什么存在感,但是很重要,排在最后就是万有引力了,其强度极弱,对物质的性质没有可观察的影响,可以忽略不计了。
在这里主要介绍由电磁相互作用引起的分子间相互作用力,亦称分子间引力,是介导分子间相互作用的力,包括作用于原子和其他类型的相邻粒子(例如原子或离子)之间的吸引力或排斥力。分子间相互作用力(非键相互作用) 相对于分子内相互作用力(键相互作用) 来说是微弱的。例如,涉及原子之间共享电子对的共价键比相邻分子之间存在的力强得多。这两组力都是分子力学中常用力场的重要组成部分。
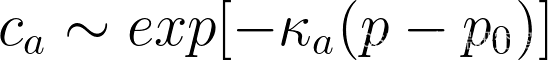
系统的弛豫时间和系统压力成如下关系:![]()
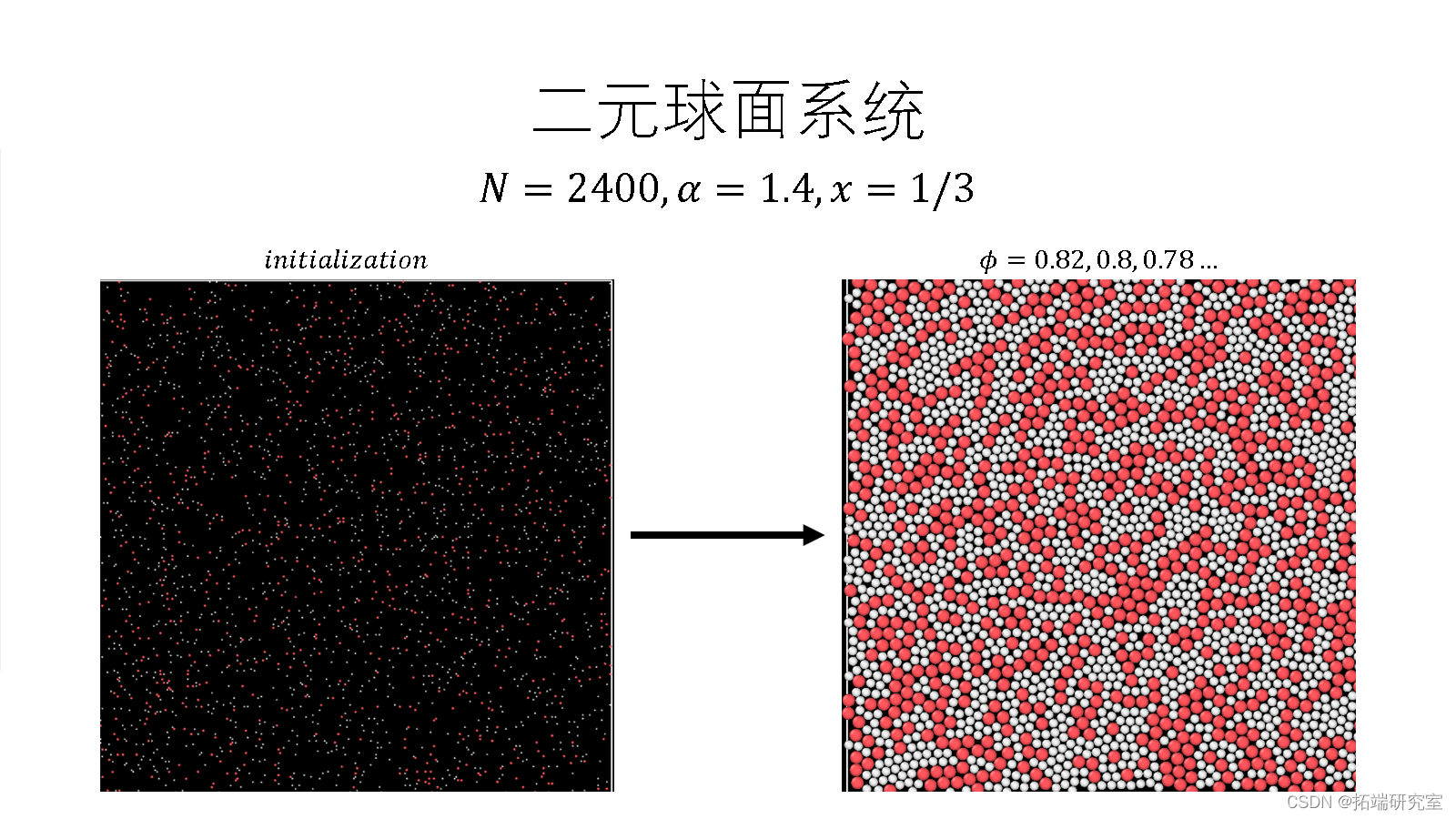
来源:项目PPT
我在Python内搭建如上binary hard disk模型, 并压缩系统至不同的密度来模拟过冷液体。压缩完成之后在此运行系统来模拟过冷液体常规布朗运动。在此期间,收集每一个粒子的实时坐标(x,y)并做如下计算:
- 辨别系统的激发态密度

- 验证系统激发态密度和系统压力是否成log关系
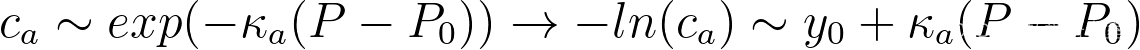
- 计算系统的弛豫时间(relaxation time)
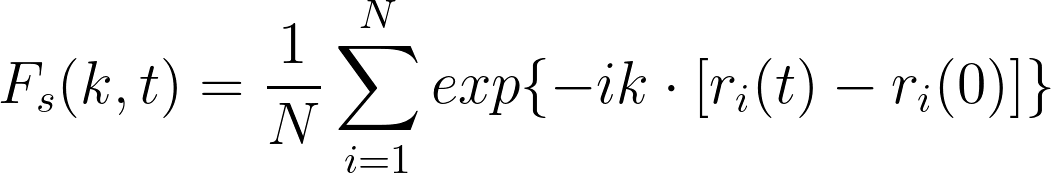
- 验证系统弛豫时间和系统压力的关系
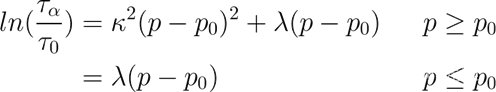
结果
通过收集大量系统模拟分子坐标的实时数据以及对其进行延伸计算,我们可以发现DF Theory是适用于binary hard disk system。
激发识别
用指示函数量化激发的总密度
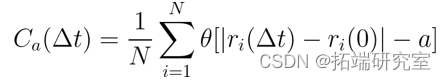
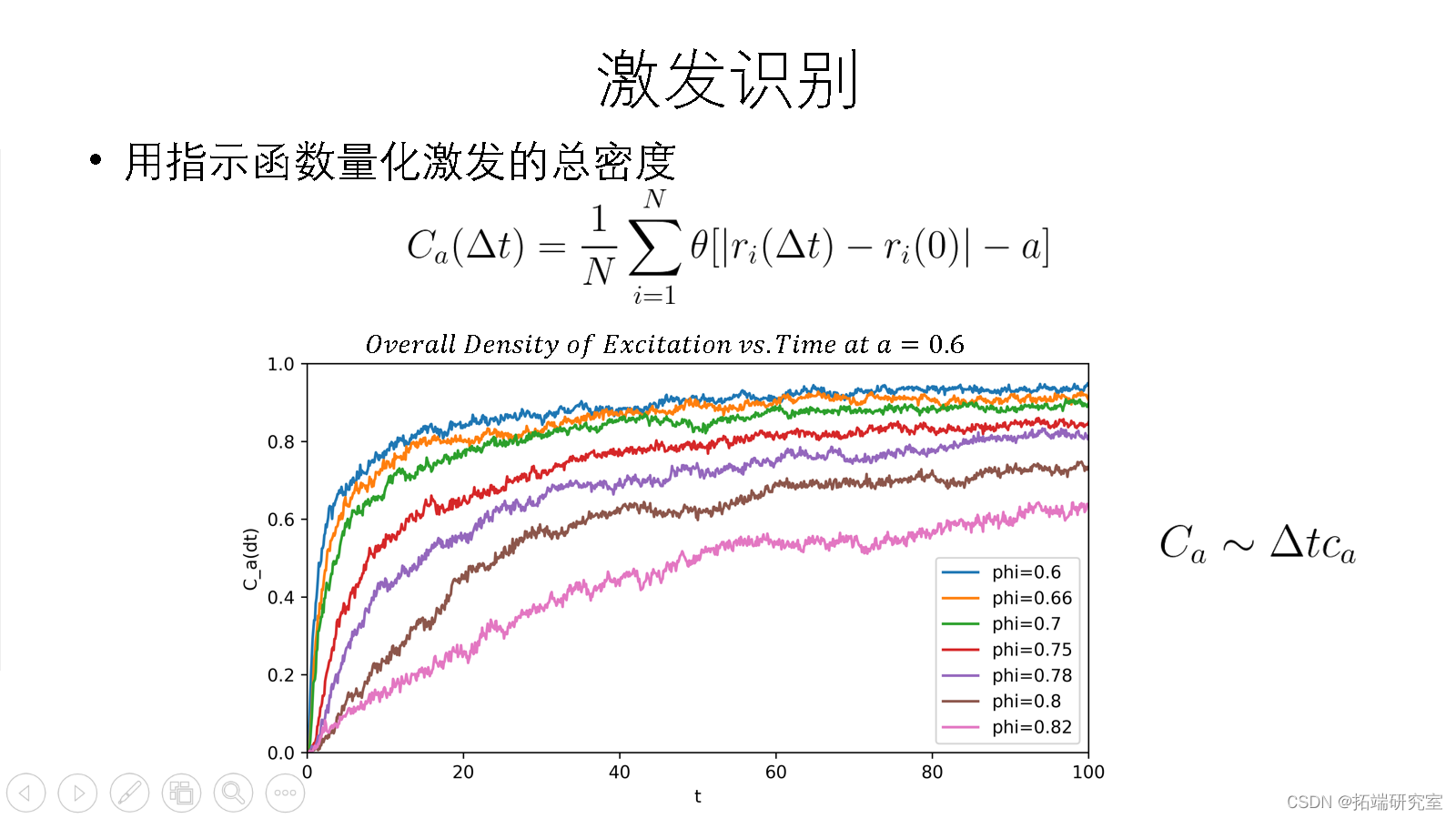
来源:项目PPT
Boltzmann关系:线性关系与查找能量标度KA
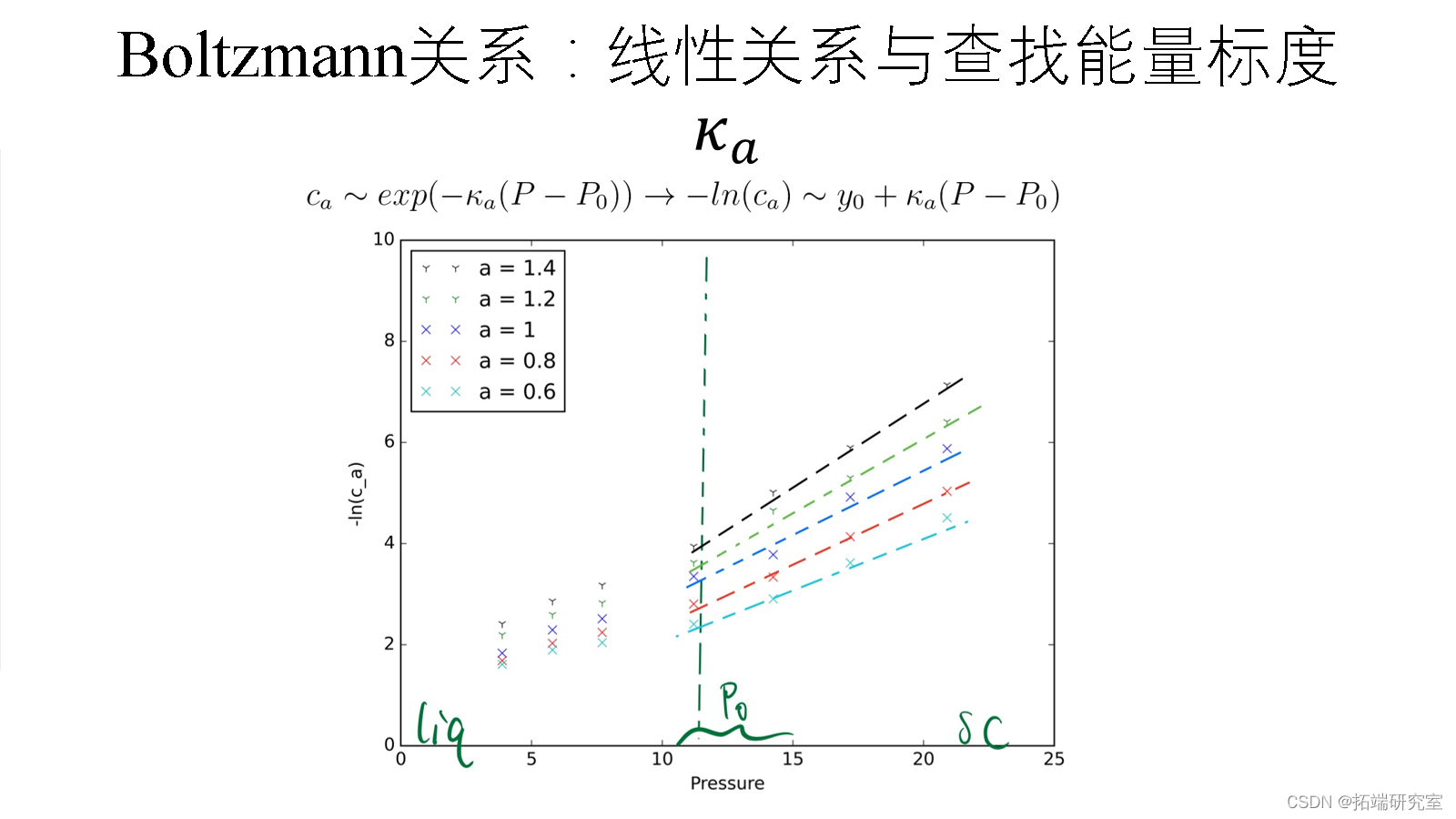
来源:项目PPT
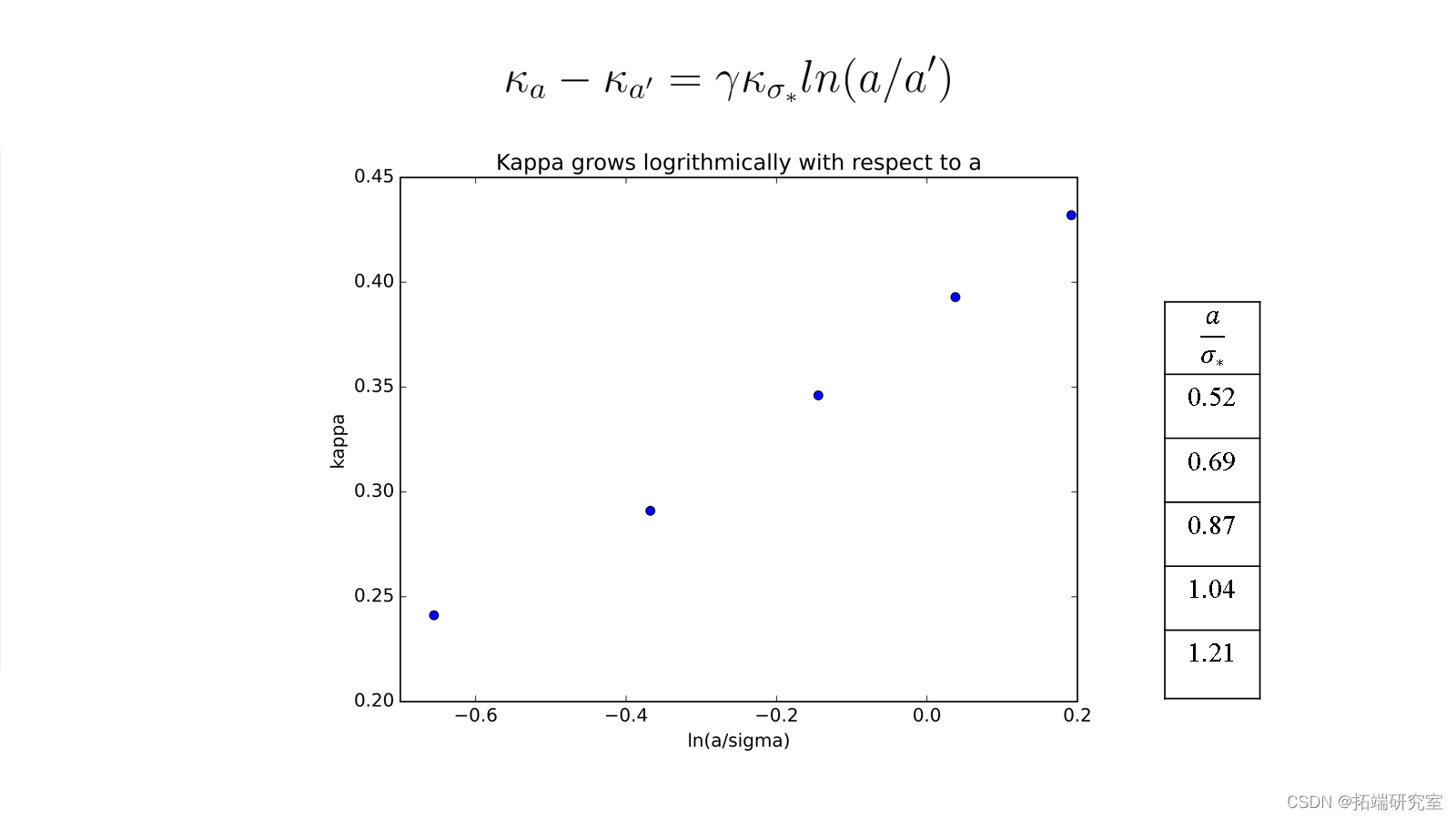
来源:项目PPT
随时关注您喜欢的主题

来源:项目PPT

来源:项目PPT
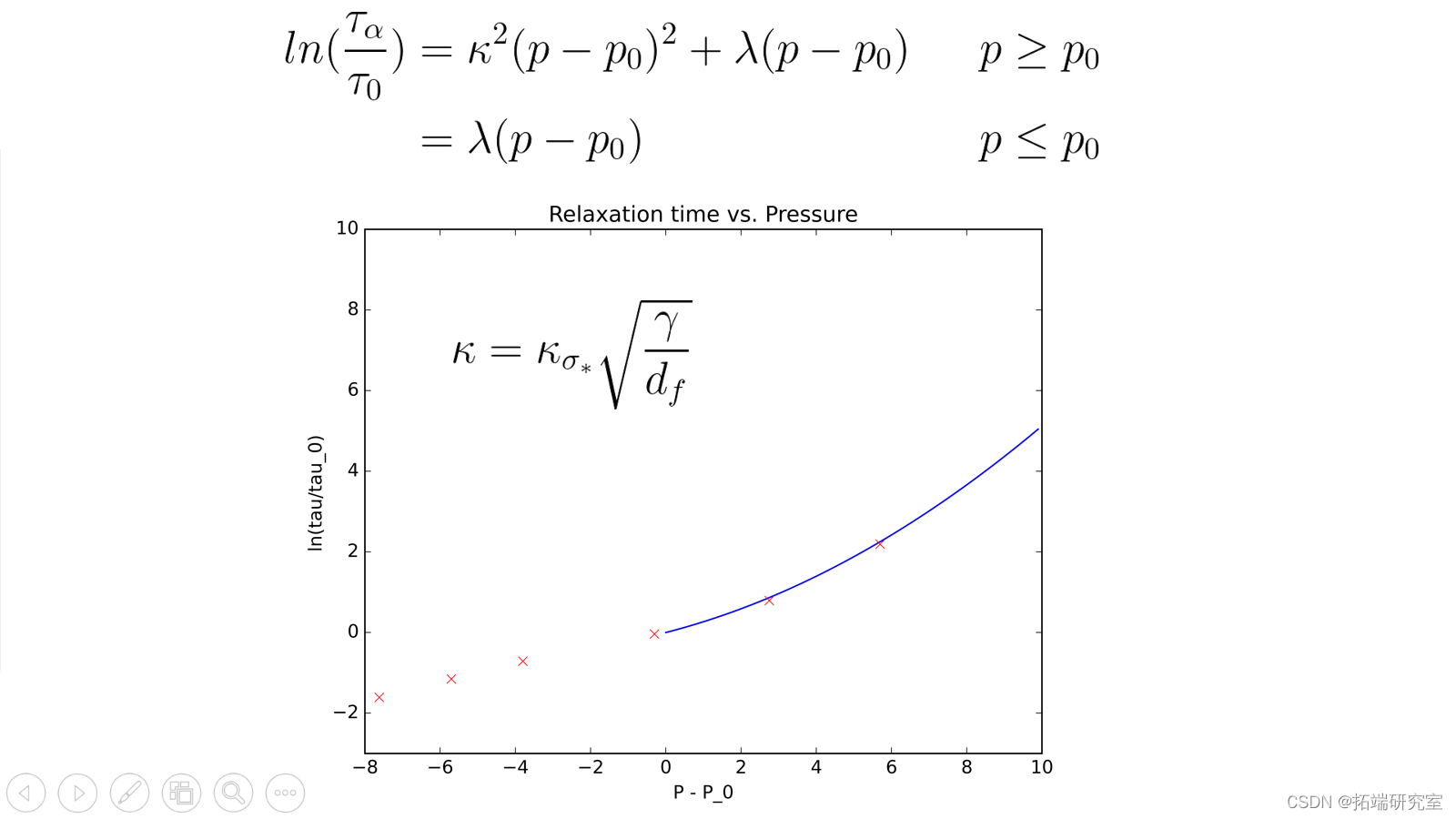
来源:项目PPT

来源:项目PPT
关于作者

Lawrence Xi
在此对Lawrence Xi对本文所作的贡献表示诚挚感谢,他毕业于加州大学圣塔芭芭拉分校,专长化学工程和统计。兴趣技能点广泛,对数据分析,品牌营销,客户策略,以及industry-related科研感兴趣,精通Microsoft Office,Python,Matlab,Mathematica等学术软件,尤其Python 数据分析经验充分。


 Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析
Python蒙特卡罗MCMC:优化Metropolis-Hastings采样策略与Fisher矩阵计算参数推断应用—模拟与真实数据分析 R语言蒙特卡罗Monte Carlo方法进行数值积分和模拟可视化
R语言蒙特卡罗Monte Carlo方法进行数值积分和模拟可视化 R语言布朗运动模拟股市、物种进化树状图、二项分布可视化
R语言布朗运动模拟股市、物种进化树状图、二项分布可视化
